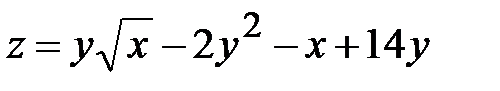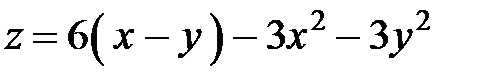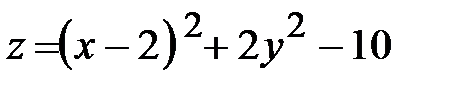Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие неопределенного интеграла.Содержание книги Поиск на нашем сайте
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение Вологодский государственный университет
Кафедра высшей математики
МАТЕМАТИКА Контрольная работа № 2 (2 семестр, 2015-2016 уч. год) Методические указания и контрольные задания для студентов заочной ускоренной формы обучения строительных специальностей
Факультет инженерно-строительный
Вологда
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил:
1. Студент должен выполнять контрольные задания по варианту, в двойном номере которого вторая цифра совпадает с последней цифрой его шифра - номера его зачетной книжки. Если номер заканчивается цифрой 0, то студент должен выполнять вариант №10. 2. Каждая контрольная работа должна быть выполнена в отдельной тетради в клеточку чернилами синего или черного цвета. 3. Образец оформления титульного листа (обложки) тетради приведен на доске объявлений деканата ФЗДО. 4. В работу должны быть включены все задачи, указанные в задании. Работы, содержащие не все задачи задания, а также задачи не своего варианта, не рецензируются. 5. Задачи нужно решать в том порядке, в котором они указаны в контрольной работе. 6. Перед решением каждой задачи надо полностью выписать ее условие. 7. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи (рисунки). 8. Компьютерное оформление работы не рецензируется. 9. Возвращенная прорецензированная незачтенная работа исправляется студентом; исправление записывается в конце работы. Вносить исправления в проверенный текст работы - запрещается.
Введение Настоящие методические указания служат руководством для студентов-заочников при выполнении контрольных заданий, запланированных во 2 учебном семестре. С их помощью студент-заочник сможет самостоятельно разобраться в основных типах задач и справиться с выполнением контрольных заданий. Неопределенный интеграл.
Понятие неопределенного интеграла. Для начала вспомним задачу дифференцирования: дана функция Теперь будем решать обратную задачу: дана функция Определение Функция
Первообразная функция обладает двумя свойствами. Свойство 1. Если какая-то конкретная функция Свойство 2. Пусть найдены две первообразных функции Из этих двух свойств получается важное следствие. Чтобы найти все первообразные функции для функции Фраза «Неопределенный интеграл от функции
функции Запомните термины:
Таблица основных неопределенных интегралов Неопределенные интегралы от основных элементарных функций приведены в следующей таблице.
Теперь сформулируем правила, которые позволяют интегрировать функции, получающиеся из простейших элементарных функций с помощью умножения на число, сложения и вычитания. 1. Постоянный множитель в подынтегральной функции можно выносить за знак интеграла, т.е.
2. Интеграл от суммы или разности функций равен сумме (или, соответственно, разности) интегралов от этих функций, т.е.
К сожалению, нет единых правил для интегрирования произведения и частного функций. Также нет единого правила интегрирования сложной функции. По этой причине приходится признать, что интегрирование функций – операция более сложная, чем дифференцирование.
1.3. Интегрирование с помощью тождественных преобразований подынтегральной функции Пусть требуется найти интеграл Пример 1. Найти неопределенный интеграл Решение. Подынтегральная функция является дробью. В числителе есть разность и сумма функций. Поделим почленно числитель на знаменатель.
Ответ. Пример 2. Найти неопределенный интеграл Решение. В преобразованиях используем формулы тригонометрии.
Ответ. Пример 3. Найти неопределенный интеграл Решение. Перемножим скобки в подынтегральном выражении, чтобы избавиться от произведения.
Ответ. Пример 4. Найти неопределенный интеграл Решение. Нетрудно убедиться, что в таблице такого интеграла нет. Есть интеграл
Преобразуем искомый интеграл с помощью второй формулы.
Ответ.
1.4 Замена переменной (или подведение под знак дифференциала) Сведения из теории Вспомним правило дифференцирования сложной функции. Пусть дана сложная функция Вернемся к задаче интегрирования. Как правило, искомый интеграл всегда дается в виде Вы сами должны увидеть, имеет ли подынтегральная функция структуру Нельзя просто механически заменить символ
Замечание. В учебной литературе этот процесс замены переменной часто называется подведением под знак дифференциала. Поясним смысл этого названия. Пусть увидели в интеграле нужную структуру, т.е.
По определению произведение вида Тогда процесс замены переменной интегрирования будет выглядеть так:
Образно говоря, производная Пример 5. Найти интеграл Решение. Выделим нужную структуру Замена После подстановки в искомый интеграл получаем:
Ответ. Пример 6. Найти интеграл Решение. Единственный табличный интеграл, содержащий показательную функцию, это интеграл
Ответ.
Пример 7. Найти интеграл Решение. Имеем табличный интеграл
Ответ. Пример 8. Найти интеграл Решение. Будем ориентироваться на табличный интеграл:
В нем аргумент синуса и переменная интегрирования должны быть абсолютно одинаковыми. В искомом интеграле изменить аргумент синуса
Ответ. Пример 9. Найти интеграл Решение. В таблице имеем интеграл
Ответ.
Проанализируем полученный результат. Первообразная осталась та же, что и в табличном интеграле – натуральный логарифм модуля. Логарифмируемое выражение совпало со знаменателем в искомом интеграле. Перед первообразной функцией добавился сомножитель, обратный коэффициенту при х.
Все это является проявлением общего правила, полученного на основе замены переменной. Пусть известно, что Из него, в частности, следует расширение таблицы интегралов:
Применение этого правила можно видеть на следующих примерах: 1. 2. 3. 4. 5. 6. 7.
Интегрирование по частям Ранее уже упоминалось, что нет единого правила интегрирования произведения функций. Однако есть метод, который позволяет проинтегрировать некоторые виды произведений. Это метод интегрирования по частям. Его формула имеет вид
Ещё раз подчеркнем, что изначально все интегралы даны в виде При интегрировании по частям нужно выполнить следующие действия: 1) часть подынтегральной функции 2) то, что осталось от подынтегрального выражения, обозначить как дифференциал второй функции
Методические указания: 1. В заготовках при вычислении функции 2. Если подынтегральная функция является произведением многочлена на тригонометрическую функцию или многочлена на показательную функцию, то выгодно взять за функцию 3. Если подынтегральная функция содержит какую-то одну из обратных тригонометрических функций
Пример 10. Найти интеграл Решение.
Пример 11. Найти интеграл Решение.
§2. Определенный интеграл
Понятие определенного интеграла возникло задолго до появления понятий производной, первообразной и неопределенного интеграла. Схема введения этого понятия достаточно проста. Есть функция 1. Этот отрезок произвольным образом разбивается на 2. На каждом таком интервале произвольно выбирается точка 3. Затем строится интегральная сумма 4. Далее разбиение отрезка 5. Последовательность разбиений порождает последовательность интегральных сумм
Вычисление определенного интеграла по определению, т.е. как предел интегральных сумм, задача очень сложная. К счастью, гениальные математики прошлого И.Ньютон и Г.Лейбниц установили связь определенного интеграла с первообразной для функции
Из формулы видно, что достаточно найти какую-то одну первообразную функцию Функции двух переменных
Задания для контрольной работы №2 ЧАСТЬ 1 (задачи 1-5) Задача 1. Найти неопределенные и определенный интегралы.
Задача 2. Найти площадь фигуры, ограниченной графиками заданных функций.
Задача 3. Решить дифференциальные уравнения 1-го порядка.
Задача 4. Решить дифференциальные уравнения 2-го и 3-го порядков. а) Найти частное решение дифференциального уравнения и вычислить значение полученной функции б) Найти общее решение дифференциального уравнения. в) Найти общее решение дифференциального уравнения.
Задача 5. Исследовать на экстремум функцию.
Задания для контрольной работы №2 ЧАСТЬ 2 (задачи 7-10)
Список литературы 1. Пискунов, Н. С. Дифференциальное и интегральное исчисления: учеб. пособие для втузов: [в 2 т.]. Т. 2 / Н. С. Пискунов. - Изд. стер. - Москва: Интеграл-Пресс, 2009. - 544 с. 2. Щипачев, В.С. Высшая математика: учебник для вузов / В.С. Щипачев. – 6-е изд., стер. – Москва: Высш. шк., 2003. – 479 с. 3. Рябушко А. П. Индивидуальные задания по высшей математике: учебное пособие для техн. специальностей вузов: в 4 ч. Ч. 4. Операционное исчисление. Элементы теории устойчивости. Теория вероятностей. Математическая статистика: учеб. пособие / А. П. Рябушко. - 2-е изд., испр. - Минск: Вышэйшая школа, 2007. - 336 с. 4. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и математическая статистика: Учеб. пособие для экон. спец. вузов. – М.: Высш. шк., 1991. – 400 с. 5. Лихолетов И.И., Мацкевич И.П., Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. – Минск: Выш. шк., 1969. – 454 с. 6. Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. – М.: Наука, 1969. – 512 с. 7. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1969. – 576 с. 8. Солодовников А.С. Теория вероятностей. – М.: Просвещение, 1978. 9. Виленкин Н.Я. Индукция, Комбинаторика – М.: Просвещение, 1976. 10. Виленкин Н.Я., Потапов В.Г. Задачник-практикум по теории вероятностей с элементами комбинаторики и математической статистики – М.: Просвещение, 1979. Содержание
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ...2 Введение……………………………………………………………...........……….…...3 §1. Неопределенный интеграл…………………..……..............................…………...3 1.1 Понятие неопределенного интеграла……………………………........…….3 1.2 Таблица основных неопределенных интегралов…………………..............4 1.3 Интегрирование с помощью тождественных преобразований подынтегральной функции...................................................................................................5 1.4 Замена переменной (или подведение под знак дифференциала)...........7 1.5 Интегрирование по частям..................................................................... 11 §2. Определенный интеграл................................................................................. 12 2.1 Методы вычисления определенного интеграла..................................... 13 2.2 Вычисление площадей плоских фигур с помощью определенного интеграла 15 §3. Дифференциальные уравнения 1 – го порядка............................................ 16 3.1. Дифференциальные уравнения с разделенными переменными.......... 17 3.2. Дифференциальные уравнения с разделяющимися переменными..........19 3.3. Линейные дифференциальные уравнения 1-го порядка...................…....21 §4. Дифференциальные уравнения 2– го и 3– го порядков…………………....….24 4.1. Дифференциального уравнения 2 – го и 3 – го порядков, допускающие понижение порядка…………
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.32.243 (0.009 с.) |

 . Найти новую производную функцию
. Найти новую производную функцию  .
. . Нужно найти формулу этой функции
. Нужно найти формулу этой функции  .
. .
. , где
, где  также является первообразной для функции
также является первообразной для функции  и
и  для одной и той же функции
для одной и той же функции  , т.е.
, т.е.  .
. » записывается символами
» записывается символами  . Тогда понятие неопределенного интеграла символьно записывается равенством
. Тогда понятие неопределенного интеграла символьно записывается равенством , где
, где  -- какая - то одна первообразная для
-- какая - то одна первообразная для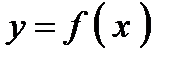 , а
, а  .
.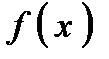 -- подынтегральная функция,
-- подынтегральная функция,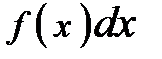 -- подынтегральное выражение,
-- подынтегральное выражение, -- переменная интегрирования.
-- переменная интегрирования.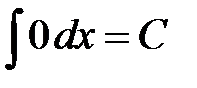

 , если
, если  .
.








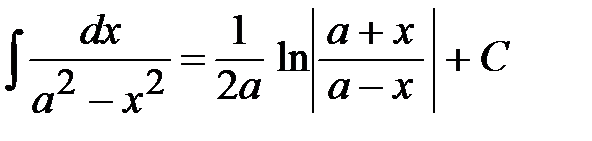






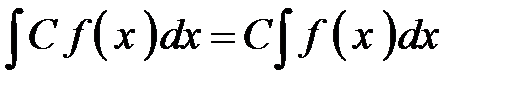 .
. .
.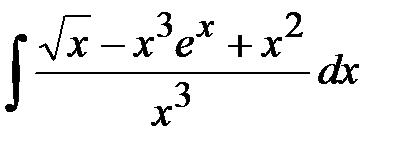 .
.

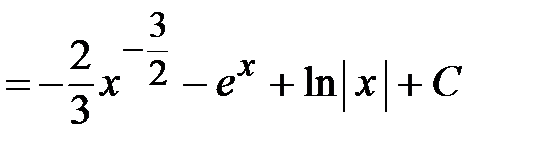 .
. .
.
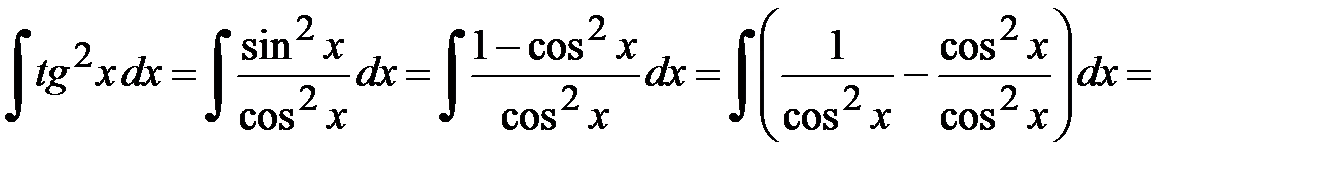

 .
. .
.


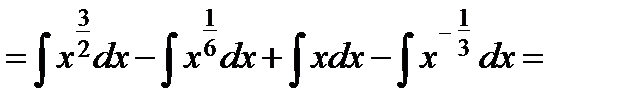


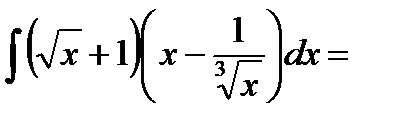

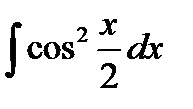 .
. , т.е. от косинуса в первой степени. Поэтому полезно вспомнить две тригонометрические формулы понижения степени.
, т.е. от косинуса в первой степени. Поэтому полезно вспомнить две тригонометрические формулы понижения степени. и
и 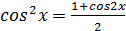 .
.
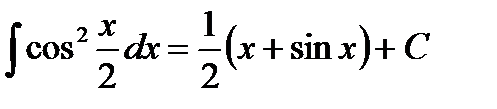
 . Ее производная функция вычисляется по формуле
. Ее производная функция вычисляется по формуле  . Из формулы видно, что сначала вычисляется производная внешней функции
. Из формулы видно, что сначала вычисляется производная внешней функции 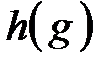 , а потом эта производная умножается на производную внутренней функции
, а потом эта производная умножается на производную внутренней функции 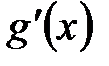 .
.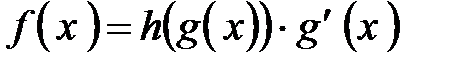 или, хотя бы, близкую к ней. Если Вы эту структуру увидели, то Вы поняли, какую формулу имеет внутренняя функция
или, хотя бы, близкую к ней. Если Вы эту структуру увидели, то Вы поняли, какую формулу имеет внутренняя функция 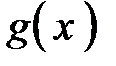 . После этого Вы обозначаете внутреннюю функцию как новую переменную
. После этого Вы обозначаете внутреннюю функцию как новую переменную 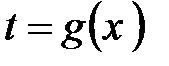 . Тогда
. Тогда  .
.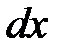 на символ
на символ 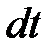 . Предварительно найдем дифференциал новой переменной
. Предварительно найдем дифференциал новой переменной  :
:  . Теперь в исходном интеграле можно перейти к новой переменной интегрирования.
. Теперь в исходном интеграле можно перейти к новой переменной интегрирования. .
.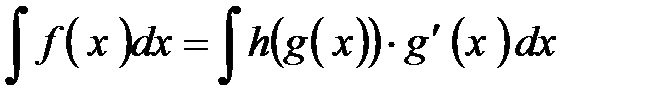 .
. равно дифференциалу функции
равно дифференциалу функции  , т.е.
, т.е.  .
.
 перемещается вправо за символ
перемещается вправо за символ  , превращаясь при этом в свою первообразную
, превращаясь при этом в свою первообразную  . В этом и заключается подведение под знак дифференциала.
. В этом и заключается подведение под знак дифференциала. .
. .
.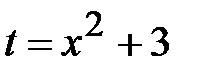 . Заготовка
. Заготовка  .
. .
. .
. .
. . Чтобы прийти к нему, сделаем замену
. Чтобы прийти к нему, сделаем замену  . Вычислим
. Вычислим  . Подставим в искомый интеграл:
. Подставим в искомый интеграл: .
.
 .
. . Подготовим
. Подготовим 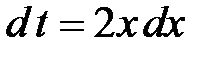 . После подстановки в искомый интеграл получим
. После подстановки в искомый интеграл получим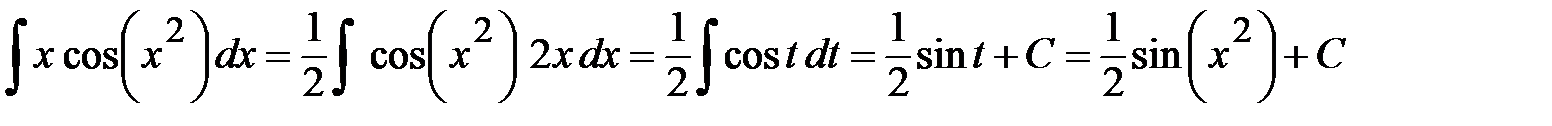 .
. .
. .
. .
. мы не можем. Значит, надо сделать так, чтобы переменной интегрирования стал
мы не можем. Значит, надо сделать так, чтобы переменной интегрирования стал  :
: 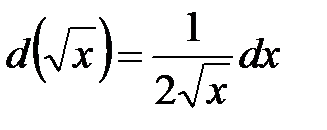 . В искомом интеграле умножим числитель и знаменатель на 2 и выполним цепочку преобразований:
. В искомом интеграле умножим числитель и знаменатель на 2 и выполним цепочку преобразований:
 .
. .
. . Попытаемся искомый интеграл свести к данному табличному. Не будем изменять знаменатель. Сделаем замену переменной, обозначив
. Попытаемся искомый интеграл свести к данному табличному. Не будем изменять знаменатель. Сделаем замену переменной, обозначив  . Вычислим формулу, выражающую дифференциал новой переменной t через дифференциал старой переменной х:
. Вычислим формулу, выражающую дифференциал новой переменной t через дифференциал старой переменной х:  . Тогда
. Тогда  . Подставим все заготовки в искомый интеграл.
. Подставим все заготовки в искомый интеграл.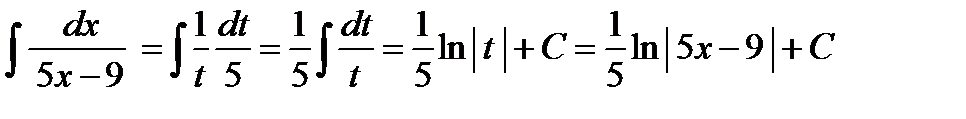
 .
. (как правило, из таблицы интегралов). Тогда
(как правило, из таблицы интегралов). Тогда  .
. ,
если
,
если 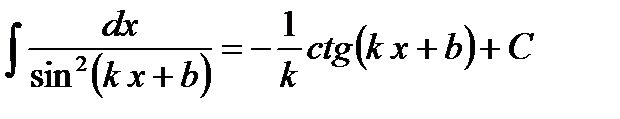
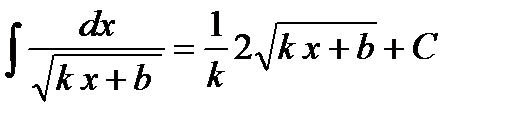


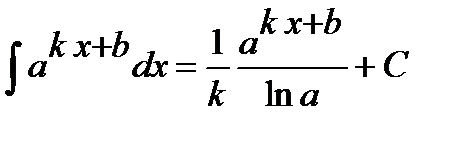

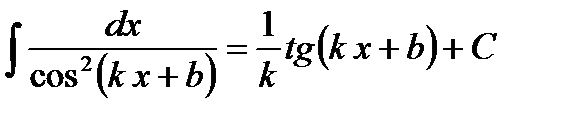




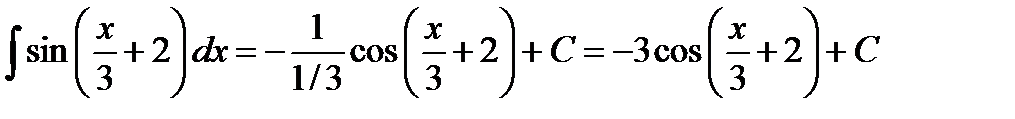




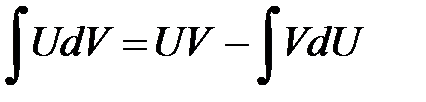 .
. обозначить как новую функцию
обозначить как новую функцию  и приготовить заготовку
и приготовить заготовку  ;
; (которая, вообще-то, изначально неизвестна) и найти эту функцию по формуле
(которая, вообще-то, изначально неизвестна) и найти эту функцию по формуле .
. в неопределенном интеграле берем константу
в неопределенном интеграле берем константу  .
. именно многочлен, т.к. он при дифференцировании упрощается. Тригонометрические и показательные функции не упростятся, сколько бы их ни дифференцировали или интегрировали.
именно многочлен, т.к. он при дифференцировании упрощается. Тригонометрические и показательные функции не упростятся, сколько бы их ни дифференцировали или интегрировали. или логарифмическую функцию
или логарифмическую функцию  , то выгодно именно их выбрать в качестве функции
, то выгодно именно их выбрать в качестве функции  , т.к. известно, как их дифференцировать.
, т.к. известно, как их дифференцировать.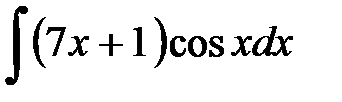 .
.
 .
. .
.
 .
. .
. интервалов
интервалов 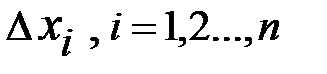 .
.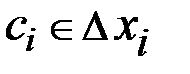 . В ней вычисляется значение функции
. В ней вычисляется значение функции  .
. .
. возрастает, т.е.
возрастает, т.е. 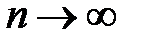 .
. . Если эта последовательность стремится к конечному пределу, то он и называется определенным интегралом. Символически это записывается так
. Если эта последовательность стремится к конечному пределу, то он и называется определенным интегралом. Символически это записывается так .
. . Созданная ими формула известна всему образованному человечеству как формула Ньютона-Лейбница. Она имеет вид
. Созданная ими формула известна всему образованному человечеству как формула Ньютона-Лейбница. Она имеет вид .
.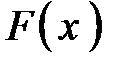 для функции
для функции  . Тогда её приращение
. Тогда её приращение  и будет равно определенному интегралу.
и будет равно определенному интегралу.


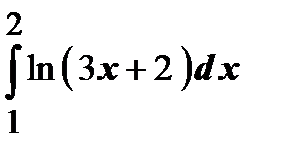





 ;
;






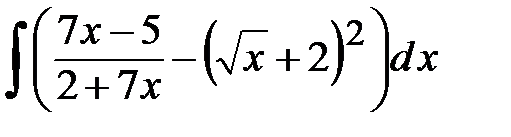




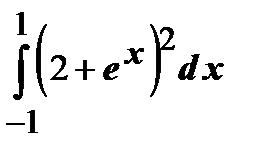
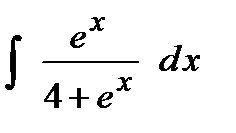



 ;
;

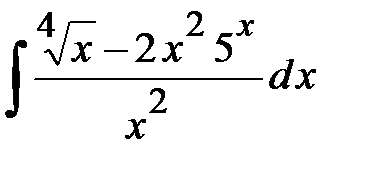
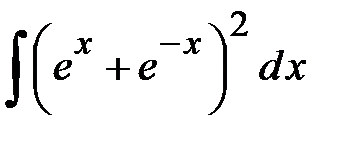

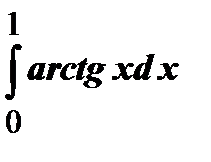



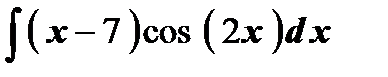




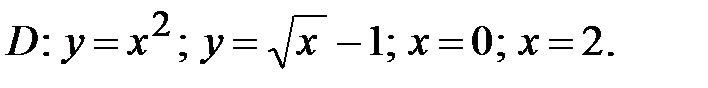





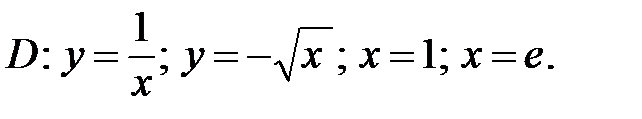

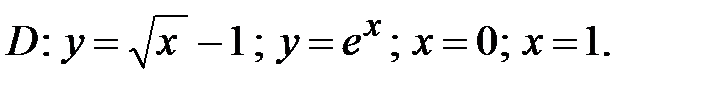


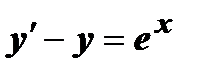 ;
; 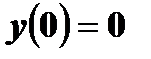 ;
;
 ;
;
 ;
; 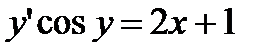 ;
;
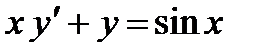 ;
; 
 ;
;
 ;
; 
 ;
;
 ;
; 
 ;
;
 ;
;  ;
;
 ;
; 
 ;
;
 ;
; 
 ;
;
 ;
; 
 ;
;
 ;
; 
 при
при  с точностью до двух знаков после запятой.
с точностью до двух знаков после запятой. ,
,  ,
,  ,
,  ,
, 
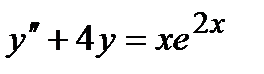 ;
;

 ,
,  ,
,  ,
,  ,
, 
 ;
;

 ,
,  ,
,  ,
,  ,
, 
 ;
;
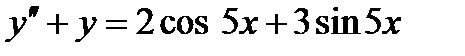
 ;
;  ;
; 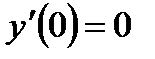 ;
; 


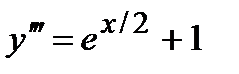 ,
,  ,
,  ,
,  ,
, 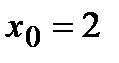

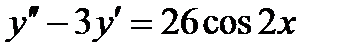
 ;
;  ;
; 
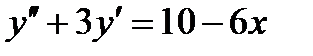

 ;
;  ;
;  ;
; 

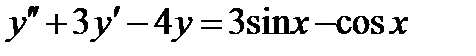
 ,
,  ,
,  ,
,  ,
, 


 ,
, 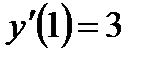 ,
, 

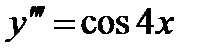 ;
;  ,
,  ,
,  ,
,  .
.