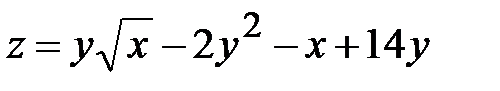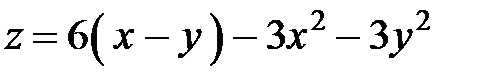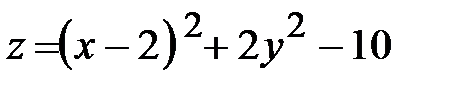Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстремумы функции двух переменныхСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Сведения из теории Напомним, что экстремумы бывают двух типов - максимумы и минимумы. Экстремумы характеризуют функцию локально, только в окрестности некоторой точки. Это вытекает из самого определения экстремума. Определение. Говорят, что функция двух переменных Доказано, что функция Теорема (достаточные условия экстремума) Пусть в точке 1) если 2) если 3) если Пример 30. Исследовать на экстремумы функцию Решение. Прежде всего, найдем точки, в которыхчастные производные Далее найдем формулы частных производных 2-го порядка.
Сначала исследуем достаточные условия для точки
Вычислим Теперь исследуем достаточные условия для точки
Вычислим
Ответ.
Задания для контрольной работы №2 ЧАСТЬ 1 (задачи 1-5) Задача 1. Найти неопределенные и определенный интегралы.
Задача 2. Найти площадь фигуры, ограниченной графиками заданных функций.
Задача 3. Решить дифференциальные уравнения 1-го порядка.
Задача 4. Решить дифференциальные уравнения 2-го и 3-го порядков. а) Найти частное решение дифференциального уравнения и вычислить значение полученной функции б) Найти общее решение дифференциального уравнения. в) Найти общее решение дифференциального уравнения.
Задача 5. Исследовать на экстремум функцию.
Задания для контрольной работы №2 ЧАСТЬ 2 (задачи 7-10)
Задача 7. Решить задачи, используя правила и формулы комбинаторики.
7.1 В автомашине 5 мест. Сколькими способами 5 человек могут разместиться в этой машине, если водительское место могут занять трое из них? 7.2 В комнате имеется 6 лампочек, каждая со своим выключателем. Сколькими способами можно освещать комнату? 7.3 Сколько сигналов можно поднять, имея 4 флага разных цветов, если каждый сигнал должен состоять не менее, чем из двух флагов? 7.4 Сколько различных четырехзначных чисел, делящихся на 4, можно составить из цифр 1, 2, 3, 4 и 5, если цифры в записи могут повторяться? 7.5 Сколькими способами можно выбрать из натуральных чисел от 1 до 30 три числа так, чтобы их сумма была чётной? 7.6 Учащемуся необходимо сдать 4 экзамена на протяжении 8 дней. Сколькими способами это можно сделать? 7.7 В классе изучают 10 предметов. В понедельник 6 уроков, причем все уроки разные. Сколькими способами можно составить расписание на понедельник? 7.8 В депо три локомотива и 7 вагонов. Сколько всего вариантов поезда из 1 локомотива и 5 вагонов можно составить, если локомотив может находиться как в начале, так и в конце поезда? 7.9 На собрании присутствуют 120 человек. Сколькими способами может быть избран президиум собрания в составе председателя, секретаря и семи других членов президиума?
7.10 Бригада состоит из 7 мужчин и 5 женщин. Сколькими способами эта бригада может избрать делегацию в составе пяти человек, среди которых: а) две женщины; б) не более двух женщин?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 502; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.85.59 (0.01 с.) |

 имеет максимум (минимум) в точке
имеет максимум (минимум) в точке 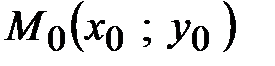 , если существует окрестность этой точки, для всех точек
, если существует окрестность этой точки, для всех точек  которой выполняется неравенство
которой выполняется неравенство  (соответственно для минимума
(соответственно для минимума  ).
). и
и  или эти частные производные не существуют. Известно также, что условие
или эти частные производные не существуют. Известно также, что условие  еще не гарантирует наличие экстремума в точке
еще не гарантирует наличие экстремума в точке  или эти частные производные не существуют. Вычислим для этой точки три числа:
или эти частные производные не существуют. Вычислим для этой точки три числа:  . По ним вычислим выражение
. По ним вычислим выражение  . Тогда:
. Тогда: , то экстремум есть, при этом, если число
, то экстремум есть, при этом, если число  , то минимум, а если
, то минимум, а если 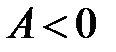 , то максимум;
, то максимум; , то экстремума нет;
, то экстремума нет; , для исследования функции на экстремум нужны дополнительные исследования с использованием частных производных более высокого порядка.
, для исследования функции на экстремум нужны дополнительные исследования с использованием частных производных более высокого порядка. .
. и
и  равны нулю:
равны нулю:  . Система имеет два решения
. Система имеет два решения  и
и  .
. .
. .
. , следовательно, в точке
, следовательно, в точке  .
. , следовательно, в точке
, следовательно, в точке 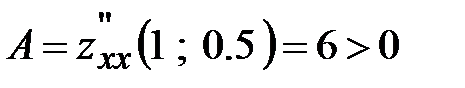 , то минимум. Вычислим его
, то минимум. Вычислим его .
. .
.


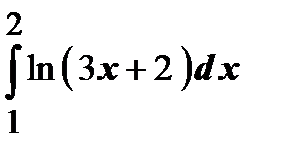





 ;
;






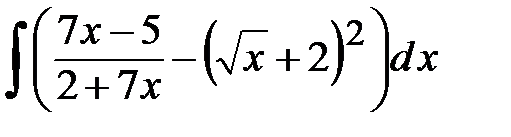




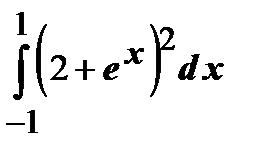
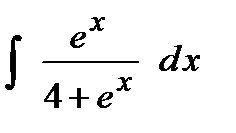



 ;
;

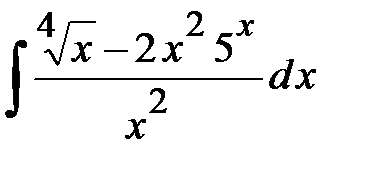
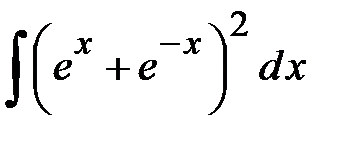

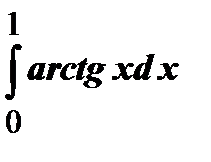



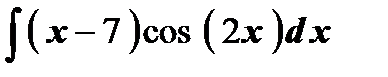




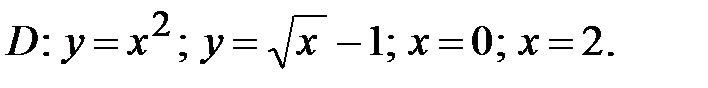





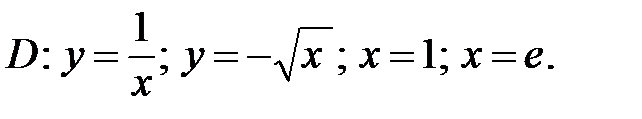

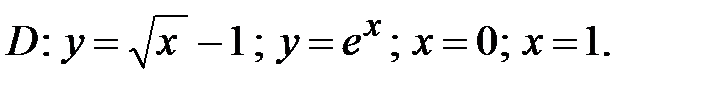


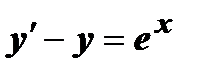 ;
; 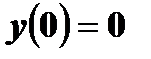 ;
;
 ;
;
 ;
; 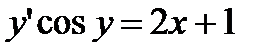 ;
;
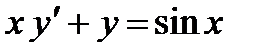 ;
; 
 ;
;
 ;
; 
 ;
;
 ;
; 
 ;
;
 ;
;  ;
;
 ;
; 
 ;
;
 ;
; 
 ;
;
 ;
; 
 ;
;
 ;
; 
 при
при  с точностью до двух знаков после запятой.
с точностью до двух знаков после запятой. ,
,  ,
,  ,
,  ,
, 
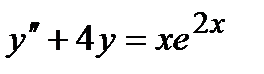 ;
;

 ,
,  ,
,  ,
,  ,
, 
 ;
;

 ,
,  ,
,  ,
,  ,
, 
 ;
;
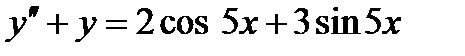
 ;
;  ;
; 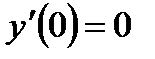 ;
; 


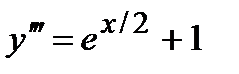 ,
,  ,
,  ,
,  ,
, 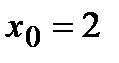

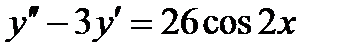
 ;
;  ;
; 
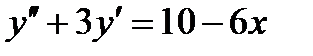

 ;
;  ;
;  ;
; 

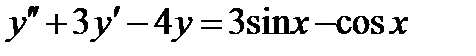
 ,
,  ,
,  ,
,  ,
, 


 ,
, 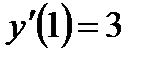 ,
, 

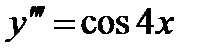 ;
;  ,
,  ,
,  ,
,  .
.