
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства неопределенных интеграловСодержание книги Поиск на нашем сайте Рассмотрим простейшие свойства неопределенного интеграла, которые позволят интегрировать не только основные элементарные функции. 1. Производная от неопределенного интеграла равна подынтегральной функции:
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
3. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной:
Пример 1. Пример 2. 4. Постоянный множитель можно выносить за знак интеграла:
Пример 3. 5. Интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций:
Пример 4.
Формула интегрирования остается справедливой, если переменная интегрирования является функцией: если
Пример 5.
Сравнить с В интегральном исчислении нет универсального способа интегрирования. Применение различных методов приводит данный интеграл к табличному, который надо узнать с учетом свойства инвариантности. Полезно прочитать табличный интеграл, обращая внимание на то, где находится переменная интегрирования (в показателе степени, в знаменателе, под знаком синуса и т. д.).
Методы интегрирования Непосредственное интегрирование Этот метод заключается в прямом использовании табличных интегралов и свойств. Пример. Метод разложения Этот метод заключается в разложении подынтегральной функции в линейную комбинацию более простых функций с использованием известных формул. Пример.
Метод подведения под знак дифференциала Для приведения данного интеграла к табличному бывает удобно сделать преобразования дифференциала. а) Подведение под знак дифференциала линейной функции d(ах+b) = а dх,отсюда dх = dх = d(х + b), dх = Пример.
б) Подведение под знак дифференциала основных элементарных функций: ex dx = d(ex), cos x dx = d(sin x), x dx = d(x2)/2 и т. д. Пример.
Метод замены переменной Существуют две формулы замены переменной в неопределенном интеграле: 1. 2. Здесь x = φ(t) и t = φ(x) суть монотонные дифференцируемые функции своих переменных. Искусство применения метода состоит, в основном, в выборе функций х = φ(t) или t = φ(x) так, чтобы новые интегралы являлись табличными или сводились к ним. В окончательном ответе следует вернуться к старой переменной. Замечание. Подведение под знак дифференциала является частным случаем замены переменной, так как выполняются те же действия, только не вводится новая переменная. Это производится в уме. Пример.
Здесь следует ввести новую переменную t так, чтобы избавиться от квадратного корня. Положим x+1 = t2, тогда x = t2 – 1, а dx = 2t dt:
Метод интегрирования по частям Дифференциал произведения двух функций определяется формулой Интегрируя это равенство, получим выражение:
Отсюда Применение этого метода предполагает субъективное представление подынтегрального выражения в виде Итак, искусство применения метода интегрирования по частям предполагает умение выделять из подынтегральной функции сомножители u и dυс учетом вышеизложенных требований. Конечно, не все интегралы могут быть найдены этим методом. Пример.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 .
.


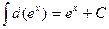




 , то
, то  , где u = φ(x) – произвольная функция, имеющая непрерывную производную. Это свойство называется инвариантностью.
, где u = φ(x) – произвольная функция, имеющая непрерывную производную. Это свойство называется инвариантностью. , поэтому
, поэтому ,
,  .
. .
.
 .
. d (ах + b), а
d (ах + b), а 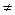 0, в частности
0, в частности .
.
 , где x = φ(t)
, где x = φ(t)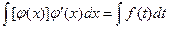 , где φ(x) = t
, где φ(x) = t




 .Это и есть формула интегрирования по частям.
.Это и есть формула интегрирования по частям. ,и при этом интеграл
,и при этом интеграл  должен быть не труднее, чем
должен быть не труднее, чем  . В противном случае применение метода не имеет смысла.
. В противном случае применение метода не имеет смысла.



