
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенные вычисления с помощью дифференциалаСодержание книги Поиск на нашем сайте Теорема. Если функция На этой теореме и основано применение дифференциала к приближенным вычислениям. Известно, что любую из двух эквивалентных бесконечно малых можно приближенно заменить другой. Следовательно, Δy ≈ dy.(9) Абсолютная и относительная погрешности этого равенства могут быть сделаны сколь угодно малыми при достаточно малом
Частные производные и полный дифференциал 5.1. Частные производные. Пусть (x, у) — произвольная фиксированная точка из области определения z = f(x, у). Рассмотрим предел
Этот предел (если он существует) называется частной производной (1-го порядка) данной функции zпо переменной xв точке (x, у). Производная обозначается одним из символов: Аналогично, Частные производные функции z = f(x, у) сами представляют собой некоторые функции переменных x и у. Таким образом, частная производная функции z= f(x, у) по аргументу x есть производная этой функции по x при постоянном значении у. Аналогично, Частные производные функции нескольких переменных определяются как производные этой функции по одному из них при условии, что остальные переменные считаются постоянными.
5.2. Полный дифференциал. Пусть Р(x, у) — данная точка, а Р'(х+Δх, у+Δу)— близкая точка, отвечающая приращениям аргументов Δх и Δу.Полным приращением функции z= f(x, у)в точке Рназывается разность Δz = f(Р') – f(Р) = f(x + Δx, у + Δу) – f(x, у). Если приращение Δzможно представить в виде Δz = АΔх + BΔу + ε,где ε — бесконечно малая более высокого порядка по сравнению с расстоянием ρ = Если функция дифференцируема, то необходимо, чтобы выполнялись равенства: A = Достаточным условием дифференцируемости является наличие непрерывных частных производных. Так как приращения независимых переменных совпадают с их дифференциалами, т. е. Δx = dx, Δу = dу, то дифференциал функции z= f(x, у) вычисляется по формуле
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 296; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.208.109 (0.008 с.) |

 дифференцируема в точке x, причем f '(x)
дифференцируема в точке x, причем f '(x) 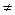 0, то при Δx —> 0 приращение Δy и дифференциал dyфункции являются эквивалентными бесконечно малыми.
0, то при Δx —> 0 приращение Δy и дифференциал dyфункции являются эквивалентными бесконечно малыми. . Структура дифференциала обычно значительно проще структуры приращения функции, в силу чего формула (9) широко применяется в приближенных вычислениях.
. Структура дифференциала обычно значительно проще структуры приращения функции, в силу чего формула (9) широко применяется в приближенных вычислениях.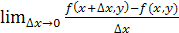 .
.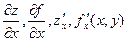 .
.
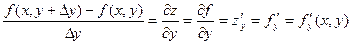 .
. 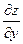 есть производная функции z= f(x, у) по у в предположении, что x является константой.
есть производная функции z= f(x, у) по у в предположении, что x является константой.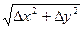 между точками Р и Р' (т.е. ε / ρ —> 0 при ρ —> 0), то функция z= f(x, у) называется дифференцируемой в точке Р, а главная линейная часть ее приращения AΔx + ВΔу = dz называется полным дифференциалом функции в точке Р. Функция, имеющая дифференциал в каждой точке некоторой области D, называется дифференцируемой в этой области.
между точками Р и Р' (т.е. ε / ρ —> 0 при ρ —> 0), то функция z= f(x, у) называется дифференцируемой в точке Р, а главная линейная часть ее приращения AΔx + ВΔу = dz называется полным дифференциалом функции в точке Р. Функция, имеющая дифференциал в каждой точке некоторой области D, называется дифференцируемой в этой области.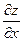 , B =
, B = 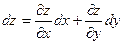 .
.


