
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые приложения дифференциальных уравнений первого порядкаСодержание книги
Поиск на нашем сайте
Задача о радиоактивном распаде Скорость распада Rа (радия) в каждый момент времени пропорциональна его наличной массе. Найти закон радиоактивного распада Rа, если известно, что в начальный момент имелось m0 Rа и период полураспада Rа равен 1590 лет. Решение. Пусть в момент tмасса Rа составляет xг.Тогда скорость распада Rа равна
По условию задачи
где k — коэффициент пропорциональности. Разделяя в последнем уравнении переменные и интегрируя, получим ln x = - kt + lnC, откуда Для определения Сиспользуем начальное условие: при t= 0 x = m0. Тогда С =m0 и, значит, Коэффициент пропорциональности kопределяем из дополнительного условия: при t= 1590 x = m0 /2. Имеем m0 /2= m0е-1590kили е1590k = 2. Отсюда еk = 21/1590 и искомая формула x(t) = m02-t/1590.
Задача о скорости размножения бактерий Скорость размножения бактерий пропорциональна их количеству. В начальный момент имелось 100 бактерий. В течение 3 часов их число удвоилось. Найти зависимость количества бактерий от их количества. Во сколько раз увеличится количество бактерий в течение 9 часов? Решение. Пусть x — количество бактерий в момент t. Тогда согласно условию где k— коэффициент пропорциональности. Отсюда x = cekt. Из условия известно, что х(при t=0) = 100. Значит, С = 100, х = 100еkt. Из дополнительного условия x(при t=3) = 200. Тогда 200 = 100е3k, 2 = е3k, еk = 21/3. Искомая функция: х = 100 ∙2t/3. Значит, при t= 9x = 800, т. е. в течение 9 часов количество бактерий увеличилось в 8 раз. Задача об увеличении количества фермента В культуре пивных дрожжей быстрота прироста действующего фермента пропорциональна его начальному количеству х.Первоначальное количество фермента ав течение часа удвоилось. Найти зависимость x(t). Решение. По условию дифференциальное уравнение процесса имеет вид
отсюда х = сеkt. Но x(при t=0) = a. Значит, С = а,и тогда х = aеkt. Известно также, что х(при t=1) = 2а. Следовательно, 2а = аеk, еk = 2 x(t) = a2t . Задача. Динамика численности популяции Рассмотрим колонию организмов, обитающих в условиях неограниченных ресурсов питания. Предположим, что колония не подавляется никаким другим видом. В силу размножения и смертности число живых организмов в колонии будет меняться с течением времени. Найти закон этого изменения. Решение. Пусть x = x(t) — число живых организмов в момент t, х (t+ Δt) — в момент t + Δt. Тогда Δx = х (t + Δt) – x(t) —приращение функции x(t)за промежуток Δt. Из чего складывается приращение? За время Δtвзрослые особи (или их часть) произведут потомство, а часть особей может погибнуть. Таким образом, Δx = G – H, где G — число развившихся особей за период Δt, H — число погибших особей за это время. Gзависит от длины промежутка Δt(чем больше Δt,тем больше G)и от количества «родителей» (чем больше взрослых особей, тем больше их потомство): G = Ф(x, Δt), где Ф (x, Δt)растет с ростом x или Δtи равна нулю, если равна нулю одна из переменных. Из экспериментов известно, что Δt должна входить линейно: если промежуточные наблюдения увеличить, например, в 2 раза, то и прирост потомства микроорганизмов увеличивается в 2 раза, т.е. Ф(х, Δt) = f (x) Δt. Характер f(x) определить сложнее. Но известно, что f (x) монотонно возрастает с ростом x и f(0) = 0. Но каков рост f (x)? Он существенно зависит от биологических особенностей исследуемого вида, и для его описания могут понадобиться те или иные степени ж, рациональная функция и т. п. Мы рассмотрим простейший случай, когда численность потомства пропорциональна количеству «родителей»: f(x) = αх, α = соnst (например, такой случай реализуется при делении клеток). Итак, G = αх Δt. Аналогично, Н = βx Δt. Следовательно, Δx = γx Δt, (19) где γ = β – α. Разделим обе части равенства (19) на Δtи перейдем к пределу при Δt—» 0:
и, значит,
Тогда, после интегрирования и разделения переменных, будем иметь x(t) = Ceγt. Используем начальное условие: x(t0 ) = x0 (t0 — время начала наблюдения за колонией; x0 — количество организмов). Тогда искомый закон будет иметь такой вид:
Нужно отметить, что найденный закон носит только предположительный пока характер. Для удвоения количества живых организмов требуется всегда одно и то же время, независимо от первоначального количества (кстати, население Земли удваивается примерно через каждые 40 лет).
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 2946; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |


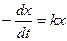
 .
. .
. ,
,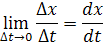
 .
.




