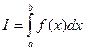Понятие определенного интеграла, свойства

К понятию определенного интеграла приводят разнообраз­ные задачи математики, физики, химии и других точных наук, в том числе вычисление площадей плоских фигур, длин дуг, объема произведенной работы, количества вещества, образовав­шегося в результате химической реакции. Далее рассмотрим некоторые из этих задач более подробно.

Вычисление площади криволинейной трапеции

Криволинейной трапециейбудем называть плоскую фигуру, ограниченную осью ОХ,графиком непрерывной функции у = f(x) и двумя вертикальными прямыми х = а и х = b (рис. 5).

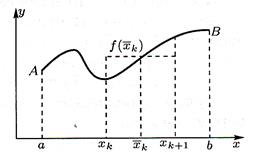
Рис. 5

Чтобы вычислить площадь криволинейной трапеции, проделаем следующие действия. Сначала разделим основание трапеции [а, b]на n частичных интерва­лов [х₀, х₁], [х₁, x₂], …, [х_n-1,х_n],считая что

a = x₀ < x₁ < x₂ < …< x_n-1 < x_n = b

Проведем через точки разбиения прямые, параллельные оси ОУ,тогда фигура аАВbразделится на nэлементарных криво­линейных трапеций. Обозначим Δx_k = х_k+1 – х_k, k = 0,1,..., n – 1.

Вычислим площадь прямоугольника с основанием Δх_kи вы­сотой

,

что приближенно равняется площади k-йэлементарной криволи­нейной трапеции с тем же основанием (см. рис. 5). Учитывая, что площадь фигуры, составленной из нескольких непересекаю­щихся фигур, равна сумме площадей этих фигур, получим

Эта сумма является приближением для искомой площади, причем чем Δх_kменьше (а следовательно, n больше), тем это приближение точнее, т. е.

S = площадь аАВb = lim S_n,

где переход к пределу совершается при условии max Δх_k — > 0.

 

Определенный интеграл. Теорема существования.

Рассмотренный пример, если абстрагироваться от физиче­ского смысла переменных и их обозначений, приводит к одной математической задаче: найти предел интегральной суммы

(10)

при max Δх_k — > 0, где f(x) — функция, непрерывная на промежутке [а, b]. Предел этой суммы называется определенным ин­тегралом от функции f(x) в пределах от aдо bи обозначается

Функция f(x) называется подынтегральной функцией; f(x)dx — подын­тегральным выражением; x — переменной интегрирования: а — нижним, b — верхним пределами интеграла; [а, b]— промежут­ком интегрирования.

Определение. Определенным интегралом называется предел, к которому стремится интегральная сумма (10) при стремлении к нулю длины наибольшего частичного интервала Δх_k.

Теорема (существования определенного интеграла). Если функция f(x) непрерывна в замкнутом интервале [а, b], то ее n-я интегральная сумма стремится к пределу при стремлении к ну­лю наибольшего частичного интервала. Этот предел не зависит от способа разбиения интервала интегрирования на частичные интервалы и от выбора в них промежуточных точек.