
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая и механическая интерпретации производнойСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ЛЕКЦИЯ №1 Тема: Основы математического анализа План: 1. Понятие производной функции 2. Правила дифференцирования функции 3. Понятие дифференциала функции 4. Приближенные вычисления с помощью дифференциала 5. Частные производные и полный дифференциал 6. Понятие неопределенного интеграла, свойства 7. Методы интегрирования 8. Понятие определенного интеграла, свойства 9. Дифференциальные уравнения
Понятие производной функции Рассмотрим функцию Пусть xoи x – два произвольных значения из этого интервала. Обозначим x – xo = Δx, откуда x = хo + Δx. Говорят, что для перехода от значения аргумента хo к значению xпервоначальному значению придано приращение Δx. Приращением Δy функции Δy = f(xo + Δx) – f(хo). (1)
Рис. 1 Пусть Определение. Если существует у'х = Если предел (2) конечен, то производная называется конечной,если же этот предел бесконечен, то у'х — бесконечная производная. Если конечная производная существует в каждой точке некоторого множества, то она оказывается функцией от x, заданной на этом множестве. Правила дифференцирования 1. Производная от постоянной величины равна нулю, т. е. C'= 0. (3) 2. Производная алгебраической суммы конечного числа (u + v + w +...)' = u' + v' + w' +... (3) 3. Производная произведения двух функций определяется (u ∙ v)' = u' ∙ v + u ∙ v' (4) 4. Производная частного от деления двух функций опреде
Пример 1. Найти производную функции Используя таблицу производных, получаем:
Пример 2. Найти производную функции y = x ∙ sinx. Используя правило дифференцирования произведения, получим:
Производные основных элементарных функций
Методы интегрирования Непосредственное интегрирование Этот метод заключается в прямом использовании табличных интегралов и свойств. Пример. Метод разложения Этот метод заключается в разложении подынтегральной функции в линейную комбинацию более простых функций с использованием известных формул. Пример.
Метод подведения под знак дифференциала Для приведения данного интеграла к табличному бывает удобно сделать преобразования дифференциала. а) Подведение под знак дифференциала линейной функции d(ах+b) = а dх,отсюда dх = dх = d(х + b), dх = Пример.
б) Подведение под знак дифференциала основных элементарных функций: ex dx = d(ex), cos x dx = d(sin x), x dx = d(x2)/2 и т. д. Пример.
Метод замены переменной Существуют две формулы замены переменной в неопределенном интеграле: 1. 2. Здесь x = φ(t) и t = φ(x) суть монотонные дифференцируемые функции своих переменных. Искусство применения метода состоит, в основном, в выборе функций х = φ(t) или t = φ(x) так, чтобы новые интегралы являлись табличными или сводились к ним. В окончательном ответе следует вернуться к старой переменной. Замечание. Подведение под знак дифференциала является частным случаем замены переменной, так как выполняются те же действия, только не вводится новая переменная. Это производится в уме. Пример.
Здесь следует ввести новую переменную t так, чтобы избавиться от квадратного корня. Положим x+1 = t2, тогда x = t2 – 1, а dx = 2t dt:
Метод интегрирования по частям Дифференциал произведения двух функций определяется формулой Интегрируя это равенство, получим выражение:
Отсюда Применение этого метода предполагает субъективное представление подынтегрального выражения в виде Итак, искусство применения метода интегрирования по частям предполагает умение выделять из подынтегральной функции сомножители u и dυс учетом вышеизложенных требований. Конечно, не все интегралы могут быть найдены этим методом. Пример.
Формула Ньютона-Лейбница Непосредственное вычисление интеграла как предела соответствующих интегральных сумм затруднительно, да и не требуется, поскольку для этой цели можно воспользоваться следующей теоремой. Теорема. Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятых при верхнем и нижнем пределах интеграла:
Равенство (11) называется формулой Ньютона-Лейбница. Разность значений функции часто записывают так:
В случае использования (12) формуле можно придать вид
Формула Ньютона-Лейбница дает нам альтернативный способ вычисления определенных интегралов. Она позволяет находить их по формуле
Дифференциальные уравнения Основные понятия и определения. При решении различных задач математики и физики, биологии и медицины довольно часто не удается сразу установить функциональную зависимость в виде формулы, связывающей переменные величины, которые описывают исследуемый процесс. Обычно приходится использовать уравнения, содержащие, кроме независимой переменной и неизвестной функции, еще и ее производные. Определение. Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные различных порядков, называется дифференциальным. Неизвестную функцию обычно обозначают у(х)или просто у, а ее производные — у', у"и т. д. Возможны и другие обозначения, например: если у = х(t), то х'(t),х"(t)— ее производные, а t — независимая переменная. Определение. Если функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным. Общий вид обыкновенного дифференциального уравнения:
или Функции Fи f могут не содержать некоторых аргументов, но для того чтобы уравнения были дифференциальными, существенно наличие производной. Определение. Порядком дифференциального уравнения называется порядок старшей производной, входящей в него. Например: х2у' – у = 0, у' + sin х = 0 — уравнения первого порядка, а у" + 2у' + 5у = х — уравнение второго порядка. Определение. Решением дифференциального уравнения называется такая функция, которая обращает уравнение в тождество после подстановки этой функции и ее производных в уравнение. При решении дифференциальных уравнений используется операция интегрирования, что связано с появлением произвольной постоянной. Если операция интегрирования применяется nраз, то очевидно, что в решении будет содержаться nпроизвольных постоянных. ЛЕКЦИЯ №1 Тема: Основы математического анализа План: 1. Понятие производной функции 2. Правила дифференцирования функции 3. Понятие дифференциала функции 4. Приближенные вычисления с помощью дифференциала 5. Частные производные и полный дифференциал 6. Понятие неопределенного интеграла, свойства 7. Методы интегрирования 8. Понятие определенного интеграла, свойства 9. Дифференциальные уравнения
Понятие производной функции Рассмотрим функцию Пусть xoи x – два произвольных значения из этого интервала. Обозначим x – xo = Δx, откуда x = хo + Δx. Говорят, что для перехода от значения аргумента хo к значению xпервоначальному значению придано приращение Δx. Приращением Δy функции Δy = f(xo + Δx) – f(хo). (1)
Рис. 1 Пусть Определение. Если существует у'х = Если предел (2) конечен, то производная называется конечной,если же этот предел бесконечен, то у'х — бесконечная производная. Если конечная производная существует в каждой точке некоторого множества, то она оказывается функцией от x, заданной на этом множестве. Геометрическая и механическая интерпретации производной 1. Если x = f(t)есть уравнение прямолинейного движения точки, то производная представляет собой скорость точки в момент времени t. Быстрота протекания физических, химических, биологических и других процессов, например скорость охлаждения тела, скорость химической реакции и т.п., также выражается при помощи производной. Пример. Предположим, что температура тела Тесть убывающая функция времени: Т = f(t). Пусть t — фиксированный момент времени. Если tполучает приращение Δt, температура Tуменьшается на ΔT; тогда отношение ΔT / Δtпредставляет среднюю скорость охлаждения тела. Предел этого отношения при Δt Таким образом, скорость охлаждения тела равна производной температуры тела по времени. 2. Производная f'(х) функции При этом если существует касательная, то существует и производная, и наоборот. Случаю касательной, не параллельной оси
Рис. 2 (а и б – конечные производные в точке М0; в – бесконечная производная в точке М0) ОУ,отвечает конечная производная, параллельной оси ОУ— бесконечная производная (рис. 2).
Правила дифференцирования 1. Производная от постоянной величины равна нулю, т. е. C'= 0. (3) 2. Производная алгебраической суммы конечного числа (u + v + w +...)' = u' + v' + w' +... (3) 3. Производная произведения двух функций определяется (u ∙ v)' = u' ∙ v + u ∙ v' (4) 4. Производная частного от деления двух функций опреде
Пример 1. Найти производную функции Используя таблицу производных, получаем:
Пример 2. Найти производную функции y = x ∙ sinx. Используя правило дифференцирования произведения, получим:
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 476; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.43.200 (0.009 с.) |

 , определенную в интервале [a, b].
, определенную в интервале [a, b].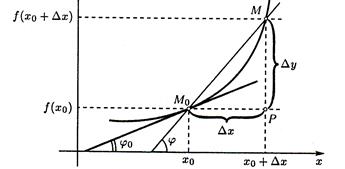

 , то этот предел называется производной от функции
, то этот предел называется производной от функции  или у'х). Итак:
или у'х). Итак: (2)
(2)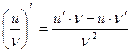 (5)
(5) .
. ,
, 
 .
.



 .
. d (ах + b), а
d (ах + b), а 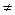 0, в частности
0, в частности .
.
 , где x = φ(t)
, где x = φ(t)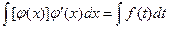 , где φ(x) = t
, где φ(x) = t



 .Это и есть формула интегрирования по частям.
.Это и есть формула интегрирования по частям. ,и при этом интеграл
,и при этом интеграл  должен быть не труднее, чем
должен быть не труднее, чем  . В противном случае применение метода не имеет смысла.
. В противном случае применение метода не имеет смысла.
 , где F`(x) = f(x) (11)
, где F`(x) = f(x) (11) (12)
(12) , где F`(x) = f(x)
, где F`(x) = f(x)

 .
.
 = f '(t)выражает скорость охлаждения тела в данный момент t.
= f '(t)выражает скорость охлаждения тела в данный момент t.



