
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные более высокого порядка
Определение. Производной второго порядка функции Из определения следует, что вторая производная функции является производной от первой производной, то есть
Пример. Вычислим вторую производную функции вая производная
Дифференцирование функции, заданной неявно.
Принято говорить, что равенство
задаёт Пример. Вычислим
Дифференцируя равенство (9) по Выразив из последнего равенства
Можно Дифференцирование функции, заданной параметрически.
Говорят что равенства
задают Для вычисления первой и второй производных Следовательно, производная Окончательные выражения для
Пример. Пусть функция Дифференциал и его свойства
Из определения производной функции
Следовательно, по определению,
Пример. Вычислим дифференциал функции
Перечислим основные свойства дифференциала. 1.
2.
3.
4.
5. Инвариантность формы дифференциала. Если
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ 2
ЗАДАНИЕ 1. Построить график функции
0. 4. 8.
ЗАДАНИЕ 2. Вычислить данные пределы по правилу Лопиталя
0. а) 1. а) 2. а) 3 а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а)
ЗАДАНИЕ 3. Вычислите частные производные второго порядка функций. 0. 3. 6). 8.
ЗАДАНИЕ 4. Дано: функция Требуется: 1) вычислить градиент и производную функции
0. 1. 2. 3. 4. 5. 6. 7. 8. 9.
ЗАДАНИЕ 5. 0. Найдите размеры прямоугольного участка наибольшей площади, который можно огородить забором длины L. 1. Найдите размеры аквариума (без верхней крышки), имеющего форму прямоугольного параллелепипеда объёма V, на изготовление которого требуется наименьшее количество стекла. 2. Для изготовления цилиндрического бака (без верхней крышки) объёма V использовали материалы стоимостью C
3. Найдите размеры ящика (с крышкой), имеющего форму прямоугольного параллелепипеда, наибольшего объёма, который можно изготовить из S м 4. Найдите размеры открытой цилиндрической ванны с полукруглым поперечным сечением и площадью поверхности S м
5. На сфере 6. Найдите размеры прямоугольного параллелепипеда наибольшего объёма, который можно вписать в полушар радиуса R.
7. Найдите размеры прямоугольника (стороны которого параллельны полуосям) наибольшей площади, который можно вписать в эллипс
8. Найдите размеры прямоугольного параллелепипеда наибольшего объёма, который можно вписать в прямой круговой конус высоты h и с радиусом основания r. 9. Найдите размеры прямоугольника с периметром P, который при вращении вокруг одной из своих сторон образует тело наибольшего объёма. ЗАДАНИЕ 6. Вычислите данные неопределённые интегралы.
0. а) 1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а)
ЗАДАНИЕ 7. Вычислите определённые интегралы.
0. а) 1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а)
ЗАДАНИЕ 8. Вычислить несобственные интегралы или установить их расходимость. 0. а) 1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9) а)
ЗАДАНИЕ 9. 0. Найдите площадь фигуры, ограниченной линиями 1. Найдите площадь эллипса
2. Найдите площадь фигуры, ограниченной линиями 3. Найдите площадь фигуры, ограниченной аркой циклоиды
4. Найдите площадь фигуры, ограниченной линией
5. Перейдя к полярным координатам, найдите площадь фигуры, ограниченной линией
6. Найдите длину дуги кривой
8. Найдите объём тела, полученного вращением фигуры
9. Найдите объём эллипсоида
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.159.150 (0.084 с.) |
 в точке
в точке  называют число
называют число 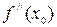 =
=  , если этот предел существует.
, если этот предел существует. =
=  . Аналогично, третья производная является производной от второй производной и т. д.
. Аналогично, третья производная является производной от второй производной и т. д. =
= 
 . Пер-
. Пер-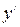 =
=  =
=  =
=  . Вторая производная
. Вторая производная  +
+  =
=  +
+ 
 = =
= =  .
. = 0 (8)
= 0 (8) . Для того, чтобы вычислить производную
. Для того, чтобы вычислить производную  необходимо продифференцировать равенство (8) по переменной
необходимо продифференцировать равенство (8) по переменной  задана следующим уравнением
задана следующим уравнением . (9)
. (9) .
. . Чтобы вычислить вторую производную, дифференцируем последнее равенство по
. Чтобы вычислить вторую производную, дифференцируем последнее равенство по 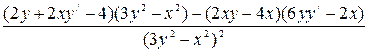 .
. и
и  ,
,  , где
, где  , (10)
, (10) есть время, тогда говорят, что равенства (10) задают закон движения материальной точки на плоскости (так как эти равенства позволяют в каждый момент времени
есть время, тогда говорят, что равенства (10) задают закон движения материальной точки на плоскости (так как эти равенства позволяют в каждый момент времени 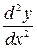 используем тот факт, что дифференциал функции
используем тот факт, что дифференциал функции  .
. =
= 

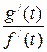 . Аналогично, получим формулу для вычисления второй производной функции
. Аналогично, получим формулу для вычисления второй производной функции  =
=  =
= 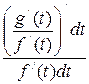 =
=  = =
= =  .
.
 =
=  . Тогда из выведенных формул получим
. Тогда из выведенных формул получим 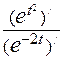 =
= 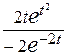 = =
= =  , а производная
, а производная  =
=  = =
= =  =
=  .
. =
= 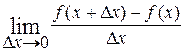 или
или  = 0. Обозначим
= 0. Обозначим  , где
, где  при
при  . Из последнего равенства находим, что
. Из последнего равенства находим, что  =
= 
 +
+ 
 . Обозначив
. Обозначив 
 , где
, где  при
при  является линейной функцией одной переменной
является линейной функцией одной переменной  или кратко
или кратко  .
. , то дифференциал принято записывать в инвариантной форме
, то дифференциал принято записывать в инвариантной форме  .
. при
при  = =
= =  . В точке
. В точке  , а для
, а для  = 0,1 будет
= 0,1 будет  = (3,5)(0,1) = 0,35.
= (3,5)(0,1) = 0,35. , где C – произвольная постоянная.
, где C – произвольная постоянная. .
.
 .
. , тогда, по правилу дифференцирования сложной функции,
, тогда, по правилу дифференцирования сложной функции, 
 =
=  ). Следовательно, форма дифференциала не зависит от того, является ли
). Следовательно, форма дифференциала не зависит от того, является ли  ; 1.
; 1.  ; 2.
; 2. 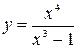 ; 3.
; 3. 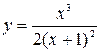 ;
; ; 5.
; 5.  ; 6.
; 6.  ; 7.
; 7.  ;
; ; 9.
; 9.  .
.
 , б)
, б)  ;
; , б)
, б) 
 ;
; , б)
, б)  ;
; , б)
, б)  ;
;
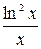 , б)
, б)  ;
; , б)
, б) 
 ;
; , б)
, б)  ;
;
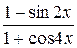 , б)
, б)  ;
; , б)
, б)  ;
;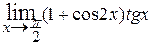 , б)
, б)  .
. ; 1.
; 1.  ; 2.
; 2.  ;
; ; 4.
; 4.  ; 5.
; 5.  ;
; ; 7.
; 7.  ;
; ; 9.
; 9.  .
. , точка
, точка  и вектор
и вектор 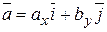 .
. по направлению вектора
по направлению вектора 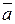 функции в точке
функции в точке  ; 2) составить уравнение касательной плоскости к поверхности
; 2) составить уравнение касательной плоскости к поверхности  ,
, 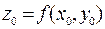 ; 3) найти точки локального экстремума функции
; 3) найти точки локального экстремума функции  ,
,  ;
;
 ,
,  ;
; ,
,  ;
;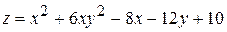
 ;
;
 +
+  ,
, 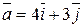 ;
; ,
, 
 +
+  ;
; , М
, М  (1,1),
(1,1),  ;
;

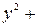 +
+  ,
,  ;
; ,
,  ;
;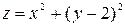 ,
,  .
. (на изготовление дна) и C
(на изготовление дна) и C  (на изготовление боковой стенки) рублей за квадратный метр. Какими должны быть радиус основания и высота бака, чтобы стоимость расходованного материала была наименьшей.
(на изготовление боковой стенки) рублей за квадратный метр. Какими должны быть радиус основания и высота бака, чтобы стоимость расходованного материала была наименьшей. железа.
железа.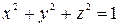 найдите точку, сумма квадратов расстояний которой от двух данных точек A(2,–1,1), B(–1,3,4) была бы наименьшей.
найдите точку, сумма квадратов расстояний которой от двух данных точек A(2,–1,1), B(–1,3,4) была бы наименьшей. .
. , б)
, б)  , в)
, в)  , г)
, г) 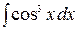 ;
; , б)
, б)  , в)
, в)  , г)
, г)  ;
; , б)
, б)  , в)
, в)  , г)
, г)  ;
; , б)
, б)  , в)
, в) 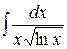 , г)
, г) 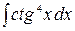 ;
; , б)
, б)  , в)
, в)  , г)
, г)  ;
; , б)
, б)  , в)
, в)  , г)
, г)  ;
; , б)
, б)  , в)
, в)  , г)
, г)  ;
; , б)
, б)  , в)
, в)  , г)
, г) 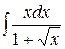 ;
; , б)
, б) 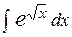 , в)
, в)  , г)
, г)  ;
; , б)
, б) 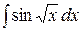 , в)
, в)  , г)
, г)  .
. б)
б) 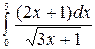 ;
; , б)
, б)  ;
; , б)
, б)  ;
;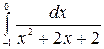 , б)
, б)  ;
; , б)
, б)  ;
; , б)
, б)  ;
; , б)
, б)  ;
; , б)
, б) 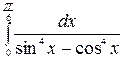 ;
; , б)
, б)  ;
; , б)
, б)  .
. , б)
, б)  ;
; , б)
, б)  ;
; , б)
, б)  ;
; , б)
, б)  ;
; , б)
, б)  ;
; , б)
, б)  ;
; , б)
, б)  ;
;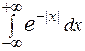 , б)
, б)  ;
; , б)
, б)  ;
;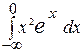 , б)
, б)  .
.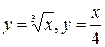 .
. .
. .
. и прямой
и прямой 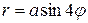 ,
,  .
. .
. . 7). Найдите длину одного витка винтовой линии
. 7). Найдите длину одного витка винтовой линии 

 .
.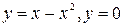 вокруг оси OX.
вокруг оси OX. .
.


