
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойство линейности неопределенного интеграла.Содержание книги
Поиск на нашем сайте
Если
Если имеется постоянный множитель, то он выносится за занк интеграла. 4. Инвариантность неопределенного интеграла. Подведение под знак дифференциала. Всякая формула интегрирования сохраняет свой вид если вместо независимой переменной х подставить диффиренцируемую ф-цию (х), т.е, Если Интегрирование «по частям» в неопределенном интеграле. Рассмотрим функции
Проинтегрировав левую и правую части последнего равенства, получим:
Полученное равенство перепишем в виде:
Замена переменной в неопределенном интеграле. Если в неопределенном интеграле
Виды простейших рациональных дробей. Разложение рациональной дроби на простейшие дроби. 1)Если степень числителя больше степени знаменателя или равна, то в начле выдедяем целую часть, деля числитель на знаменатель. 2)Раскладываем знаменатель на множители. 3)Раскладываем подынтегральную ф-цию на простейшие дроби, с помощью неопределенных коэффицентов (х-а)=
4)находим неопределенные коэфиценты, используя теорему алегебры:Если двамногочлена одинаковой степени тождественно равны, то равно коэффиценты при одинаковых степенях х.
8. Интегралы вида: Интегралы такого вида решаются с помощью формул понижения степени Если степень нечетная, то решается путем разложения ф-ции на множители:
9. Интегралы вида
Интегрирование функций, рационально зависящих от тригонометрических. Универсальная тригонометрическая подстановка.
Задача о площади криволинейной трапеции. Определение определенного интеграла. Тут рисунок криволинейной трапеции. 1.a=X0<X1<X2<Xi-1<Xi<Xn Частичные отрезки 2.ψ1, ψ2, ψi, ψn 3.К каждой из точек ψ nox восстановим перпендикуляр f(ψ1),f(ψ2),f(ψi),f(ψn) 4.На каждом частичном основании построим прямоугольник, высота которого равно f(ψi) Получим ступенчатую фигуру. 5.Найдем ее площадь X1-X0=ΔX1 X2-X1=ΔX2 Xi-Xi-1=ΔXi Xn-Xn-1=ΔXn Sступ фиг= f(ψ1) ΔX1+ f(ψ2) ΔX2+f(ψi) ΔXi+ f(ψn) ΔXn= 6.За истинное значение значения пролощади криволинейной трапеции примем предел к которому стремится записанная сумма, при условии что длины всех частичных отрезков стремят к нулю.
Задача о работе. Определение определенного интеграла. 1.a=X0<X1<X2<Xi-1<Xi<b=Xn частичные отрезки 2. f(ψ1),f(ψ2),f(ψi),f(ψn) 3.Считаем, что на каждом частичном отрезке A=const,ввиду малости длины отрезка и непрерывности функции F 4.Т.к. работа постоянной силы равна произведению величины этой силы на длину перемещения найдем приблизительно А, как суммы всех А А=f(ψ1) ΔX1+ f(ψ2) ΔX2+f(ψi) ΔXi+ f(ψn) ΔXn= 5.За истинное значение примем предел суммы при λ 6.А= Определенный интеграл-это предел последовательности интегральных сумм при условии что длиы всех частичных отрезков стремятся к нулю, и если этот предел существует, и не зависит ни от способа дробления отрезка на частичные, и от выбора точек ψi Теорема существования определенного интеграла. Если ф-ция F(x) непрерывна на отрезке, то определенный интеграл на отрезке ланной ф-ции существует, т.е. существует предел последовательности интегральных сумм и он не зависит ни от способа дробления отрезка, ни от выбора точек ψi Свойства определенного интеграла.
Производная интеграла с переменным верхним пределом. Формула Ньютоно - Лейбница. Ф-ция f(x) непрерывна. x ∈ [a;b]
Если f(x) непрерывна на [a;b], то производная интеграла с переменным верхним пределом равна подынтегральной ф-ции, вычисленной при значении верхнего предела. x+
1.Фиксируем x Ф(x)= 2. x+ 3. 4. 5.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 894; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.0.20 (0.006 с.) |

 и
и  , то
, то  , или
, или
 , то
, то 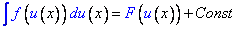
 и
и  , которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:
, которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:


 сделать подстановку
сделать подстановку  , где функция
, где функция  - функция с непрерывной первой производной, то тогда
- функция с непрерывной первой производной, то тогда  , то используя сво-во неопределнного интерграла имеем:
, то используя сво-во неопределнного интерграла имеем:



 такие же интегралы с синусом.
такие же интегралы с синусом. Таким же образом и с cos(x). После разложения пользуемся формулами понижения степени.
Таким же образом и с cos(x). После разложения пользуемся формулами понижения степени.
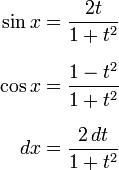





 0
0
 Постоянный множитель можно вынести за знак интеграла
Постоянный множитель можно вынести за знак интеграла Интеграл суммы/разности равен сумме интегралов суммы/разности
Интеграл суммы/разности равен сумме интегралов суммы/разности



 -это ф-ция верхнего предела
-это ф-ция верхнего предела x∈[a;b]
x∈[a;b]
 Ф(x+
Ф(x+ 
 -Ф(x)=
-Ф(x)=  =
= 


 формула Ньютона-Лейбница
формула Ньютона-Лейбница


