Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Балтийский институт экономики и финансовСодержание книги
Поиск на нашем сайте
Балтийский институт экономики и финансов
Методические материалы по курсу «Высшая математика» (Сборник контрольных работ и заданий для самостоятельной работы студентов экономических специальностей)
Калининград 2006
Методические материалы по курсу «Высшая математика» (Сборник контрольных работ и заданий для самостоятельной работы студентов экономических специальностей)- Калининград: БИЭФ, 2006. – с.
Авторы: Карлов А.М., Кикоть Е.Н., Зубарева Н.П. Рецензент: Фунтикова Т.А. кандидат физико-математических наук, доцент кафедры дифференциальной геометрии и топологии РГПУ им. И.Канта, Жарикова Л. кандидат физико-математических наук, доцент кафедры высшей математики БИЭФ
Пособие содержит задания для самостоятельной домашней работы и контрольные работы по основным темам курса высшей математики. Предназначено для текущего контроля знаний студентов.
Для студентов и преподавателей математики.
Ó Балтийский институт экономики и финансов та, 2006
Содержание
Введение ……………………………………………………………….………… I.Задания для самостоятельной работы 1. Зачетное задание №1. Элементы линейной и векторной алгебры, элементы аналитической геометрии ………………………………………… 1.1 Справочный материал………………………………………………….. 1.2. Задания для самостоятельной работы …………………………………. 2. Зачетное задание №2 Предел и непрерывность функции одной переменной. Производная. Исследование функции и построение графика. 2.1 Справочный материал………………………………………………….. 2.2. Задания для самостоятельной работы …………………………………. 3. Зачетное задание №3 Дифференцирование и интегрирование функции нескольких переменных 3.1 Справочный материал………………………………………………….. 3.2. Задания для самостоятельной работы …………………………………. 4. Зачетное задание №4 Интегралы 4.1 Справочный материал………………………………………………….. 4.2. Задания для самостоятельной работы …………………………………. 5. Зачетное задание №5 Дифференциальные уравнения 5.1 Справочный материал………………………………………………….. 5.2. Задания для самостоятельной работы …………………………………. 6. Зачетное задание №6 Числовые и функциональные ряды 6.1 Справочный материал………………………………………………….. 6.2. Задания для самостоятельной работы II. Контрольные работы 1. Контрольная работа №1 Векторная алгебра и аналитическая геометрия………………………………………………………………….. 2. Контрольная работа 2. Предел. Производная…………………….. Контрольная работа №3 Неопределенный и определенный интегралы Контрольная работа №4 Дифференциальные уравнения Список литературы…………………………………………………………
Введение Настоящее пособие содержит методические указания, краткий теоретический материал, индивидуальные задания для самостоятельной работы и контрольные задания по курсу высшей математики. Представлены разделы: «Линейная алгебра и аналитическая геометрия», «Дифференциальное исчисление функции одной и нескольких переменных», «Интегральное исчисление функции одной и нескольких переменных», «Дифференциальные уравнения», «Числовые и степенные ряды».
Зачетное задание №1. Элементы линейной и векторной алгебры, Элементы аналитической геометрии Справочный материал. Исследование системы m линейных уравнений с n переменными.
УМНОЖЕНИЕ ВЕКТОРОВ
УРАВНЕНИЯ ПЛОСКОСТИ
Вывод уравнения плоскости:
2. Задания для самостоятельной работы.
Задание 1. Исследовать данную систему и в случае совместности уравнений системы решить ее методом Гаусса.
Задание 2. Решить данное матричное уравнение.
Задание 3. По координатам точек А, В и С для указанных векторов найти: а) модуль вектора а; б) проекцию вектора с на вектор d; в) координаты точки М, делящей отрезок АВ пополам.
3.1. А(4, 6, 3), В(-5, 2, 6), С(4, -4, -3), а = 4СВ – АС, с = СВ, d = АС. 3.2. А(4, 3, 2), В(-3, -1, 4), С(2, 2, 1), а = -5АС + 2СВ, с = АС, d = СВ. 4.3. А(-2, -2, 4), В(1, 3, -2), С(1, 4, 2), а = 2АС - 3ВА, с = СВ, d = АС. 3.4. А(2, 4, 3), В(3, 1, -4), С(-1, 2, 2), а = 2ВА + 4АС, с = ВА, d = АС. 3.5. А(2, 4, 5), В(1, -2, 3), С(-1, -2, 4), а = 3АВ - 4АС, с = ВС, d = АВ. 3.6. А(-1, -2, 4), В(-1, 3, 5), С(1, 4, 2), а = 3АС – 7ВС, с = АВ, d = АС. 3.7. А(1, 3, 2), В(-2, 4, -1), С(1, 3, -2), а = 2АВ + 5СВ, с = АС, d = АВ. 3.8. А(2, -4, 3), В(-3, -2, 4), С(0, 0, -2), а = 3АС - 4СВ, с = АВ, d = СВ. 3.9. А(3, 4, -4), В(-2, 1, 2), С(2, -3, 1), а = 5СВ + 4АС, с = ВА, d = АС. 3.10. А(0, 2, 5), В(2, -3, 4), С(3, 2, -5), а = -3АВ + 4СВ, с = АС, d = АВ. 3.11. А(-2, -3, -4), В(2, -4, 0), С(1, 4, 5), а = 4АС - 8ВС, с = АВ, d = ВС. 3.12. А(-2, -3, -2), В(1, 4, 2), С(1, -3, 3), а = 2АС - 4ВС, с = АВ, d = АС. 3.13. А(5, 6, 1), В(-2, 4, -1), С(3, -3, 3), а = 3АВ - 4ВС, с = АС, d = АВ. 3.14. А(10, 6, 3), В(-2, 4, 5), С(3, -4, 6), а = 5АС - 2СВ, с = ВА, d = АС. 3.15. А(3, 2, 4), В(-2, 1, 3), С(2, -2, 1), а = 4ВС – 3АС, с = АС, d = ВС. 3.16. А(-2, 3, 4), В(3, -1, 2), С(4, 2, 4), а = 7АС + 4СВ, с = АВ, d = СВ. 3.17. А(4, 5, 3), В(-4, 5, 3), С(5, -6, -2), а = 9АВ - 4ВС, с = АС, d = СВ. 3.18. А(2, 4, 6), В(-3, 5, 1), С(4, -5, 4), а = -6ВС + 2ВА, с = СА, d = ВА. 3.19. А(-4, -2, -5), В(3, 7, 2), С(4, 6, -3), а = 9ВА + 3ВС, с = АС, d = ВС. 3.20. А(5, 4, 4), В(-5, 2, 3), С(4, 2, -5), а = 11АС – 6АВ, с = АВ, d = АС. Задание 4.
4.1 Даны вершины треугольника А(1,-1,2), В(5,-6,2) и С(2,3,-1). Вычислить длину его высоты, проведенной из вершины В на сторону АС. 4.2. Вычислить площадь треугольника с вершинами в точках А(1,3,-1), В(1,-1,3), С(5,-6,2). 4.3. Дана пирамида с вершинами в точках А1(3,1,4), А2(-1,6,1), А3(-1,1,6), А4(0,4,-1). Найти длину высоты, проведенной из вершины А4 на грань А1 А2 А3. 4.4. Найти площадь параллелограмма, построенного на векторах 4.5. Вычислить любую высоту параллелепипеда, построенного на векторах
4.6. Вершины треугольной пирамиды находятся в точках А(0,0,0), В(3,4,-1), С(2,3,5), Д(6,0,-3). Найти длину высоты, проведенной из вершины С. 4.7. Найти вектор 4.8. Найти координаты вектора
4.9. Даны векторы 4.10. Вектор 4.11. Доказать, что точки А(0,1,5), В(2,1,3), С(-1,2,1), Д(1,2,-1) лежат в одной плоскости. 4.12..При каком значении коэффициента 4.13. Найти единичный вектор 4.14. Вершины треугольной пирамиды находятся в точках А(0,0,0), В(3,4,-1), С(2,3,5), Д(6,0,-3). Найти длину высоты, проведенной из вершины А. 4.15. Вычислить высоту параллелепипеда, построенного на векторах 4.16. Найти проекцию вектора 4.17. Дана треугольная пирамида с вершинами А(0,0,1), В(2,3,4), С(6,2,3) и Д(3,7,2). Найти длину высоты пирамиды, проведенной на грань ВСД. 4.18. Дана треугольная пирамида с вершинами А(0,0,1), В(2,3,4), С(6,2,3) и Д(3,7,2). Найти длину высоты пирамиды, проведенной на грань АСД. 4.19. Как расположены точки А(0,1,5), В(2,1,3), С(-1,2,1), Д(1,2,0)? Лежат ли они в одной плоскости? 4.20. Даны векторы
Задание 5. Даны векторы а, в, с: а) вычислить смешанное произведение трех векторов; б) найти модуль векторного произведения; в) вычислить скалярное произведение двух векторов; г) проверить, будут ли коллинеарны или ортогональны два вектора; д) проверить, будут ли компланарны три вектора.
5.1. а = 2 i - 3 j + k, в = j + 4 k, с = 5 i + 2 j -3 k; а) а, 3 в, с; б) 3 а, 2 с; в) –4 с, в; г) а, с; д) а, 2 в, 3 с. 5.2. а = 3 i + 4 j + k, в = i - 2 j + 7 k, с = 3 i -6 j + 21 k; а) 5 а, 2 в, с; б) 4 в, 2 с; в) с, а; г) в, с; д) 2 а, -3 в, с. 5.3. а = 2 i - 4 j - 2 k, в = 7 i + 3 j, с = 3 i + 5 j -7 k; а) а, 2 в, 3 с; б) 3 а, -7 в; в) с, -2 а; г) а, с; д) 3 а, 2 в, 3 с. 5.4. а = -7 i + 2 k, в = 2 i - 6 j + 4 k, с = i - 3 j + 2 k; а) а, -2 в, -7 с; б) 3 с, 4 в; в) -7 с, 2 а; г) в, с; д) 2 а, 4 в, 3 с. 5.5. а = -4 i + 2 j - k, в = 3 i + 5 j - 2 k, с = j + 5 k; а) а, 6 в, 3 с; б) а, 2 в; в) –4 с, а; г) а, в; д) а, 6 в, 3 с. 5.6. а = 3 i - 2 j + k, в = 2j - 3 k, с = -3 i + 2 j - k; а) а, -3 в, 2 с; б) 5 а, 3 с; в) –2 а, в; г) а, с; д) 5 а, 4 в, 3 с. 5.7. а = 4 i - j + 3 k, в = 2 i + 3 j - 5 k, с = 7 i + 2 j + 4 k; а) 7 а, -4 в, 2 с; б) 3 а, 5 с; в) 4 с, 2 в; г) в, с; д) 7 а, 2 в, 5 с. 5.8. а = 4 i + 2 j - 3 k, в = 2 i + k, с = -12 i - 6 j + 9 k; а) 2 а, 3 в, с; б) 4 а, 3 в; в) -4 с, в; г) а, с; д) 2 а, 3 в, -4 с. 5.9. а = - i + 5 k, в = -3 i + 2 j + 2 k, с = -2 i - 4 j + k; а) 3 а, -4 в, 2 с; б) 7 а, -3 с; в) 4 в, 3 а; г) в, с; д) 7 а, 2 в, -3 с. 5.10. а = 6 i - 4 j + 6 k, в = 9 i - 6 j + 9 k, с = i - 8 k; а) 2 а, -4 в, 3 с; б) –9 с, 3 в; в) -5 с, 3 а; г) а, в; д) 3 а, -4 в, -9 с. 5.11. а = 5 i - 3 j + 4 k, в = 2 i - 4 j - 2 k, с = 3 i + 5 j - 7 k; а) а, -4 в, 2 с; б) 4 с, -2 в; в) 6 с, -3 а; г) с, в; д) а, -2 в, 6 с. 5.12. а = -4 i + 3 j - 7 k, в = 4 i + 6 j - 2 k, с = 6 i + 9 j - 3 k; а) -2 а, в, -2 с; б) 7 с, 4 в; в) –3 в, 5 а; г) с, в; д) -2 а, 4 в, 7 с. 5.13. а = -5 i + 2 j - 2 k, в = 7 i - 5 k, с = 2 i + 3 j - 2 k; а) 2 а, 4 в, -5 с; б) 11 с, -3 в; в) –6 с, 8 а; г) с, а; д) 2 а, 4 в, -5 с. 5.14. а = -4 i - 6 j + 2 k, в = 2 i + 3j - k, с = - i + 5 j - 3 k; а) 5 а, 7 в, 2 с; б) 11 а, -4 в; в) –7 с, 3 а; г) в, а; д) 3 а, 7 в, -2 с. 5.15. а = -4 i + 2 j - 3 k, в = - 3j + 5 k, с = 6 i + 6 j - 4 k; а) 5 а, - в, 3 с; б) -7 а, 4 с; в) 9 в, 3 а; г) с, а; д) 3 а, -9 в, 4 с. 5.16. а = -3 i + 8 j, в = 2 i + 3 j - 2 k, с = 8 i + 12 j - 8 k; а) 4 а, -6 в, 5 с; б) -7 а, 9 с; в) 3 в, -8 с; г) с, в; д) 4 а, -6 в, 9 с. 5.17. а = 2 i - 4 j - 2 k, в = -9 i + 2 k, с = 3 i + 5 j - 7 k; а) 7 а, 5 в, - с; б) 5 а, 4 в; в) 3 в, -8 с; г) с, а; д) 7 а, 5 в, - с. 5.18. а = 9 i - 3 j + k, в = 3 i - 15 j + 21 k, с = i - 5 j + 7 k; а) 2 а, -7 в, 3 с; б) -6 а, 4 с; в) 5 в, 7 а; г) с, в; д) 2 а, -7 в, 4 с. 5.19. а = -2 i + 4 j - 3 k, в = 5 i + j - 2 k, с = 7 i + 4 j - k; а) а, -6 в, 2 с; б) –8 в, 2 с; в) 7 с, -9 а; г) а, в; д) а, -6 в, 5 с. 5.20. а = -9 i + 4 j - 5 k, в = i - 2 j + 4 k, с = -5 i + 10 j - 20 k; а) -2 а, 7 в, 5 с; б) –6 в, 7 с; в) 4 с, 9 а; г) с, в; д) -2 а, 7 в, 4 с. 5.21. а = 2 i - 7 j + 5 k, в = -i + 2 j - 6 k, с = 3 i + 2 j - 4 k; а) -3 а, 6 в, - с; б) 5 в, 3 с; в) –4 в, 7 а; г) с, в; д) 7 а, -4 в, 3 с. 5.22. а = 7 i - 4 j - 5 k, в = i - 11 j + 3 k, с = 5 i + 5 j + 3 k; а) 3 а, -7 в, 2 с; б) 2 в, 6 с; в) –4 а, -5 с; г) с, а; д) -4 а, 2 в, 6 с. 5.23. а = 4 i - 6 j - 2 k, в = -2 i + 3 j + k, с = 3 i - 5 j + 7 k; а) 6 а, 3 в, 8 с; б) -7 в, 6 а; в) 4 с, -5 а; г) в, а; д) -5 а, 3 в, 4 с. 5.24. а = 3 i - j + 2 k, в = - i + 5 j - 4 k, с = 6 i - 2 j + 4 k; а) 4 а, -7 в, -2 с; б) –4 с, 6 а; в) 5 в, -2 а; г) с, а; д) 6 а, -7 в, -2 с. 5.25. а = -3 i - j - 5 k, в = 2 i - 4 j + 8 k, с = 3 i + 7 j - k; а) 2 а, - в, 3 с; б) 4 с, -9 а; в) 5 в, -6 с; г) с, в; д) 2 а, 5 в, -6 с.
Задание 6. Прямые на плоскости.
6.1 Найти уравнение прямой, проходящей через точку М(5,0) и точку пересечения прямой 3х-2у+4=0 с осью 0У. 6.2 Написать уравнение прямой, проходящей через точку М(-1,2) параллельно прямой 2х+3у+1=0. 6.3 Дан треугольник с вершинами в точках А(1,1), В(-2,3), С(4,7). Написать уравнение медианы, проведенной из вершины А. 6.4 Даны уравнения сторон треугольника х+2у-1=0, 5х+4у-17=0, х-4у+11=0. Составить уравнение прямой, проходящей через одну из вершин треугольника параллельно противоположной стороне. 6.5 Выяснить, принадлежат ли точки А(-1,2), В(3,4), С(1,2) одной прямой. 6.6 Написать уравнение прямой, проходящей через точку М(4,3) перпендикулярно к вектору 6.7 При каких значениях α прямые α х-2у-1=0 и 6х-4у-3=0: а) параллельны, б) имеют одну общую точку? 6.8 Дан треугольник с вершинами в точках М1(2,5), М2 (-1,3), М3(0,0). Составить уравнение медианы, проведенной из вершины М3. 6.9 Найти расстояние между прямыми 3х-4у+25=0 и 6х-8у-50=0. 6.10 Дан треугольник с вершинами в точках А(1,5), В(-4,3), С(2,9). Найти уравнение высоты, проведенной из вершины А. 6.11 Найти угол между прямыми 5х-3у-2=0 и 3х+5у+1=0. 6.12 Найти уравнение прямой, проходящей через точку А(1,-1) параллельно прямой, соединяющей точки М1(2,-3), М2 (5,1). 6.13 Найти уравнение прямой, проходящей через точку М(-1,3) и точку пересечения прямых 2х-у-1=0, 3х+у-4=0. 6.14 Найти уравнение прямой, проходящей через точку М1(2,3) ортогонально вектору 6.15 На прямой 2х+у+11=0 найти точку, равноудаленную от двух данных точек А(1,1) и В(3,0). 6.16 Найти угол между прямой 2х+3у-1=0 и прямой, проходящей через точки М1(-1,2), М2 (0,3). 6.17 Написать уравнение прямой, проходящей через начало координат перпендикулярно прямой 2х-6у+13=0. 6.18 Дан треугольник с вершинами в точках А(-1,2), В(0,1) и С(1,4). Написать уравнение прямой, проходящей через вершину А параллельно противоположной стороне. 6.19 Найти уравнение прямой, проходящей через точку М1(-1,2), перпендикулярно к прямой, соединяющий точки М2(2,3) и М3(0,-1). 6.20 Даны вершины треугольника А(3,5), В(-3,3), С(5,-8). Определить длину медианы, проведенной из вершины С.
Задание 7. Кривые второго порядка.
7.1. Составить каноническое уравнение эллипса, большая полуось которого равна 10, эксцентриситет 0,6. 7.2. Составить каноническое уравнение гиперболоиды, действительная полуось которой равна 3, а эксцентриситет 7.3. Составить каноническое уравнение эллипса, сумма полуосей которого 8 и расстояние между фокусами 8. 7.4. Вычислить эксцентриситет гиперболы, если угол между ее асимптотами равен 7.5. Эллипс, симметричный относительно осей координат, проходит через точки М(2,3) и В(0,2). Написать уравнение эллипса. 7.6. Составить каноническое уравнение параболы с вершиной в начале координат, симметричной относительно оси 0у, фокус которой находится в точке F(0,-3). 7.7. Составить каноническое уравнение гиперболы, если расстояние между ее фокусами равно 16, а расстояние между вершинами 12. 7.8. Составить уравнение эллипса, проходящего через точку А(4,6), фокусы которого совпадают с фокусами гиперболы х2-у2=8. 7.9. Найти координаты фокусов и эксцентриситет эллипса х2+9у2=81. 7.10. Найти уравнение гиперболы, вершины которой находятся в фокусах, а фокусы – в вершинах эллипса 5х2+8у2=40. 7.11. Составить каноническое уравнение эллипса, если расстояния от одного из фокусов до конца его большой оси равны 7 и 1. 7.12. Написать уравнение гиперболы, если ее асимптоты заданы уравнениями 3х±4у=0, а расстояние между фокусами равно 20. 7.13. Через фокус параболы у2=10х проведена хорда, перпендикулярная к ее оси. Определить длину этой хорды. 7.14. Найти уравнение эллипса, симметричного относительно осей координат и проходящего через точку М( 7.15. Найти эксцентриситет эллипса 5х2+8у2=40. 7.16. Составить каноническое уравнение гиперболы, проходящей через точку М( 7.17. Составить каноническое уравнение эллипса, который проходит через точки М1( 7.18. Найти координаты фокусов, эксцентриситет и уравнения асимптот гиперболы х2-4у2=1. Построить гиперболу и ее асимптоты. 7.19. Составить каноническое уравнение параболы, симметричной оси 0у и проходящей через точку М(-1,2). 7.20. Найти эксцентриситет эллипса х2+4у2=4.
Зачетное задание №2 Предел и непрерывность функции одной переменной. Производная. Исследование функции и построение графика.
Производной функции Обозначения: Таблица производных основных элементарных функций
Основные правила дифференцирования
Геометрический смысл производной.
Касательной к графику функции
Производная Справочный материал.
2. Задания для самостоятельной работы. Задание1. Дана функция Z= f (x, y). Найти частные производные 1 и 2 порядка.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.68.29 (0.008 с.) |





 | авс | = Vпар-да, построен-ного на векторах а, в, с.
| авс | = Vпар-да, построен-ного на векторах а, в, с.
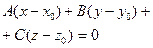
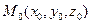 - точка на плоскости
- точка на плоскости
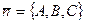 - нормальный вектор плоскости.
- нормальный вектор плоскости.
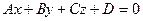
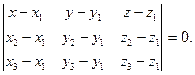
 ,
, 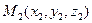 и
и
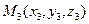 - заданные точки плоскости
- заданные точки плоскости


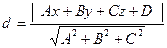


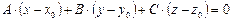

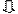
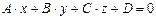
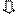
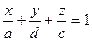
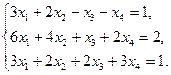
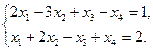
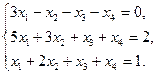
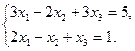
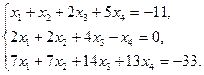
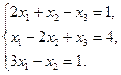
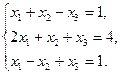

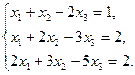
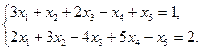
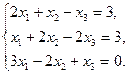
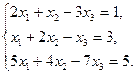

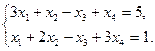
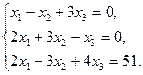
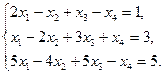
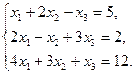
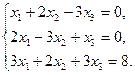
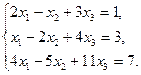

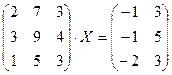
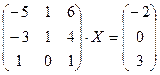


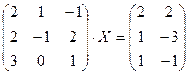
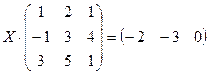

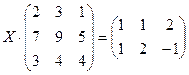
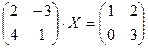
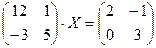
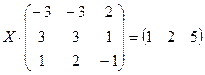
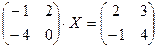

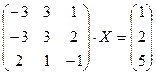
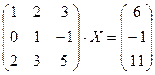


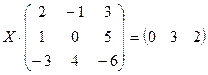
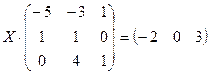
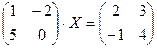
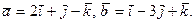
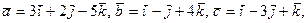 .
.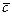 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям: 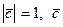 ортогонален векторам
ортогонален векторам 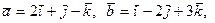 тройка векторов
тройка векторов  правая.
правая. , если он ортогонален векторам
, если он ортогонален векторам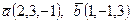 и
и 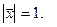
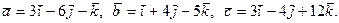 Найти проекцию вектора
Найти проекцию вектора  +
+  на направление вектора
на направление вектора 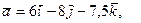 образует острый угол с осью 0Z. Найти координаты вектора
образует острый угол с осью 0Z. Найти координаты вектора 
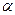 векторы
векторы  и
и 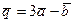 будут коллинеарны, если
будут коллинеарны, если  и
и 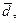 компланарный векторам
компланарный векторам 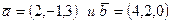 и ортогональный вектору
и ортогональный вектору 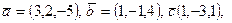 если за основание взят параллелограмм, построенный на векторах
если за основание взят параллелограмм, построенный на векторах 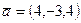 на направление вектора
на направление вектора  Найти проекцию вектора
Найти проекцию вектора  , если М1(0,-2), М2 (3,5).
, если М1(0,-2), М2 (3,5). , если М2 (4,5).
, если М2 (4,5).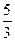 .
.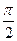 .
. ), если фокусы его находятся на оси 0х, а эксцентриситет
), если фокусы его находятся на оси 0х, а эксцентриситет  .
.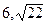 ), если ее действительная полуось равна 5.
), если ее действительная полуось равна 5.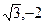 ) и М2 (
) и М2 (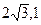 ). Найти его эксцентриситет.
). Найти его эксцентриситет.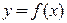 в фиксированной точке x называется предел при
в фиксированной точке x называется предел при 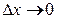 выражения
выражения 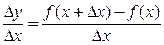 при условии, что этот предел существует.
при условии, что этот предел существует. .
.
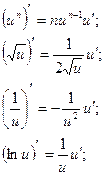
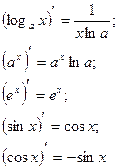
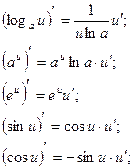


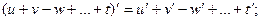

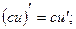 с - константа
с - константа


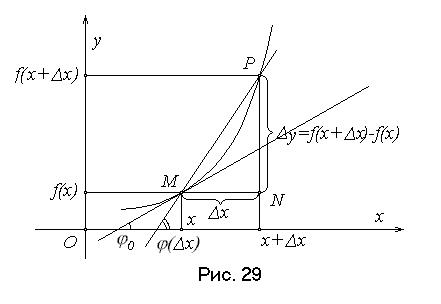
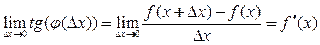 .
.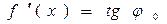 .
.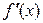 равна угловому коэффициенту касательной к графику функции
равна угловому коэффициенту касательной к графику функции 

 .
.
 ,
, 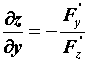 .
.

 где
где 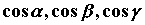 - направляющие косинусы вектора
- направляющие косинусы вектора  .
.