
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование иррациональных функцийСодержание книги
Поиск на нашем сайте
Интеграл
Пример:
Интеграл
Тригонометрические подстановки:
Интеграл
тогда
Интеграл
тогда
Интеграл
тогда
Интегралы от дифференциального бинома
Берется в трех случаях:
1).
2).
3)
2. Задания для самостоятельной работы Задание1. Вычислить неопределенный интеграл
Задание2. Вычислить определенный интеграл:
Задание 3. Решить задачу. 1. Найти площадь фигуры, ограниченной кривой 2. Найти площадь, ограниченную астроидой 3. Найти площадь, ограниченную одной аркой циклоиды 4. Найти площадь, ограниченную цепной линией 5. Найти площадь, ограниченную гиперболой 6. Найти площадь, ограниченную кубической параболой 7. Вычислить площадь фигуры, ограниченной параболами:
8. Вычислить площадь фигуры, ограниченной линиями: 9. Вычислить площадь фигуры, ограниченную дугами парабол 10. Вычислить площадь эллипса, заданного параметрическими уравнениями 11. Вычислить площадь, ограниченную гиперболой 12. Вычислить объем, образованный вращением вокруг оси 13. Найти объем тела, образованного вращением фигуры, ограниченной линиями: 14. Найти объем тела, ограниченного 15. Найти объем тела, образованного вращением фигуры, ограниченной линиями: 16. Найти объем тела, образованного вращением фигуры, ограниченной линиями: 17. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями 18. Вычислить длину дуги кривой 19. Найти длину дуги кривой 20. Вычислить длину дуги астроиды
Задание 4. Вычислить несобственные интегралы:
Задание 5. Применение определенного интеграла в экономических задачах. 1. Найти среднее значение издержек
2. Определить объем продукции, произведенной рабочим за второй час рабочего дня, если производительность труда характеризуется функцией
3. Определить запас товаров на складе, образуемый за два дня, если поступление товаров характеризуется функцией
4. Определить количество тракторов, выпущенных за пять лет, если годовой выпуск рос в арифметической прогрессии
5. Найти полные издержки производства, если объем продукции равен 42 единицам, а зависимость издержек от объема имеет вид
6. Дана функция предельных издержек
7. Под строительство гидроэлектростанции задан непрерывный денежный поток со скоростью
8. Пусть кривая предложения имеет вид 9. Чистые инвестиции
10. Найти объем продукции, произведенной за 4 года, если функция Кобба-Дугласа имеет вид
11. По данным исследований в распределении доходов в одной из стран кривая Лоренца может быть описана уравнением
12. Определить дисконтированный доход за три года при процентной ставке 8%, если первоначальные (базовые) капиталовложения составили 10 млрд.руб., и намечается ежегодно увеличивать капиталовложения на 1 млрд.руб.
13. Вычислить начальный вклад P, если выплаты должны составлять 100 в течение 4 лет, а процентная ставка равна 7.
14. Найти среднее значение издержек 15. Определить объем продукции, произведенной рабочим за четвертый час рабочего дня, если производительность труда характеризуется функцией
16. Найти полные издержки производства, если объем продукции равен 50 единицам, а зависимость издержек от объема имеет вид
17. Дана функция предельных издержек
18. Под строительство жилого дома задан непрерывный денежный поток со скоростью
19. Пусть кривая предложения имеет вид
20. Чистые инвестиции
21. Найти объем продукции, произведенной за 10 лет, если функция Кобба-Дугласа имеет вид
22. Определить дисконтированный доход за три года при процентной ставке 5%, если первоначальные (базовые) капиталовложения составили 6 млрд.руб., и намечается ежегодно увеличивать капиталовложения на 1 млн.руб.
23. Вычислить начальный вклад P, если выплаты должны составлять 50 в течение 8 лет, а процентная ставка равна 4.
Зачетное задание №5 Дифференциальные уравнения
Справочный материал
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.216.202 (0.008 с.) |

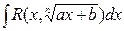 , берется подстановкой
, берется подстановкой  .
. .
. , берется подстановкой
, берется подстановкой  .
.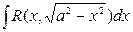 , берется подстановкой
, берется подстановкой  ,
, ,
,  ,
,  .
. , берется подстановкой
, берется подстановкой  ,
,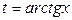 ,
, 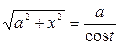 ,
, 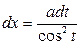 .
.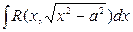 , берется подстановкой
, берется подстановкой 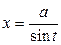 ,
, ,
, 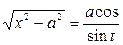 ,
, 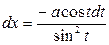 .
.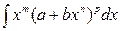 .
. - целое, решается разложением
- целое, решается разложением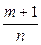 - целое, решается заменой
- целое, решается заменой 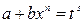 , где
, где  знаменатель дроби
знаменатель дроби 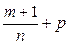 - целое, решается заменой
- целое, решается заменой 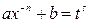 , где
, где 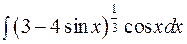



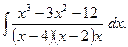

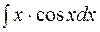
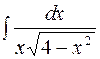
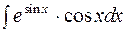
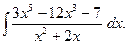


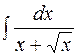
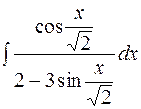
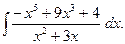



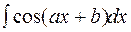



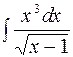
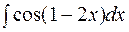
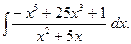
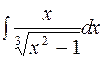
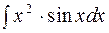
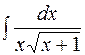
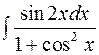
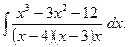
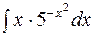
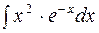

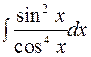
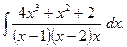
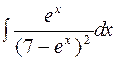


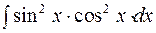
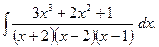
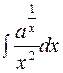
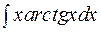
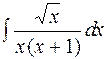



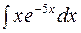

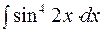

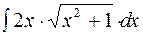
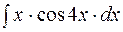

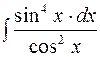

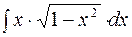
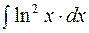
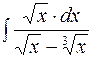

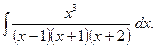


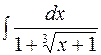
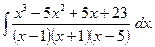

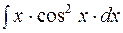
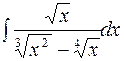
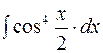

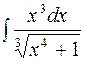


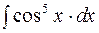
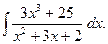
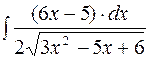

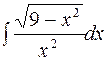

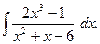





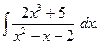





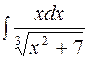
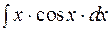



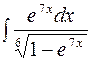
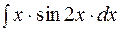


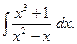
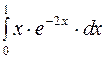

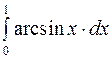
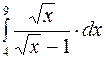
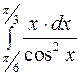
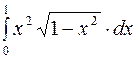
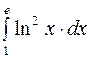
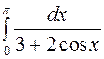
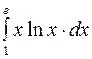
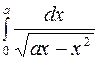
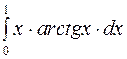
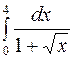
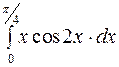
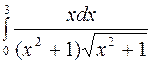



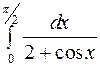


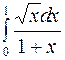
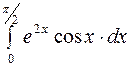
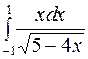


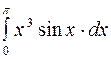
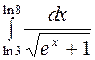
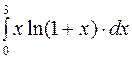
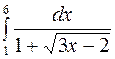
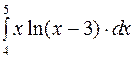
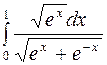


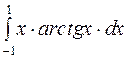
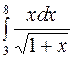
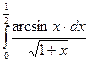

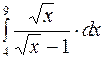
 и осью
и осью 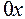 .
.
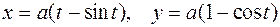 и осью
и осью  и прямыми
и прямыми 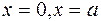 .
.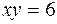 и прямой
и прямой 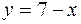 .
.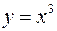 и прямыми
и прямыми 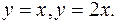
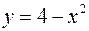 и
и 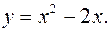
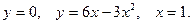
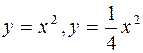 и прямой
и прямой 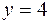 .
.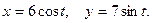
 и прямой
и прямой 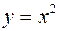 и
и 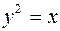 .
. (одной волной),
(одной волной), 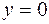 вокруг оси
вокруг оси  вокруг оси
вокруг оси  .
. вокруг оси
вокруг оси  вокруг оси
вокруг оси  вокруг оси
вокруг оси  между точками пересечения с осью
между точками пересечения с осью 
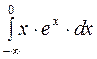
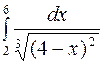
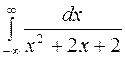
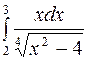
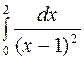
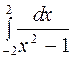

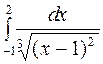

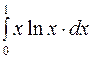
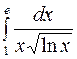
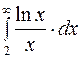
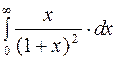
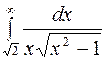
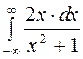
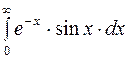
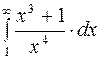
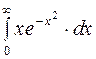
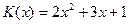 , выраженных в денежных единицах, если объем продукции x меняется от 0 до 4 единиц. Указать объем продукции, при котором издержки принимают среднее значение.
, выраженных в денежных единицах, если объем продукции x меняется от 0 до 4 единиц. Указать объем продукции, при котором издержки принимают среднее значение. .
.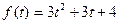 .
.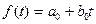 .
. .
. ,
, 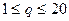 . Найти функцию издержек
. Найти функцию издержек  и вычислить издержки в случае производства 10 единиц товара, если известно, что издержки для производства первой единицы товара составили 50 рублей.
и вычислить издержки в случае производства 10 единиц товара, если известно, что издержки для производства первой единицы товара составили 50 рублей. (млрд руб\год) в течение 20 лет с годовой процентной ставкой p=5%. Найти дисконтированную стоимость этого потока.
(млрд руб\год) в течение 20 лет с годовой процентной ставкой p=5%. Найти дисконтированную стоимость этого потока.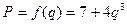 . Точка равновесия между спросом и предложением достигается при количестве товара q0=3. Определить добавочную выгоду производителя.
. Точка равновесия между спросом и предложением достигается при количестве товара q0=3. Определить добавочную выгоду производителя. . Определить приращение капитала за три года. Через сколько лет приращение составит 50000?
. Определить приращение капитала за три года. Через сколько лет приращение составит 50000? .
.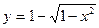 , где x – доля населения, y – доля доходов населения. Вычислить коэффициент Джини.
, где x – доля населения, y – доля доходов населения. Вычислить коэффициент Джини. , выраженных в денежных единицах, если объем продукции x меняется от 0 до 8 единиц. Указать объем продукции, при котором издержки принимают среднее значение.
, выраженных в денежных единицах, если объем продукции x меняется от 0 до 8 единиц. Указать объем продукции, при котором издержки принимают среднее значение. .
.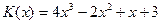 .
.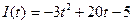 (млрд руб/год) в течение 3 лет с годовой процентной ставкой p=8%. Найти дисконтированную стоимость этого потока.
(млрд руб/год) в течение 3 лет с годовой процентной ставкой p=8%. Найти дисконтированную стоимость этого потока. . Точка равновесия между спросом и предложением достигается при количестве товара q0=5. Определить добавочную выгоду производителя.
. Точка равновесия между спросом и предложением достигается при количестве товара q0=5. Определить добавочную выгоду производителя.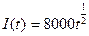 . Определить приращение капитала за шесть лет. Через сколько лет приращение составит 500000?
. Определить приращение капитала за шесть лет. Через сколько лет приращение составит 500000?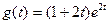 .
.


