
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратная матрица. Решение матричных уравнений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Матрица
где
где Внимание! Алгебраические дополнения вычисляются к элементам строки, а записываются в столбец. Если Обозначается обратная матрица
при этом ее определитель Для невырожденных матриц
Введение обратной матрицы позволяет решать матричные уравнения. В конечном счете, матричные уравнения сводятся к двум простейшим уравнениям:
Если матрица При поиске решения первое из уравнений надо умножать на обратную матрицу
►Пример 5. Найти решение матричного уравнения Решение. Решение в матричном виде определяется формулой (5), т.е. Для существования решения необходимо, чтобы матрица
Следовательно, матрица
Составим обратную матрицу
При вычислениях множитель ►Пример 6. Найти решение матричного уравнения Решение. Формулой (5) воспользоваться нельзя, так как матрица
Матрица
Проведем вычисления.
Определитель полученной матрицы
Итак, неизвестная матрица Упражнения. 1. Для заданных матриц найти обратную матрицу. а) Ответы: а) д) 2. Найти неизвестную матрицу из уравнений.
а)
г)
Ответы: а)
Ранг матрицы
Рангом матрицы К элементарным преобразованиям матрицы относятся: - транспонирование; - удаление или добавление строки (столбца), состоящей из нулей; - умножение строки (столбца) на число, отличное от нуля; - перестановка строк (столбцов); -прибавление к элементам какой-либо строки элементов другой строки, умноженных на постоянное число (тоже для столбцов). Выполняя элементарные преобразования над матрицей, получаем другую матрицу, называемую эквивалентной. Переход от исходной матрицы к эквивалентной обычно обозначается символом Используя перечисленные действия, матрицу можно преобразовать к треугольному виду, что позволяет легко определить ее ранг.
►Пример 7. Найти ранг матрицы Решение.
Минор При преобразовании матрицы мы проводили операции только со строками и по определенному алгоритму. Этот метод стандартный, но не является обязательным. С рангом матрицы связано понятие линейно зависимых (независимых) векторов. Пусть в пространстве
Линейной комбинацией векторов
где Если Векторы Векторы Если система из Ранг матрицы определяет наибольшее число линейно независимых строк (столбцов), рассматриваемых как векторы. Так в матрице
Матрица
Упражнения. 1. Найти ранг матриц: а) г) 2. Для матрицы примера 7 получить линейную комбинацию первых трех строк, равную пятой строке. Ответ:
Системы линейных уравнений. Основные понятия.
Системой
где Линейная система называется однородно й, если все свободные члены равны нулю.
В противном случае линейная система называется неоднородной. Решением системы (7) называется упорядоченная совокупность
при подстановке которых вместо Система, имеющая хотя бы одно решение, называется совместной, а система, не имеющая ни одного решения, - несовместной. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Однородная система (8) всегда совместна, так как она имеет очевидное решение: Две системы называются равносильными или эквивалентными, если любое решение одной из них является также решением и другой, и обратно, т.е. они имеют одно и то же множество решений. В частности, любые две несовместные системы являются эквивалентными. Линейную систему можно записать в матричной форме. Введем матрицы
Тогда систему (7) можно записать в виде матричного уравнения
а решение (9) в виде матрицы-столбца
Матрица коэффициентов
называется основной матрицей системы. Матрица, составленная из коэффициентов и свободных членов,
называется расширенной матрицей системы. Выражение «решить систему» означает: выяснить, совместна или несовместна система, а в случае совместности – найти все ее решения.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 925; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.007 с.) |

 называется обратной к квадратной матрице
называется обратной к квадратной матрице  , если
, если
 - единичная матрица, имеющая тот же порядок, что и матрица
- единичная матрица, имеющая тот же порядок, что и матрица  , и ее элементы находятся по формуле
, и ее элементы находятся по формуле ,
, - алгебраическое дополнение к элементу
- алгебраическое дополнение к элементу  .
. , то матрица
, то матрица  , т.е.
, т.е. ,
, .
. ,
, .
. или
или  .
. . (5)
. (5) . (6)
. (6) , если
, если  ;
;  .
. .
. .
.
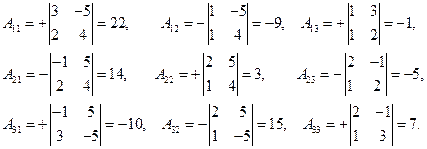
 ,
,  . ◄
. ◄ лучше оставлять перед матрицей и проводить умножение полученной матрицы на него на последнем этапе вычислений.
лучше оставлять перед матрицей и проводить умножение полученной матрицы на него на последнем этапе вычислений. , если
, если  .
. слева, получаем
слева, получаем .
. - квадратная и, если ее определитель не равен нулю, то решение заданного уравнения имеет вид
- квадратная и, если ее определитель не равен нулю, то решение заданного уравнения имеет вид ..
.. .
. . Следовательно, обратная матрица к матрице
. Следовательно, обратная матрица к матрице  существует, и можно найти матрицу
существует, и можно найти матрицу  ,
, ,
, .
. . ◄
. ◄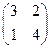 ; б)
; б)  ;в)
;в)  ;г)
;г)  ;д)
;д)  .
.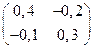 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; .
. ; б)
; б)  ;в)
;в)  ;
; ; д)
; д)  .
.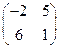 ; б)
; б)  ; д)
; д)  ) называется порядок отличного от нуля минора этой матрицы при условии, что все ее миноры высших порядков равны нулю. Минор наивысшего порядка, отличный от нуля, называется базисным минором или просто б азисом. Матрица может иметь несколько различных базисов. Для определения базиса над матрицей производят элементарные преобразования, при которых ранг матрицы не изменяется.
) называется порядок отличного от нуля минора этой матрицы при условии, что все ее миноры высших порядков равны нулю. Минор наивысшего порядка, отличный от нуля, называется базисным минором или просто б азисом. Матрица может иметь несколько различных базисов. Для определения базиса над матрицей производят элементарные преобразования, при которых ранг матрицы не изменяется. или
или  .
. .
.
 , а все миноры четвертого порядка равны нулю, т.к. содержат нулевую строку. Следовательно,
, а все миноры четвертого порядка равны нулю, т.к. содержат нулевую строку. Следовательно,  . ◄
. ◄ (множестве векторов с операциями сложения и умножения на число) имеется система из
(множестве векторов с операциями сложения и умножения на число) имеется система из  векторов
векторов
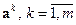 , называется выражение
, называется выражение ,
, - числа.
- числа. , то, комбинация
, то, комбинация  , называется тривиальной комбинацией. Она, очевидно, равна
, называется тривиальной комбинацией. Она, очевидно, равна  =(0,0,..,0), где
=(0,0,..,0), где  называются линейно независимыми, если любая нетривиальная комбинация этих векторов не равна нулевому вектору.
называются линейно независимыми, если любая нетривиальная комбинация этих векторов не равна нулевому вектору. называются линейно зависимыми, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору.
называются линейно зависимыми, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору. .
. .
. ; б)
; б)  ; в)
; в)  ;
; . Ответы: а) 4; б) 2; в) 4; г) 3.
. Ответы: а) 4; б) 2; в) 4; г) 3.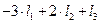 .
. неизвестными
неизвестными  (линейной системой) называется система вида
(линейной системой) называется система вида (7)
(7) - числа. Числа
- числа. Числа  называются коэффициентами системы, а числа
называются коэффициентами системы, а числа  - свободными членами.
- свободными членами. (8)
(8) , (9)
, (9) . Нулевое решение однородной системы называется тривиальным.
. Нулевое решение однородной системы называется тривиальным. – матрица коэффициентов при неизвестных,
– матрица коэффициентов при неизвестных, - матрица-столбец свободных членов,
- матрица-столбец свободных членов, - матрица-столбец неизвестных.
- матрица-столбец неизвестных. .
.




