
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы принятия решения (экспертные системы)Содержание книги
Поиск на нашем сайте
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ В ЗАДАЧАХ ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ Системы принятия решения (экспертные системы)
В настоящее время широкое распространение получили системы искусственного интеллекта (ИИ), имитирующие на компьютере мышление человека при решении различных задач. Система ИИ, созданная для решения задачи в конкретной области, называется экспертной системой (ЭС), или системой принятия решения. Факты и правила для системы принятия решения должны быть разработаны экспертом соответствующей предметной области.. Они хранятся в компьютере в специально организованной области памяти, называемой базой знаний (БЗ). Информация, которая предъявляется системе для анализа сочетания фактов в данный момент, хранится в компьютере в специально организованной области памяти, называемой базой данных (БД).
Пример разработки системы принятия решения Необходимо разработать систему принятия решения об аттестации знаний абитуриента на основе результатов тестирования. База знаний имеет вид табл. 1: Таблица 1
Правила вывода Если набранная сумма баллов меньше 280 - оценка "Неудовлетворительно". При сумме баллов в пределах 280-340 - оценка "Удовлетворительно". При сумме баллов 341 - 400 оценка "Хорошо". Если сумма больше 400 - "Отлично". 1. Общая схема решения Приведенная база знаний, разумеется, является лишь фрагментом базы знаний реальной системы аттестации абитуриента. Разработка системы принятия решений включает три основных этапа: · Создание базы данных для тестовой проверки разработанной системы принятия решения; · Формализация правил принятия решений на основе имеющихся правил вывода. Обычно схему решения записывают в виде специального графа – дерева решений;
· Компьютерная реализация системы. Система принятия решения может быть реализована с использованием языка программирования высокого уровня или в электронной таблице.
2. Разработка базы данных для системы принятия решения База данных табл. 2 создается на основе БЗ табл. 1, в которую добавляется столбец ответов. Очевидно, что для каждого абитуриента будет свой набор ответов и соответственно своя база данных. Если на заданный вопрос дается положительный ответ («Да»), то есть абитуриент продемонстрировал достаточные знания по этой теме, весовой фактор атрибута сохраняется. Если ответ отрицательный («Нет»), весовой фактор обнуляется. Таблица 2
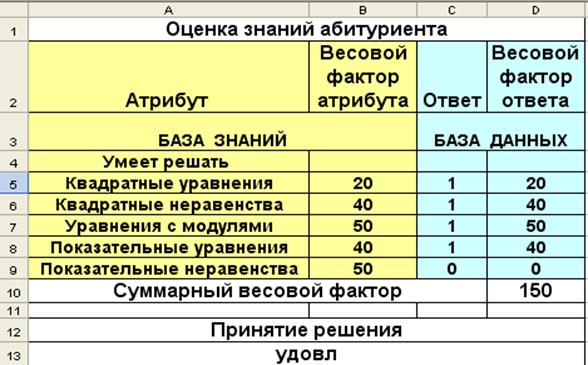
Просуммировав весовые факторы ответов в нашей базе данных, найдем суммарный весовой фактор S =310. Поскольку эта сумма баллов находится в диапазоне 280-340, согласно правилам вывода абитуриент должен получить оценку «Удовлетворительно». Заполнив базу данных ответами, следует те же самые ответы вводить в систему принятия решения, реализуемую в электронной таблице.
Дерево (граф) принятия решений строится на основе правил вывода. Граф принятия решений называется деревом, потому что имеет свои вершины и ветви. Вершины служат для проверки условий (обозначаются окружностями или эллипсами), а также для вывода сообщений о фактах и результатах решения (обозначаются прямоугольниками). Ветви соединяют вершины и указывают направления пути решения.
Рис. 7.1
4. Реализация системы принятия решений в электронной таблице Реализация системы принятия решений приведена в табл. 3 (режим показа формул) и в табл. 4 (режим показа вычислений). Таблица 3
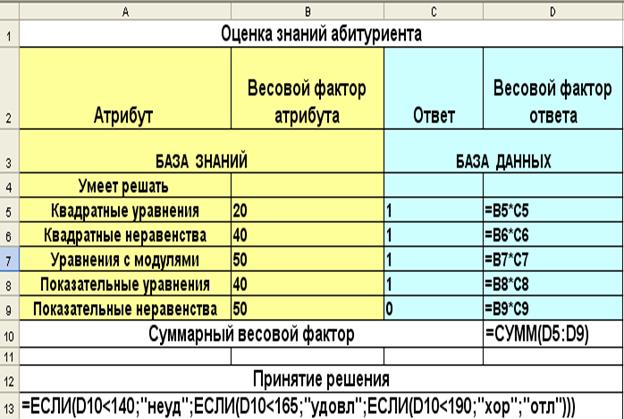
Таблица 4
6.2. Финансовые вычисления в электронных таблицах Решение Р =700 000 руб., r=20 %, n =4. S = P (1+0,2∙ n)=700000∙ (1+0,2∙1)=840 000 руб.
Задание 6.2. В банк на 1 год помещена сумма в $ 5000 под 10% годовых, простые проценты. Какая сумма будет на счету у вкладчика через год?
_________________________________________________________
Решение Введем в любую ячейку Excel формулу: =БС(20%;1;;700000). В результате в ячейке вычисляется значение –840000 р. Знак минус показывает, что эта сумма подлежит возврату. При работе с программой Calc формула имеет вид: =FV(20%;1;;700000). Примечание. Следует отметить, что функцию БС (FV) можно использовать для проведения операций по схеме простых процентов только в том случае, когда число периодов равно единице.
Решение Введем в любую ячейку Excel формулу: =БС(10%;1;;-5000). Обратите внимание! В качестве начального значения введено число 5000 со знаком минус, так как эта сумма отдана клиентом банку. Результатом будет значение 5500 р. со знаком плюс, поскольку эта сумма будет получена клиентом. При работе с программой Calc формула имеет вид: =FV(10%;1;;-5000).
Задание 6.3. Используя функции электронных таблиц, вычислить, какую сумму накопит клиент, поместивший в банк 35000 руб. под 15% годовых, простые проценты.
____________________________________________________________________
Сложные проценты
S= P(1+r)n. (6.4) Для вычисления по схеме сложных процентов в Excel используется функция БС, а в программе Calc - функция FV.
Решение Р=100 000 руб, r=20 %, n=3 года. S= P(1+r)n=100000(1+0,2)3=172 800 (руб).
_________________________________________________________
Решение Введем в любую ячейку Excel формулу: =БС(20%;3;;100000). При работе с программой Calc формула имеет вид: =FV(20%;3;;100000).
_________________________________________________________
Решение 1. Аналитические расчеты P=$10 000, r=12 %, n=2 года. Так как процентная ставка дана годовая, а период начисления процентов – квартал, сначала рассчитаем процентную ставку за период, она равна
Тогда число периодов (кварталов) равно 2Ÿ4=8. Накопленный долг равен S= P (1+ rn) n =10000(1+0,03)8=12 666,7 (долларов). 2. Решение в Excel. Вводим в любую ячейку формулу: =БС(12%/4;2*4;;-10000). Результат: 12666,7.
_________________________________________________________
____________________________________________________________________
____________________________________________________________________
6.2.4.
Теперь рассмотрим, как по будущему значению определить текущее (современное) значение. В этом случае в Excel используется финансовая функция ПС (приведенная сумма). В программе Calc, входящей в состав пакета программ OpenOffice.org, эта функция называется РV (Present Value). Функция имеет синтаксис =ПС(Ставка;Кпер;Плт;БС;Тип). Здесь БС – будущая сумма.
Пример 7. Вкладчик собирается положить деньги в банк на четыре года под 25 % годовых и накопить 15 000 руб. Какую сумму он должен вложить?
Решение S =15 000 руб., n =4, r =25 %. Из уравнения (6.4) найдем
_________________________________________________________
Решение Введем в любую ячейку Excel формулу: =ПС(25%;4;;15000). При работе с программой Calc формула имеет вид: =РV(25%;4;;15000). Результатом вычислений будет значение -6144 р.Знак минус показывает, что данную сумму клиент помещает в банк.
_________________________________________________________
Одна из серьезнейших задач, стоящих перед любым управляющим и экономистом – на основе анализа деятельности предприятия за прошлый период осуществить планирование его деятельности в следующем периоде. Рассмотрим задачу планирования производства на примере балансовой модели. Экономическая система состоит их трех отраслей. Объемы производства каждой из отраслей за предыдущий период, текущее производственное потребление в отраслях, а также прогнозируемый конечный спрос на продукцию каждой из трех отраслей приведены в табл. 5. Определить конечную продукцию каждой из отраслей за предыдущий период и план выпуска продукции в следующем периоде, считая, что технология производства не изменилась. Таблица 5
1. Математическая постановка задачи Для решения поставленной задачи можно использовать балансовую модель Леонтьева. Она представляет собой систему уравнений, каждое из которых выражает требование равенства (баланса) между количеством продукции, производимой отдельным экономическим объектом, и совокупной потребностью в этой продукции. В рассматриваемой задаче экономическая система состоит из трех отраслей. Обозначим: Хi - суммарный выпуск продукции отрасли i; xij - количество продукции отрасли i, необходимое для того, чтобы отрасль j произвела Xj единиц своей продукции; Yi - количество продукции отрасли i, оставшееся для внешнего потребления (конечная продукция). Тогда взаимосвязь отраслей в процессе производства и потребления отдельного продукта Хi (i =1, 2, 3) может быть описана в виде следующих уравнений:
Используем понятие технологических коэффициентов aij:
Тогда xij = aijXj и система уравнений (6.5) будет иметь следующий вид:
Или в матричной форме Х = АХ + Y, (6.7) где Х - вектор-столбец выпуска продукции в предыдущем периоде Y - вектор-столбец конечного спроса в предыдущем периоде Решим уравнение (6.7) относительно Х: Х-АХ=Y, отсюда, Х (Е-А) = Y, (6.8) где Е – единичная матрица. Из уравнения (7.8) получаем Х =(Е-А)-1 Y. (6.9) 2. Условие решения задачи (проверка продуктивности матрицы)
Для того чтобы система уравнений (6.7) имела единственное неотрицательное решение при любом векторе спроса Y, необходимо, чтобы матрица А была продуктивной. Экономический смысл продуктивности состоит в том, что существует такой план выпуска продукции, который каждая отрасль сможет реализовать при существующей технологии производства. Математически для продуктивности матрицы А необходимо и достаточно, чтобы сумма элементов каждого из столбцов матрицы А была положительна и строго меньше единицы. 3. Реализация балансовой модели в электронной таблице Компьютерная реализация балансовой модели в ЭТ показана в табл. 6 (режим показа формул) и в табл. 7 (режим вычислений). Таблица 6
Обратите внимание! 1. В программе Calc вместо функции МОБРиспользуется MINVERSE, а вместо функции МУМНОЖ - MMULT. 2. При работе с матричными операциями следует выделить диапазон ввода, набрать имя функции, ее аргументы и одновременно нажать три клавиши:Ctrl + Shift + Enter. Таблица 7
Пример 9. Рассчитать конечную продукцию отраслей для данных табл.5.
Y1 = 600 – 250 – 100 - 160 = 90 Y2 = 1000 – 150 – 500 – 0 = 350 Y3 = 800 – 0 – 300 – 400 = 100
____________________________________________________________________
____________________________________________________________________
Пример 10. Проверить продуктивность матрицы прямых затрат.
Решение
Матрица продуктивна, если суммы элементов ее столбцов положительны и строго меньше единицы. Суммы элементов каждого столбца заданной матрицы А соответственно равны:
Следовательно, матрица А продуктивна, отрасли могут справиться с выпуском продукции без изменения технологии.
Задание 6.10. Проверить продуктивность матрицы прямых затрат
______________________________________ ______________________________________ ______________________________________
На практике часто приходится искать наилучшее (оптимальное) решение, например дающее предприятию максимальную прибыль или обеспечивающее минимальные затраты. На компьютере подобные задачи можно решать, используя имеющуюся в табличных процессорах программу Поиск решения. Для работы с данной программой необходимо предварительно построить математическую модель задачи и определить ограничения решения. Транспортная задача Фирме необходимо организовать перевозку продукции с трех складов в пять магазинов. Сведения о наличии продукции на складах, о потребности в этой продукции у магазинов и о стоимости перевозки единицы продукции с каждого склада во все магазины приведены в табл. 8. Таблица.8
Считая, что можно везти продукцию с любого склада в любой магазин, следует так организовать перевозки, чтобы затраты были минимальными.
Решение задачи включает три этапа: 1. Построение математической модели. 2. Построение начального плана решения. 3. Оптимизация начального плана.
1. Построение математической модели а). Ввод обозначений. Обозначим: Хij – количество продукции, отправляемой со склада i в магазин j: Cij – стоимость перевозки единицы продукции со склада i в магазин j.
б). Определение ограничений. На переменные накладываются три ограничения: Первое. Исходя из физического смысла задачи, количество и стоимость продукции не может быть отрицательной величиной, то есть Хij ³ 0; Cij ³ 0. (6.10) Второе. Ограничения по предложению (со складов нельзя вывезти продукции больше, чем там имеется):
Третье. Ограничения по спросу (в магазины следует завезти не меньше продукции, чем им требуется):
в). Определение целевой функции Общая стоимость перевозок (целевая функция) равна
Необходимо определить такие неотрицательные значения переменных Х, которые удовлетворяют условиям (6.10), (6.11) и (6.12) и обращают в минимум целевую функцию Z (6.13). г). Проверка баланса. Необходимым и достаточным условием разрешимости транспортной задачи является условие баланса
где (при этом Si =
(при этом .
В нашем случае
следовательно, задача с балансом.
Задание 6.11. Определите суммарные затраты на перевозки, если с каждого склада в каждый магазин перевозится одна единица продукции.
______________________________________________________________________
______________________________________________________________________
__________________________________________________________________
__________________________________________________________________
2. Построение начального плана решения
Поскольку построение оптимального плана решения сразу невозможно, запланируем перевоз с каждого склада в каждый магазин одной единицы продукции. Начальный план решения, реализованный в электронной таблице, приведен в табл. 9 (режим показа формул) и в табл. 10 (режим показа вычислений).
Таблица 10
3. Оптимизация начального плана Используем режим Поиск решения.
Рис. 1
Рис. 2
2)Ввести данные: Установить целевую ячейку В17; Равной минимальному значению; Изменяя ячейки C11:G13. Для ввода ограничений щелкнуть по кнопке Добавить. Появится окно Добавление ограничений (рис.3). Ввести первое ограничение. Для этого заполнить поля:
Рис. 3
а ) Ссылка на ячейку: C11:G13; В среднем поле выбираем знак неравенства ³ Ограничение: 0, щелкнуть по кнопке Добавить. б) В появившемся новом окне Добавление ограничений: Ссылка на ячейку: C11:G13; В среднем поле выбираем цел, щелкнуть по кнопке Добавить. В программе Calc это ограничение не добавляется. На этом шаге его пропускаем. Аналогично п. а) ввести следующие ограничения. В11:В13 £ B5:В7; С15:G15 ³ C9:G9. После ввода каждого ограничения щелкнуть по кнопке Добавить, после ввода последнего – по кнопке ОК.
3 ) Для запуска режима Поиск решения щелкнуть по кнопке Выполнить (в программе Сalc – кнопка Решить).Появится окно Результаты поиска решения в Excel (а в программе OpenOffice.org Calc - окно Message Dialog). Щелкнуть по кнопке ОК. В результате улучшения плана получим оптимальный план (табл.11) стоимости перевозок с целевой функцией (стоимостью перевозок) Z =121.
Таблица 11
Рис. 3
БАЗЫ ДАННЫХ (БД) Основные понятия теории баз данных База данных - это поименованная совокупность структурированных сведений об объектах какой-либо предметной области Структурирование - это введение соглашений о способах представления данных. Неструктурированная запись информации о студентах: 1). Номер личного дела: 14693; Фамилия, Имя: Алексеев Максим; Дата рождения: 01.01.88; Специальность: 2201.
2). Шифр: 65788; Сергеева Ольга; д.р. 23 февраля 1987 г.; спец. 0604
Структурированная запись тех же данных
Система управления базами данных (СУБД) - это комплекс программных и языковых средств, необходимых для создания баз данных, поддержания их в актуальном состоянии и организации поиска в них необходимой информации. Наиболее популярны СУБД: FoxPro, Microsoft Access, OpenOffice.org Base.
Модели данных В СУБД происходит процесс логического представления данных, с которыми имеет дело пользователь, в язык ЭВМ и обратно. Общая логическая структура БД называется моделью данных. Различают три основные модели данных: иерархическую, сетевую и реляционную. Иерархическая модель данных Иерархическая структура представляет совокупность элементов, образующих граф (дерево) - рис. 5. К основным понятиям иерархической структуры относятся: уровень, элемент (узел), связь. Каждый узел (запись) описывает какой-то объект. К каждой записи есть только один путь от верхней (корневой) записи.
Первые системы управления базами данных использовали иерархическую модель данных (например, СУБД Фокус). Преимущество такой модели – ее наглядность (см., например, рис. 6). Недостатки – далеко не всякий объект можно представить в виде графа. Поэтому сегодня иерархические модели данных используются редко.
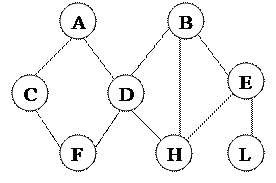
Рис. 6 Сетевая модель данных В сетевой структуре при тех же основных понятиях (уровень, узел, связь) каждый элемент может быть связан с любым другим элементом (рис. 7).
Рис. 7
Сетевые модели позволяют описывать любые предметные области (см. пример на рис. 8), однако такую подробную модель может быть трудно описать математически. Поэтому сегодня сетевые БД применяются, прежде всего, в банковских структурах (например, db Vista, AdaBas).
Фрагмент сетевой модели данных «Курсовые работы»
Рис. 8
Реляционная модель данных Реляционная модель использует организацию данных в виде двумерных таблиц. Примером реляционной БД может служить БД Студент (табл. 16). Реляционные СУБД – самые распространенные. Реляционные модели данных используют FoxPro, Microsoft Access, OpenOffice.org Base.
Создание базы данных Пример проектирования базы данных Пусть требуется создать базу данных для хранения сведений о результатах сдачи экзаменов каждым студентом одного факультета за весь период обучения. Назовем базу данных СТУДЕНТ.
1. Отбор атрибутов, сведения о которых должны храниться в БД В соответствии с заданием, в БД должны храниться следующие сведения о студентах: - номер зачетной книжки; - фамилия, имя, отчество; - дата рождения; - пол; - шифр специальности; - название специальности; - курс; - номер семестра; - название дисциплины; - название кафедры; - число учебных часов по дисциплине; - оценка; - дата сдачи экзамена.
2. Выбор системы управления базами данных (СУБД) В последнее время широкое распространение приобрели СУБД Access, входящая в состав Microsoft office и СУБД Base, входящая в пакет программ OpenOffice. org. Обе СУБД реализуют реляционную модель данных и алгоритм создания базы данных с использования обеих СУБД практически одинаков. Имеются небольшие, непринципиальные отличия в командах. (Подробнее о командах Access и Base см.в «Методических указаниях к выполнению лабораторных работ с СУБД»). Выбираем СУБД Access.
3. Проектирование схемы БД (разработка информационно-логической модели)
Согласно п. 1, в БД нужно хранить 15 атрибутов. Свести их в двумерную таблицу невозможно – будут повторяться записи об одном и том же студенте для разных курсов и дисциплин. Необходимо разбить атрибуты на несколько таблиц (рис. 10). Первая таблица БД Студент имеет ключ Номер и связывается со второй таблицей Ведомость по этому ключу. Тип связей этих таблиц 1:М или (1:¥), так как каждый студент сдает много экзаменов. Таблица Ведомость имеет два ключа (составной ключ). Ключ Номер используется для связи с таблицей Студент, а ключ Дисциплина – для связи с таблицей Учебный план. Таблица Учебный пла н имеет ключ Дисциплина. Тип связей таблицы Ведомость и Учебный план 1:1. Такое распределение всех атрибутов БД по трем таблицам обеспечивает отсутствие повторяющихся записей о каждом студенте, а наличие связей этих таблиц по ключам обеспечивает возможность обращения сразу ко всем таблицам. 4. Создание схем таблиц БД для машинных носителей (разработка логической структуры БД) Первый этап создания базы данных в СУБД Access или Base заключается в описании структуры каждой таблицы. Следует указать имена всех полей, тип хранящейся в них информации, размер поля. Для дробных чисел нужно также установить точность (количество знаков после запятой), для данных типа Дата/Время – формат (например, краткий – 20.10.08, полный – 20 октября 2008 г.).
Опишем схему (структуру) таблиц СТУДЕНТ (табл. 17), ВЕДОМОСТЬ (табл. 18) и УЧЕБНЫЙ ПЛАН (табл. 19).
Рис. 10
СТУДЕНТ Таблица 17
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 353; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.182.126 (0.022 с.) |

 6.1.1. Основные понятия теории систем принятия решений
6.1.1. Основные понятия теории систем принятия решений
 Задание 6.1. Определите оценку абитуриента для следующей базы данных
Задание 6.1. Определите оценку абитуриента для следующей базы данных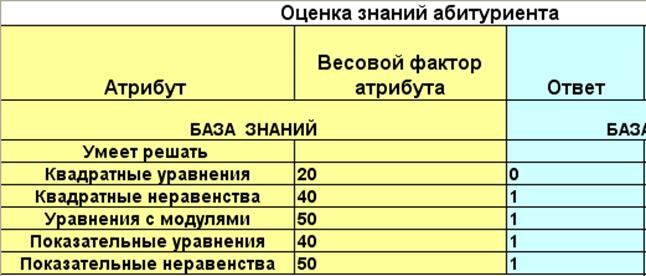




 Пример 3. Используя функции электронных таблиц, вычислить накопленную сумму в задании 6.2.
Пример 3. Используя функции электронных таблиц, вычислить накопленную сумму в задании 6.2.
 .
. (руб).
(руб). (6.5)
(6.5)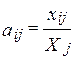 - количество продукции отрасли i, необходимое для того, чтобы отрасль j произвела одну единицу своей продукции.
- количество продукции отрасли i, необходимое для того, чтобы отрасль j произвела одну единицу своей продукции. (6.6)
(6.6) - матрица прямых затрат;
- матрица прямых затрат;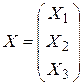 ;
; .
.

 ______________________________________
______________________________________ (6.11)
(6.11)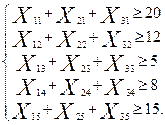 (6.12)
(6.12) (6.13)
(6.13) , (6.14)
, (6.14) - суммарное количество продукции на складах
- суммарное количество продукции на складах - количество продукции на одном складе, i =1, 2, 3);
- количество продукции на одном складе, i =1, 2, 3); - суммарное количество продукции, требуемое в магазинах
- суммарное количество продукции, требуемое в магазинах - количество продукции, которое требуется j- му магазину, j =1, 2, …,5)
- количество продукции, которое требуется j- му магазину, j =1, 2, …,5) ;
; =60,
=60, Таблица 9
Таблица 9
 1) После выполнения команд Сервис, Поиск решения открывается диалоговое окно Поиск решения (для Excel оно представлено на рис.1, а для Calc на рис.2).
1) После выполнения команд Сервис, Поиск решения открывается диалоговое окно Поиск решения (для Excel оно представлено на рис.1, а для Calc на рис.2).



 Таблица 16
Таблица 16




 1
1
 Дисциплина
Дисциплина



