
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Образец решения типовых задач.
1. Вычислить определитель: а) непосредственным разложением по б) непосредственным разложением по Решение. а) вычисляем определитель разложением по элементам первой строки:
Тогда б) вычисляем определитель непосредственным разложением по элементам второго столбца:
Тогда Ответ: 2. а) Найти матрицу
Решение: 1) Транспонируем матрицу 2) Вычисляем произведение матриц
3) Находим матрицу
4) Находим матрицу
Ответ: б) Найти собственные числа и векторы матрицы Множество собственных чисел матрицы совпадает с множеством корней характеристического уравнения матрицы Решение: 1) Составляем характеристическое уравнение матрицы
Записываем его в виде алгебраического уравнения и находим действительные корни (среди них могут быть и кратные):
Таким образом, собственными числами матрицы 2) Находим собственные векторы матрицы 2.1) Составляем матричное уравнениедля нахождения собственных векторов или
записываем его в виде системы линейных уравнений:
2.2) Составляем матричное уравнениедля нахождения собственных векторов или
записываем его в виде системы линейных уравнений: Ответ:
3. Дана система уравнений: а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса. Решение. А) Метод Крамера. 1а) Вычисляем определитель системы и проверяем, что он отличен от нуля:
2а) Так как 3а) Вычисляем определители
4а) Находим решение: 5а) Выполняем проверку: Ответ: Б) Метод обратной матрицы. 1б) Записываем систему уравнений в матричном виде:
2б) Вычисляем определитель системы и проверяем, что он отличен от нуля:
3б) Так как
4б) Находим обратную матрицу
Тогда 5б) Находим решение:
6б) Выполняем проверку: Ответ: В) Метод Гаусса. 1в) Записываем расширенную матрицу системы:
2в) Выполняем прямой ход метода Гаусса. В результате прямого хода матрица системы
Замечание. Если при выполнение преобразования расширенной матрицы 3в) Выполняем обратный ход метода Гаусса. Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: 4в) Выполняем проверку: Ответ:
4. Найти общее решение для каждой из данных систем методом Гаусса: а) Решение. 1а) Записываем расширенную матрицу системы:
2а) Выполняем прямой ход метода Гаусса.
Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных 3а) Выполняем обратный ход метода Гаусса. Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: Тогда общее решение системы запишется в виде: 4а) Выполняем проверку:
Ответ: б) Решение. 1а) Записываем расширенную матрицу системы:
2а) Выполняем прямой ход метода Гаусса.
Замечание. В результате прямого хода матрица системы Если, при выполнении преобразования расширенной матрицы Для выполнения условия
Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы, с учётом перестановки местами столбцов, образуют первый и второй столбцы коэффициентов при неизвестных
3б) Выполняем обратный ход метода Гаусса. Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: Тогда общее решение системы запишется в виде:
4б) Выполняем проверку:
Ответ: в) Решение. 1в) Записываем расширенную матрицу системы:
2в) Выполняем прямой ход метода Гаусса.
При выполнении преобразования расширенной матрицы Ответ: Система несовместна. 5. Исследовать квадратичную форму на знакоопределённость (по критерию Сильвестра). а) Решение. 1а) Записываем матрицу квадратичной формы: 2а) Проверяем является ли матрица 3а) Вычисляем угловые миноры матрицы Ответ: Квадратичная форма положительно определена. 1б) Записываем матрицу квадратичной формы: 2б) Вычисляем её определитель 3б) Вычисляем угловые миноры матрицы Ответ: Квадратичная форма знакопеременна.
6. Даны векторы
Решение. 1a). Находимвектор
= 2а) Находимвектор
= 3а) Вычисляем скалярное произведениевекторов
б) Вычисляем векторное произведение векторов
= 1в) Покажем, что векторы
Так как 2в) Записываем разложение вектора
Коэффициенты разложения 3в) Записываем векторное уравнение относительно
Таким образом: Ответ: 7. Даны вершины треугольника а) длину стороны в) уравнение медианы г) уравнение высоты д) длину Решение. Сделаем чертёж:
а) Длинустороны
б) Уравнение стороны
в) Уравнение медианы
Тогда:
г) Уравнение высоты д) Длину
е) Площадь треугольника Ответ: а) г)
|
||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.97.189 (0.161 с.) |


 строке;
строке; столбцу;
столбцу;
 .
.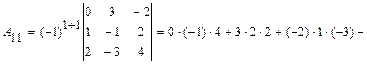





 =
=  =
= 

 .
.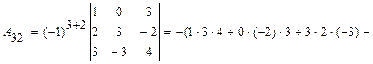



 .
. .
.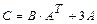 , если:
, если: ,
,  .
. :
:  .
. :
:

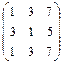 .
. :
:
 .
. :
: 

 .
. .
.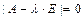 , а множество собственных векторов, отвечающих собственному числу
, а множество собственных векторов, отвечающих собственному числу  , совпадает с множеством ненулевых решений матричного уравнения:
, совпадает с множеством ненулевых решений матричного уравнения:  , определяемым методом Гаусса.
, определяемым методом Гаусса. .
.



 ,
,  .
. и
и  и
и  .
. , отвечающих собственному числу
, отвечающих собственному числу 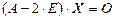

 ,
, и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе
и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе  , имеющей специальный (трапециевидный) вид. Такая система имеет бесконечно много решений, которые записывают в виде общего решения. Для записи общего решения этой системы указываем её базисные и свободные неизвестные. Базисными являются неизвестные, столбцы коэффициентов системы при которых образуют базисный минор матрицы этой системы. Такой минор образует, например, столбец коэффициентов при неизвестной
, имеющей специальный (трапециевидный) вид. Такая система имеет бесконечно много решений, которые записывают в виде общего решения. Для записи общего решения этой системы указываем её базисные и свободные неизвестные. Базисными являются неизвестные, столбцы коэффициентов системы при которых образуют базисный минор матрицы этой системы. Такой минор образует, например, столбец коэффициентов при неизвестной  :
:  . Поэтому выбираем в качестве базисной – неизвестную
. Поэтому выбираем в качестве базисной – неизвестную  и
и  . Свободным неизвестным придаём разные, произвольные постоянные значения:
. Свободным неизвестным придаём разные, произвольные постоянные значения:  ,
,  , где
, где  ,
, 
 , одновременно, и выражаем через них значение базисной неизвестной из уравнения системы:
, одновременно, и выражаем через них значение базисной неизвестной из уравнения системы:  . Тогда общее решение системы, задающее множество всех собственных векторов
. Тогда общее решение системы, задающее множество всех собственных векторов  .
. , отвечающих собственному числу
, отвечающих собственному числу 

 ,
, и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе
и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе  , имеющей специальный (трапециевидный) вид. Система имеет бесконечно много решений. Для записи её общего решения указываем базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных
, имеющей специальный (трапециевидный) вид. Система имеет бесконечно много решений. Для записи её общего решения указываем базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных  . Поэтому выбираем в качестве базисных – неизвестные
. Поэтому выбираем в качестве базисных – неизвестные  , где
, где  и выражаем через неё значения базисных неизвестных
и выражаем через неё значения базисных неизвестных  . Тогда общее решение системы, задающее множество всех собственных векторов
. Тогда общее решение системы, задающее множество всех собственных векторов  , отвечающих собственному числу
, отвечающих собственному числу  ,
,  . Требуется:
. Требуется:
 .
. , то система имеет единственное решение, определяемое формулами Крамера:
, то система имеет единственное решение, определяемое формулами Крамера: 
 :
:
 ,
,
 ,
,
 .
. .
.
 .
. .
. или
или 

 , то матрица системы
, то матрица системы  и единственное решение системы определяется формулой:
и единственное решение системы определяется формулой: или
или 
 (методом присоединённой матрицы):
(методом присоединённой матрицы): .
.


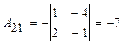

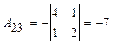


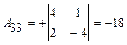
 .
.
 .
. .
.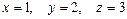 .
. .
. должна быть преобразована с помощью элементарных преобразований строк к матрице
должна быть преобразована с помощью элементарных преобразований строк к матрице  треугольного или трапециевидного вида с элементами
треугольного или трапециевидного вида с элементами 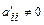 . Система уравнений, матрица которой
. Система уравнений, матрица которой  , имеет единственное решение, а система уравнений, матрица которой
, имеет единственное решение, а система уравнений, матрица которой  , имеет бесконечно много решений.
, имеет бесконечно много решений.




 . В результате элементарных преобразований матрица
. В результате элементарных преобразований матрица  . Система уравнений, матрица которой
. Система уравнений, матрица которой  в преобразованной матрице
в преобразованной матрице  появляется строка
появляется строка  , где
, где  , то это говорит о несовместности исходной системы уравнений.
, то это говорит о несовместности исходной системы уравнений. и последовательно из уравнений системы, начиная с последнего, находим значения всех неизвестных:
и последовательно из уравнений системы, начиная с последнего, находим значения всех неизвестных: 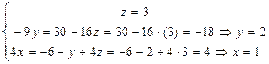 .
.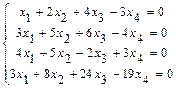 .
. .
.

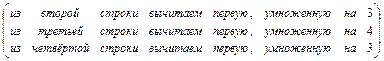




 .
. . Поэтому выбираем в качестве базисных – неизвестные
. Поэтому выбираем в качестве базисных – неизвестные  .
. . Свободным неизвестным придаём разные, произвольные постоянные значения:
. Свободным неизвестным придаём разные, произвольные постоянные значения:  ,
,  , и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных:
, и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных:  .
. .
.
 .
. .
. .
.






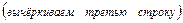
 .
. . Поэтому выбираем в качестве базисных – неизвестные
. Поэтому выбираем в качестве базисных – неизвестные  . Свободным неизвестным придаём разные, произвольные постоянные значения:
. Свободным неизвестным придаём разные, произвольные постоянные значения:  ,
,  .
.
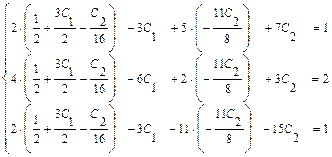

 .
. .
.



 .
. , соответствующая уравнению
, соответствующая уравнению 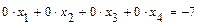 , которому не удовлетворяет ни один набор значений неизвестных
, которому не удовлетворяет ни один набор значений неизвестных  , что говорит о несовместности исходной системы уравнений.
, что говорит о несовместности исходной системы уравнений. ; б)
; б) 
 .
. и проверяем, равен ли он нулю:
и проверяем, равен ли он нулю:  . Так как
. Так как  , то матрица
, то матрица 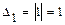 ,
,  ,
,  . Так как выполняется условие:
. Так как выполняется условие:  ,
,  ,
,  , то по критерию Сильвестра квадратичная форма положительно определена.
, то по критерию Сильвестра квадратичная форма положительно определена. .
. . Так как
. Так как 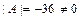 , то матрица
, то матрица  ,
,  . Так как два угловых минора нечётного порядка имеют разные знаки:
. Так как два угловых минора нечётного порядка имеют разные знаки: 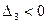 , то по критерию Сильвестра квадратичная форма знакопеременна.
, то по критерию Сильвестра квадратичная форма знакопеременна. :
:  ;
;  ;
;  ;
;  . Требуется: а) вычислить скалярное произведение векторов
. Требуется: а) вычислить скалярное произведение векторов  , если
, если  ,
,  ; б) вычислить векторное произведение векторов
; б) вычислить векторное произведение векторов 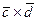 ; в) показать, что векторы
; в) показать, что векторы  образуют базис
образуют базис  и найти координаты вектора
и найти координаты вектора  в этом базисе.
в этом базисе.

 .
.

 .
.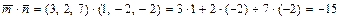 .
.

 образуют базис
образуют базис  .
. , то векторы
, то векторы  единственным образом можно разложить по векторам этого базиса.
единственным образом можно разложить по векторам этого базиса. :
: или
или  .
. ,
,  ,
,  называют координатами вектора
называют координатами вектора  и записывают:
и записывают: 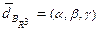 .
. , и находим единственное решение системы, например, по формулам Крамера:
, и находим единственное решение системы, например, по формулам Крамера: , где
, где ,
,  ,
,  ,
, 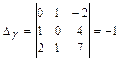 .
. ,
,  ,
, 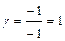 . Следовательно, разложение имеет вид:
. Следовательно, разложение имеет вид:  или кратко:
или кратко:  .
. .
. :
:  ,
,  ,
,  Требуется найти:
Требуется найти: ; б) уравнение стороны
; б) уравнение стороны 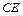 , проведённой из вершины
, проведённой из вершины  , проведённой из вершины
, проведённой из вершины  ;
; высоты
высоты  треугольника
треугольника  . Сделать чертёж.
. Сделать чертёж.
 :
: ,
, .
. и
и  , и записываем его в виде общего уравнения прямой:
, и записываем его в виде общего уравнения прямой:

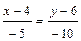

 .
. , и записываем его в виде общего уравнения прямой. Неизвестные координаты точки
, и записываем его в виде общего уравнения прямой. Неизвестные координаты точки  находим как координаты точки, делящей сторону
находим как координаты точки, делящей сторону  пополам:
пополам: ;
;  .
.


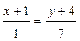

 .
.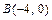 перпендикулярно вектору
перпендикулярно вектору 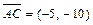 , который принимаем за нормальный вектор прямой
, который принимаем за нормальный вектор прямой 

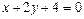
 высоты
высоты  :
: .
. . Откуда
. Откуда  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  .
.


