
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратная матрица: определение, свойства, ур-е существования.Содержание книги
Поиск на нашем сайте
Пусть задана кв. матрица А.Если сущ-т матрица В, такая что А*В=Е,то гов что матрица В явл обратной по отношению к мат А: В=А-1, А*А-1=Е. Свойства: 1)Обратная и исходная матрицы перестановочны и матрица,обратная обратной, совпадает с исходной: А*А-1=А-1*А=Е. 2)Единственность матрицы:если для данной матрицы обратная мат сущ-т,то она только одна. Как выяснить явл ли кв. матрица обратной? Пусть исход матрица А имеет вид: а11 а12 а13 А= а21 а22 а23 а31 а32 а33 Предпол что имеется какая-то мат В, В=(хij)=А-1,кот явл обратной по отношению к исходной мат-це А. Тогда должно выполняться: а11 а12.. а1n x11 x12.. x1n 10….0 а21 а22.. а2n * x21 x22.. x2n = 010...0 …………… ………….. ……. а31 а32.. а3n xm1 xm2.. xmn 000001 Это матричное ур-е можно переписать в виде системы n2 линейных ур-й с n2 неизвестными. 9.Обращение матрицы методом Жордана. Как известно, метод Жордана не требует предварительного исследования системы уравнений на совместность — ее исследование и решение проводятся одновременно. Достоинством явл и то что все коэф-ты в соотв-х СЛАУ явл одинаковыми. Выпишем матрицу А и припишем к ней столбцы свободных членов всех n подсистем:
Как обычно, будем подвергать элементарным преобразованиям систему строк этой вспомогательной матрицы. Приписанные столбцы свободных членов подсистем уравнений образуют единичную матрицу того же порядка, что и данная матрица А. В случае совместности системы уравнений на некотором этапе преобразований на месте матрицы А получится единичная матрица, и тогда каждый столбец приписанной матрицы будет представлять решение соотв-щей подсистемы ур-й, т.е. на месте этой матрицы появится обратная матрица. Схема обращения невырожденной матрицы А кратко может быть записана в виде (А,Е)->(Е,А-1).Если на некотором этапе процесса преобразований вспомогательной матрицы (1.2.39) в матрице А появится строка нулей, то это будет свидетельствовать о вырожденности матрицы А и, следовательно, о ее необратимости. 10 Обращенный базис СЛАУ. Приведение СЛАУ к предпочитаемому виду с помощью обращенного базиса. Дана система т линейных алгебраических уравнений с п неизвестными (т < п):
Исследуем ее, вычислив ранги матрицы СЛАУ и расширенной матрицы с помощью миноров. Предположим, что система оказалась совместной, все уравнения линейно зависимы, и пусть, для определенности, ненулевой минор Мт наивысшего порядка m (базисный минор) порождается подматрицей В, составленной из коэффициентов при первых т неизвестных. Матрицу В назовем базисной. Найдем для нее обратную матрицу B-1:
a11….а1m u11….u1m А= ………,B-1= ………, Mm=|B| am1….amm um1….umm Матрицу В-1 часто называют обращенным базисом. В матричной форме система алгебраических ур-й (1.2.43) записывается следующим образом:
где (слева проставлены в скобках размеры соотв-х матриц): (т х п) А — матрица коэффициентов; (n х 1) х — вектор-столбец неизвестных; (mх1) b — вектор-столбец правых частей ур-й. Разобьем вектор х на вектор базисных переменных хB (первые т переменных) и вектор свободных переменных xR (остальные п-т перем-х).Тогда матрица A соотв-щим образом разделится на подматрицы В (коэффициенты при базисных переменных) и R (коэффициенты при свободных переменных). При таком разделении матричное уравнение (1.2.45) примет вид BxB+RxR=b. (1.2.46) Поскольку базисная матрица В невырожденна,то обратная матрица В-1 существует. Умножим соотношение (1.2.46) слева на В-1, тогда с учетом того, что B-1B = Е, получим Матричное соотношение (1.2.47) в развернутой алгебраической форме записывают след образом: х1+q1,m+1*xm+1+…+q1n*хn=h1 х2+q2,m+1*xm+1+…+q2n*хn=h2 . .............. хm+qm,m+1*xm+1+…+qmn*хn=hm Мы пришли к предпочитаемому эквиваленту исходной СЛАУ. Базисными оказались те первые т неизвестных, из коэффициентов при которых был составлен ненулевой минор наивысшего порядка при исследовании системы.Т.о., матрица G системы (1.2.48) и матрица А системы (1.2.1), а также матрицы-столбцы h и b их правых частей связаны соотношениями: G=B-1A, h=B-1b 11. Задача оптимального производственного планирования и ее математическая модель.
Известны прибыль, полученная предприятием от производства и реализации продукции jго вида. Требуется составить план производства продукции: x = (x1, x2, x3,...xn), при котором предприятие получит наибольшую прибыль. Суммарная
прибыль предприятия
а21x1 + a22x2 + … a2nxn ≤ b2 ..... аm1x1 + am2x2 + … amnxn ≤ bm.
где bi-запас ресурса iго вида, x1≥0, x2≥0,...xn≥0. Математическая постановка задачи: Найти неотрицательные значения переменных xj, j=1,n, при которых линейная форма z =
aijxj ≤ bi xj≥ 0; i=
12. Общая задача математического прог-раммирования. Задачу линейного программирования нередко формулируют как задачу минимизации или макси-мизации линейной формы L=c1x1+c2x2+...cnxn (1) при ограничениях x1≥0, x2≥0,...xn≥0 и ∑ aijxj≤bi, i=1,2,...m1, ∑ aijxj=bi, i= m1+1, m1+2,...m2, ∑ aijxj≥bi, i= m2+1, m2+2,...m. Такую запись называют общей задачей линейного программирования. Обозначим через А матрицу системы линейных уравнений:
а11x1 + a12x2 + … a1nxn = b1 а21x1 + a22x2 + … a2nxn = b2 (2) ..... аm1x1 + am2x2 + … amnxn = bm.
Через X и B – матрицы-столбцы (векторы) неизвестных и свободных членов:
А =......, X=..., B=... am1... amn xn bm а также введем в рассмотрение n-мерный вектор C = (с1 … сn), компонентами которого служат коэффициенты линейной формы (1), и n-мерный нуль-вектор 0 (0, 0, …, 0). Тогда линейную форму (1) можно рассматривать как скалярное произведение L=CX (3), систему линейных уравнений (2) заменить одним матричным уравнением AX=B (4), а условия x1≥0, x2≥0,...xn≥0 записать в виде X≥ 0 (5). Поэтому часто основную задачу линей-ного программирования кратко записывают как задачу минимизации линейной формы (3) при линейных ограничениях (4) и (5). 13. Различные формулировки задачи линей-ного программирования, функция цели, до-пустимые и оптимальные решения. Основная задача ЛП, ее векторная и матричная формы записи. Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задчи, в которых необходимо решить с-му линейных алгебраических уравнений или неравенств и среди всех неотрицательных решений найти то решение, при котором линейная однородная функция принимает наибольшее или наименьшее значение. Изучение методов исследования и решения математических задач указанного типа составляет содержание раздела математики, кот. Принято называть линейным программированием.
а11x1 + a12x2 + … a1nxn = b1 а21x1 + a22x2 + … a2nxn = b2 (1) ..... аm1x1 + am2x2 + … amnxn = bm. Где неизвестные могут принимать только неотрицательные значения x1≥0, x2≥0,...xn≥0 (2), и линейная однородная ф-я от тех же переменных L=c1x1+c2x2+...cnxn (3). Требуется среди всех решений системы уравнений (1) найти такое неотрицательное решение, при котором линейная форма (3) принимает наименьшее возможное значение. Любое неотрицательное значение системы называют допустимым, а допустимое решение, при котором целевая ф-я (3) принимает наименьшее значение – оптимальным решением задачи ЛП (1)-(3). Если в матем-й модели какой-либо задачи планирования будут содержаться линейные неравенства, то их можно заменить линей-ными уравнениями с помощью дополнитель-ных неотрицательных неизвестных.
aijxj ≤ bi xj≥ 0; i=
Для приведения линейной задачи произ-водственного планирования к основной за-даче линейного программирования необходи-мо: 1. Ф-я z заменяется на “-z”. 2. В левой части сис-мы ограничений СЛАН вводится по одной искусствен-ной переменной в каждое из неравен-ств. Найти план производства xj, j=
aijxj + x’i = bi xj ≥ 0; x’i≥0, i= Исходные параметры задачи могут быть представлены в виде технологической матрицы A затрат ресурсов на единицу продукции каждого вида, вектора B объемов ресурсов и вектора C удельной прибыли: Матричная форма записи:
14. Геометрическая интерпретация задачи ЛП и симплексного метода. Графическое решение задачи ЛП с 2мя переменными.
15. Симплексметод ЛП: задача ЛП в предпочитаемой форме, выражение функции цели через свободные неизвестные, вычис-ление относительных оценочных коеффици-ентов ∆j и значение целевой функции соответ-ствующих данному базисному допустимому решению. Рассмотрим частный случай общей задачи, когда система уравнений имеет предпочитаемый вид, при этом правые части всех уравнений неотрицательны.
x1 + g1,m+1xm+1 +... + g1nxn = h1, x2 + g2,m+1 xm+1 +... + g2nxn = h2, (2) ............ xm + gm,m+1 xm+1 +... + gmnxn = hm
и xj≥0, j = 1,2,...n (3). Одним из допустимых решений задачи линейного программирования (1)-(3) будет базисное неотрицательное решение системы (2): x1=h1, x2=h2,...xm=hm, xm+1=0,...xn=0 (4), ему соответствует значение целевой ф-ии равное L0=c1h1+c2h2+...cmhm+cm+1*0+...+cn*0 = Надо исследовать, является ли решение (4) оптимальным (т.е. является ли значение (5) наименьшим из всех возможных значений целевой ф-ии (1), отвечающих различным неотрицательным решениям системы (2)). Учитывая что система уравнений (2) имеет предпочитаемый вид, находим для нее общее решение: xi=hi-gi,m+1xm+1-...-ginxn, i=1,2,...,m (6). Если свободным неизвестным придавать какие-нибудь неотрицательные значения, то будем получать различные решения системы (2), среди которых нас интересуют только неотрицательные. Подставляя их компоненты в линейную форму (1), можно подсчитать соответствующие значения целевой функции. Если переписать выражение (1) в виде:
- L = c1x1+c2x2+...cmxm+ cm+1xm+1+...+cnxn=0 (7). Для того чтобы исключить базисные неизвестные из (7), достаточно умножить первое уравнение системы (2) на c1, второе- на c2, …, m-e на cm, сложить полученные произведения и из результата вычесть уравнение (7). Получим L=∆m+1xm+1+...+∆nxn=L0 (8), где ∆j = c1g1j + c2g2j +... + cmgmj - cj, j=1,2,...n (9) или ∆j = zj - cj, zj= ∆j = CGj- cj, j=1,2,...n. А L0 = CH. Для проведения указанных вычислений обычно составляют таблицу (ТАБЛИЦА 1) Ее называют – первой симплекс таблицей. Из Ур-я (8) получаем выражение целевой ф-ии L через свободные неизвестные: L=L0-∆m+1xm+1-...-∆nxn.
16. Симплексный метод ЛП: исследование данного базисного допустимого решения на оптимальность, условия оптимальности в случае минимизируемой и максимизируемой функции цели. Из выражения L=L0-∆m+1xm+1-...-∆nxn (1) следует, что базисное решение x1=h1, x2=h2,...xm=hm, xm+1=0,...xn=0 (2) является оптимальным решением задачи ЛП L=c1x1+c2x2+...cnxn,при условиях:
x2 + g2,m+1 xm+1 +... + g2nxn = h2, ............ xm + gm,m+1 xm+1 +... + gmnxn = hm
и xj≥0, j = 1,2,...n, тогда и только тогда, когда в уравнении L=∆m+1xm+1+...+∆nxn=L0 среди коэффициентов ∆j при неизвестных нет ни одного положительного, т.е. условие оптимальности имеет вид: ∆j ≤0, j=1,2,...n. Действительно, если в общем решении xi=hi-gi,m+1xm+1-...-ginxn, i=1,2,...,m мы станем придавать различные неотрицательные значения свободным неизвестным так, чтобы соответствующие базисные неизв-е принимали неотрицательные значения, то одновременно с частными неотрицательными решениями с-мы ограничений будем получать согласно выражению (1), соответствующие им значения целевой ф-ии. В частности, при нулевых значениях свободных неизвестных получится базисное решение (2) и соответствующее ему значение линейной формы L0=c1h1+c2h2+...cmhm+cm+1*0+...+cn*0 = 17. Симплексный метод ЛП: условие единственности базисного оптимального решения. Условие неограниченности целевой ф-ии на множестве допустимых решений.
(1) L + Строго отрицательны. Если же хотя бы один из коэффициентов при свободных неизвестных равен нулю, то будут и небазисные оптимальные решения.
x1 + g1,m+1xm+1 +... + g1nxn = h1,
x2 + g2,m+1 xm+1 +... + g2nxn = h2, (2) ............ xm + gm,m+1 xm+1 +... + gmnxn = hm.
18. симплексный метод ЛП: переход от одного базисного допустимого решения к другому. Правила выбора разрешающей неизвестной и разрешающего уравнения, их обоснование. Монотонность и конечность симплексного алгоритма для невырожденной задачи ЛП, понятие о зацикливании. Тк неизвестная xs при нулевых значениях других свободных неизвестных не может возрастать неограниченно, а целевую ф-ю мы хотим минимизировать, то придадим неизвестной xs наибольше значение, которое она может принять, тем самым выделив из общего решения крайнее неотрицательное решение системы ограничений. Это крайнее решение совпадает с новым базисным неотрицательным решением, соответствующим новому предпочитаемому виду системы, для получения которого достаточно принять неизвестную xs за разрешающую и подвергнуть систему симплексному преобразованию. Если
Процесс перехода к новым и новым решениям продолжается до тех пор, пока не будет получено оптимальное решение (или не будет доказана неограниченность линейной формы на множестве решений системы ограничений, но это утверждение справедливо лишь при условии невырожденности задачи, т.е. ни на одном этапе процесса решения ни один из свободных членов системы ур-й не обращается в нуль. Новое значение линейной формы строго меньше предыдущего и через конечное число шагов мы придем к оптимальному решению (или докажем неразрешимость задачи). В вырожденном случае на одном или нескольких этапах свободный член может оказаться равны нулю, и значение линейной формы не измениться. Появится возможность цикла. 19. Метод искусственного базиса.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.57 (0.012 с.) |




 Откуда выразим базисные неизвестные через свободные неизвестные и правые части СЛАУ:
Откуда выразим базисные неизвестные через свободные неизвестные и правые части СЛАУ: 
 Предположим, что предприятие выпускает n видов продукции при использовании m видов ресурсов. Известны: технологическая матрица расходов iго вида ресурса на единицу jго вида продукции – (аij), где i=
Предположим, что предприятие выпускает n видов продукции при использовании m видов ресурсов. Известны: технологическая матрица расходов iго вида ресурса на единицу jго вида продукции – (аij), где i=  ; j=
; j= 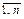 . Матрица запаса ресурсов B =
. Матрица запаса ресурсов B = cj xj
cj xj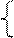 а11x1 + a12x2 + … a1nxn ≤ b1
а11x1 + a12x2 + … a1nxn ≤ b1

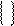
 а11 … а1n x1 b1
а11 … а1n x1 b1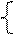 Основную задачу ЛП сформулируем следующим образом: даны система m линейных уравнений с n неизвестными
Основную задачу ЛП сформулируем следующим образом: даны система m линейных уравнений с n неизвестными Основной задачей линейного программиро-вания называется задача отыскания min ли-нейной формы z =
Основной задачей линейного программиро-вания называется задача отыскания min ли-нейной формы z = 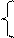 -z = -
-z = -  cj xj → min. И ограничения
cj xj → min. И ограничения
 C=(c1, …, cn).
C=(c1, …, cn).
 Минимизировать L=c1x1+c2x2+...cnxn (1), при условиях:
Минимизировать L=c1x1+c2x2+...cnxn (1), при условиях: ci hi (5).
ci hi (5).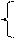 x1 + g1,m+1xm+1 +... + g1nxn = h1,
x1 + g1,m+1xm+1 +... + g1nxn = h1, При выполнении условия оптимальности базисное решение x1=h1, x2=h2,...xm=hm, xm+1=0,...xn=0 будет единственным оптимальным решением задачи ЛП тогда, и только тогда, когда все коэффициенты ∆m+1, ∆m+2,…, ∆n при свободных неизвестных в последнем уравнении вспомогательной системы xi +
При выполнении условия оптимальности базисное решение x1=h1, x2=h2,...xm=hm, xm+1=0,...xn=0 будет единственным оптимальным решением задачи ЛП тогда, и только тогда, когда все коэффициенты ∆m+1, ∆m+2,…, ∆n при свободных неизвестных в последнем уравнении вспомогательной системы xi + 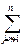 gijxj = hi, i= 1,2,...m,
gijxj = hi, i= 1,2,...m, Если есть хотя бы одна свободная неизвестная, такая что коэффициент ∆j при ней в последнем уравнении системы (1) положителен, а в первых m уравнениях той же системы среди коэффициентов g1j, g2j, …gmj при ней нет ни одного положительного, то задача линейного прогрмаммирования неразрешима в силу неограниченности линейной формы L=c1x1+c2x2+...cnxnна множестве неотрицательных решений системы ограничений
Если есть хотя бы одна свободная неизвестная, такая что коэффициент ∆j при ней в последнем уравнении системы (1) положителен, а в первых m уравнениях той же системы среди коэффициентов g1j, g2j, …gmj при ней нет ни одного положительного, то задача линейного прогрмаммирования неразрешима в силу неограниченности линейной формы L=c1x1+c2x2+...cnxnна множестве неотрицательных решений системы ограничений min
min  =
=  , то за разрешающее Ур-е берем r-е. как только мы получим новое базисное неотрицательное решение системы ограничений, придется это решение исследовать на оптимальность.
, то за разрешающее Ур-е берем r-е. как только мы получим новое базисное неотрицательное решение системы ограничений, придется это решение исследовать на оптимальность.


