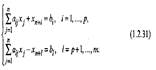Многомерные векторы и действия над ними. N-мерное векторное пространство.

Сов-ть n чисел а₁,а₂,…,а_n, заданных в определенном порядке,наз n-мерным вектором.Числа a_i наз компонентами или координатами вектора,число n -его размерностью.Обозначают вектор след образом: а(а₁,а₂,…,а_n) А(а₁,а₂,…,а_n).

∑ векторов a и b наз вектор а+b=(а₁+b₁,а₂+b₂,…,а_n+b_n) каждая компонента кот =сумме соотв-х компонент слагаемых векторов. Произведением вектора а на число λ наз вектор λа= (λа₁, λа₂,…, λа_n) каждая компонента кот равна произведению соотв компоненты вектора а на это число. Скалярным произведением двух векторов одной размерности a и b наз число,равное сумме попарных произведений соотв компонент векторов a и b. Скалярное произведение

(a,b)=a₁b₁+a₂b₂+…a_nb_n=∑a_ib_i.

Множество R эл-тов a,b,c,…наз линейным пространством,если:1)имеется правило,кот позволяет построить для кажд двух эл-тов a и b из R третий эл-т из R,называемый суммой эл-в a и b (a+b); 2) имеется правило,кот позволяет построить для кажд эл-та a из R и любого действительного числа λ эл-т а^| из R,наз-мый произведением эл-та а на число λ и обозначаемый λа; 3)сущ нулевой эл-т обозначаемый 0, обладающий свойством а+0=а, для каждого эл-та а сущ эл-т –а и облад-й св-вом а+(-а)=0; 4)правила образования суммы эл-в и произведения эл-в на число удовлетворяют условиям a+b=b+a, (a+b)+c=a+(b+c), λ(μa)=(μλ)a,1*a=a, 0*a=0*λ=0, (μ+λ)a=λa+ μa, λ(a+b)λa+λb. Множество всех n-мерных векторов-упорядоченных систем действительных чисел-образует линейное пространство в смысле данного определения.Его часто наз арифметическим n-мерным пространством.

 

 

6.Матрицы, их классификация. Сложение матриц и умножение матрицы на число,умножение матрицы на матрицу,свойства.

Матрицей размера mxn наз таблица чисел, кот расположена в m-строках и n-столбцах

a₁₁ а₁₂ …а_1n

А= a₂₁ а₂₂ …а_2n или кратко А=(a_ij)

…………..

a_m1 а_m2 …а_mn

Если т= п, то матрица называется квадратной матрицей n-го по­рядка. Кв. матрица наз треугольной, если все ее элемен­ты, стоящие над или под главной диагональю, равны нулю. Кв. матрица называется диагональной, если все ее эл-ты, стоящие на главной диагонали, отличны от нуля, а остальные равны нулю. Диагональная матрица наз единичной, если а_ii= 1, i =1,..., п. Транспонированной матрицей наз матрица, строки кот.заменены столбцами.Единичную матрицу принято обозначать буквой Е:

.

Суммой двух матриц одного размера называется матрица того же размера, каждый элемент которой равен сумме соответствующих эле­ментов матриц-слагаемых. Так, если А - || а_ij || и В=|| b_ij|| — матрицы размера т х п, то их суммой является матрица С = А + В, такая, что c_ij=a_ij+b_ij. Произведением матрицы А размера т х п на число А, называется матрица D того же размера, у которой d_ij=a_ijλ.. Для транспонированных матриц справедли­вы следующие соотношения: 1 )(А')' = A;

2)(АВ)' = В'А'; 3) (А + В)' = А' + В'.

Произведением матрицы А размера т х п на матрицу В размера n х k наз матрица С размера т х k, эл-ты кот с_ij равны скалярному произведению i-й строки матрицы А на_j-й столбец мат­рицы В, т.е.

Произведение матриц обозначается С = АВ. Скалярное произве­дение векторов а и b можно представить как произведение вектора-строки (матрицы-строки) а на вектор-столбец (матрицу-столбец) b ': (a, b) = ab'.Д ля операции произведения матриц справед­ливы следующие свойства: 1) A(BС) = (АВ)С; 2)(А + В)С = АС + ВС;
3)A(B+С)=AB+AC; 4) λАВ) = (λА)В.

 

 

7.Системы линейных алгебраических неравенств

Система т алгебраических неравенств первой степени с п неизвест­ными может быть записана в виде

Совокупность п чисел a₁,а.₂,,...,а_n, взятых в определенном поряд­ке, называется решением системы неравенств (1.2.30), если при под­становке этих чисел на место соответствующих неизвестных неравен­ства не нарушатся. Решение (<x_l5 a₂,..., а_/() системы неравенств назы­вается неотрицательным, если все а > 0. В этом случае,когда система имеет решение,она наз.совместной, в противном случае противоречивой или несовместной. Совместная система наз определенной или неопределенной в зависимости от того, имеет ли она одно или несколько решений. Две СЛАН с одинаковым числом неизвестных наз.эквивалентгыми или равносильными, если они имеют одни и те же решения, либо вообще не имеет решений. СЛАН часто преобразуют в СЛАУ путем введения дополнительных неотрицательных переменных (неизвестных) х_п+1, x_n+2 ,, х_n+m:

Исследование и решение системы т линейных неравенств с п неизвестными сводится к исследованию и решению соответствующей системы m линейных уравнений с п + т неизвестными. В частности, нахождение неотрица­тельных решений системы линейных неравенств (1.2.30) связано с по­иском неотрицательных решений системы линейных уравнений (1.2.31).Векторная форма записи СЛАУ: a₁x₁+a₂x₂+…+a_nx_n=b

Матричная: A*x=b