
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Но что же назвать риском всей игры.Содержание книги
Поиск на нашем сайте
Риск можно измерять по разному, как размах вариации R= как среднее линейное отклонение: М / Обычно считают среднее кавдратичное отклонение: r= В нашем случае риск: 35. Матричная игра как модель конкуренции и сотрудничества. Графическое решение игр с матрицей 2*n и m*2 доминирование чистых стратегий. Пусть, например, A= i j j i Видим, что седловой точки нет. Обозначим искомую оптимальную стратегию Первого (x, 1 – x). Обозначим nj(x) – средний выигрыш Первого в расчете на партию, когда он использует стратегию (x,1–x), а Второй – j-ю чистую стратегию. Имеем n1(x)=4x-2(1-x), n3(x)=-2x+(1-x). Возьмем на плоскости систему координат, по горизонтальной оси вправо отложим x, по вертикальной оси – значения функций nj(x). I n1(x)=6x-2 III n3(x)=-3x+1
Находим нижнюю огибающую семейства прямых. Отыщем ее высшую точку. Она и дает решение игры. Ее координаты определяются решением уравнения n1(x)=n3(x), откуда x*=1/3, n*=n2(x*)=n3(x*)=0. Таким образом, оптимальная стратегия Первого есть Р*=(1/3; 2/3), а цена игры n*= 0. Обозначим вероятность выбора Вторым первого столбца через y, а третьего столбца – через (1-y). Воспользуемся утверждением, что M(1;y*)=n*, т.е. 4y*-2(1-y*)= 0, откуда y*=1/3. Таким образом, оптимальная стратегия Второго Q*=(1/3;0, 2/3). Окончательный ответ следующий: оптимальная стратегия Первого – Р*=(1/3; 2/3), оптимальная стратегия Второго – Q*=(1/3;0, 2/3), цена игры n*= -1/2. Она достигается в пяти вариантах игры: 1) P*Q* 2) P1Q* 3) P2Q* 4) P*Q1 5) P*Q3 Где Pi i-я чистая стратегия Первого игрока, а Qj j-я чистая стратегия Второго игрока. Рассчитаем риски во всех эти случаях. Риски максимальны в 4) и 2); минимальны в 3) и 5). Соответственно 4) и 2) модели конкуренции, а 3) и 5) сотрудничества.
Если игроки договорятся играть по 3) или 5) вариантам то есть: 3) Первый игрок по 2-й чистой стратегии, а Второй по оптимальной стратегии или 4) Первый по оптимальной, а Второй по3-й чистой стратегии, то они смогут сократить риск игры по сравнению с оптимальными стратегиями (с 2 до
36. Матричная игра типа m*n. Критерий оптимальности стратегий. 37. Теорема о преобразовании матрицы игры, сохраняющем оптимальные стратегии игроков. 38. Основная теорема теории игр, выражение оптимальных стратегий игроков через решения пары двойственных задач ЛП. Математической моделью такого конфликта двух участников с противоположными интересами является игра с нулевой суммой. Участники это – игроки. Стратегия игрока – это выбор одного из множества возможных вариантов его действий. Рассмотрим конечные игры, в кот. множества стратегий игроков конечны; стратегии первого игрока пронумеруем от 1 до m, а стратегии второго игрока – от 1 до n. Если первый игрок выбрал свою i-ю стратегию, а второй игрок свою j-ю стратегию, то результатом такого совместного выбора будет платеж aij второго игрока первому. Таким образом, игра с нулевой суммой однозначно определяется платежной матрицей. Строки - соответствуют стратегиям первого игрока, столбцы -второго игрока. Игра происходит партиями.
П= а21 а22 а2n
аm1 аm2 аmn
Смешанной стратегий первого игрока называется вектор P (p1, p2,…pm), где все pi Если игроки применяют свои смешанные стратегии P (p1, p2,…pm) и Q (q1, q2,…qn) соответственно, Выигрыш первого: выигрыш aij Вероятность pi qj. То есть первый игрок с вероятностью pi gj. выигрывает aij.. Математическое ожидание выигрыша первого игрока равно М(P,Q)= Математическое ожидание с. в. Строка k доминирует над строкой i, если все элементы строки k не меньше соответствующих элементов строки i и хотя бы один строго больше. Доминируемую строку можно временно удалить, потому что в оптимальной стратегии ей будет соответствовать вероятность ноль. Столбец l доминирует над столбцом j, если все его элементы не больше соответствующих элементов столбца j, а хотя бы один строго меньше. Доминируемый столбец j можно временно удалить, т.к. в оптимальной стратегии 2-го игрока ей будет соответствовать вероятность ноль. Основная теорема теории матричных игр: В матричной игре с нулевой суммой у игроков есть оптимальные стратегии. Другими словами: Всякая матричная игра имеет седловую точку в смешанных стратегиях. 39. Игры с природой: основные понятия, матрицы рисков, критерии Вальда, Севиджа, Гурвица. Предположим, что лицо, принимающее решения может выбрать одну из возможных решений Если будет принято Неопределенная ситуация похожа на матричную игру, отличие состоит в том, что противником в данном случае является природа, цели которой не всегда противоположны нашим: они могут совпадать с целями ЛПР, а могут и не совпадать. Поэтому ситуация с неопределенностью называют еще играми с природой. В ситуации полной неопределенности могут быть высказаны лишь некоторые рекомендации предварительного характера. Они не обязательно будут приняты ЛПР. Многое будет зависеть, например, от его склонности к риску. Но как оценить риск в данной схеме? Допустим, мы хотим оценить риск, который несет
Значит, принимая Более широкое понятие – неопределенность. Ситуация полной неопределенности характеризуется отсутствием какой бы то ни было дополнительной информации. Правило Вальда (крайнего пессимизма): рекомендует принять такое решение i0 , что Правило Гурвица (взвешивающее пессимистический и оптимистический подходы к ситуации). Принимается решение
40. Многокритериальная оптимизация. Задачи многокритериальной, или векторной, оптимизации возникают в тех случаях, когда имеется несколько целей, которые не могут быть отражены одним критерием (стоимость, надежность и т.п.) Требуется найти точку области допустимых решений, которая максимизирует или минимизирует все эти критерии. Обозначим i-й частный критерий через В идеальном случае в этой задаче можно вести поиск такого решения, которое принадлежит пересечению множеств оптимальных решений однокритериальных задач. Однако указанное пересечение обычно оказывается пустым множеством, и потому приходится рассматривать переговорное множество решений Парето. Вектор х* Основной вопрос, который изучается в многокритериальной оптимизации, - формулировка подходящего обобщенного критерия в зависимости от конкретной ситуации. В некоторых случаях вместо одного обобщенного критерия и решения одной задачи скалярной оптимизации предлагается рассматривать последовательность задач скалярной оптимизации.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.235.85 (0.009 с.) |

 max -
max - 

 2
2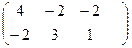 , тогда: В матрице А 3-й столбец доминирует 2-й, поэтому исключим 2-й столбец из рассмотрения: A’=
, тогда: В матрице А 3-й столбец доминирует 2-й, поэтому исключим 2-й столбец из рассмотрения: A’=  . Проверим, нет ли седловой точки, поскольку при ее наличии решение игры сразу ясно. max min aij = -2; min max aij= 1
. Проверим, нет ли седловой точки, поскольку при ее наличии решение игры сразу ясно. max min aij = -2; min max aij= 1

 ), при этом цена игры останется такой же, как если бы оба они играли по оптимальным стратегиям.
), при этом цена игры останется такой же, как если бы оба они играли по оптимальным стратегиям.
 а11 а21 а1n
а11 а21 а1n 0 (i=1,2,…,m), а
0 (i=1,2,…,m), а  p
p  =1. при этом p
=1. при этом p  - вероятность, с которой первый игрок выбирает вою i-ю стратегию. Аналогично определяются смешанные стратегии и Q (q1, q2,…qn)второго игрока. Чистая стратегия также попадает под определение смешанной – если все вероятности равны нулю, кроме одной, равной единице.
- вероятность, с которой первый игрок выбирает вою i-ю стратегию. Аналогично определяются смешанные стратегии и Q (q1, q2,…qn)второго игрока. Чистая стратегия также попадает под определение смешанной – если все вероятности равны нулю, кроме одной, равной единице. pi qj aij есть средний выигрыш. И это равно математическому ожиданию проигрыша второго игрока. Если игроки озабочены только максимизацией среднего дохода за партию игры то они будут играть со своими оптимальными стратегиями:
pi qj aij есть средний выигрыш. И это равно математическому ожиданию проигрыша второго игрока. Если игроки озабочены только максимизацией среднего дохода за партию игры то они будут играть со своими оптимальными стратегиями:  – Первый игрок и
– Первый игрок и  – второй, оптимальны стратегии если М(P,Q*)
– второй, оптимальны стратегии если М(P,Q*)  М(P*,Q*)
М(P*,Q*)  называется ценой игры, обозначим ее
называется ценой игры, обозначим ее  .
. . Ситуация является неопределенной, понятно лишь, что наличествует какой-то из вариантов
. Ситуация является неопределенной, понятно лишь, что наличествует какой-то из вариантов 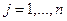 .
.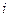 -e решение, а состояние внешней среды соответствует
-e решение, а состояние внешней среды соответствует  -й ситуации, то фирма, возглавляемая ЛПР, получит доход
-й ситуации, то фирма, возглавляемая ЛПР, получит доход  . Матрица
. Матрица  называется матрицей последствий (возможных решений).
называется матрицей последствий (возможных решений). .
. , а только
, а только  . Матрица
. Матрица  называется матрицей рисков.
называется матрицей рисков. Правило Сэвиджа (правило минимального риска): анализируется матрица рисков
Правило Сэвиджа (правило минимального риска): анализируется матрица рисков  , такое что
, такое что 
 где
где 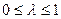 . Значение
. Значение  выбирается из субъективных соображений.
выбирается из субъективных соображений. I(x), а область допустимых решений через Q. Учитывая, что изменением знака функции всегда можно свести задачу минимизации к задаче максимизации и наоборот, можно сформулировать задачу векторной оптимизации следующим образом:
I(x), а область допустимых решений через Q. Учитывая, что изменением знака функции всегда можно свести задачу минимизации к задаче максимизации и наоборот, можно сформулировать задачу векторной оптимизации следующим образом: 
 max x
max x 
 Q называется эффективным решением, если не существует такого х
Q называется эффективным решением, если не существует такого х  что Z
что Z  (x*), i=1,2,.,m, причем хотя бы для одного i имеет место строгое неравенство. Множество допустимых решений, для которых невозможно одновременно улучшить все частные показатели эффективности, принято называть областью Парето или областью компромиссов, а принадлежащие ей решения – эффективными или оптимальными по Парето.
(x*), i=1,2,.,m, причем хотя бы для одного i имеет место строгое неравенство. Множество допустимых решений, для которых невозможно одновременно улучшить все частные показатели эффективности, принято называть областью Парето или областью компромиссов, а принадлежащие ей решения – эффективными или оптимальными по Парето.


