
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип оптимальности и реккурентные соотношения.Содержание книги
Поиск на нашем сайте
Принцип искать всегда оптимальное продолжение процесса относительно того состояния, которое достигнуто в данный момент, принято называть принципом оптимальности. Параметр состояние и ф-ия состояния. Состояние на каждом шаге характ-ся некоторой переменной величиной, кот. называется параметром состояния. Наилучший эффект на данном этапе вместе с уже рассмотренными шагами хар-ся функцией состояния. Решение конкретной задачи методом динамич. Программирования сводится к выбору параметра состояния, составлению ф-ии состояния и реекурентных соотношений, связывающих ф-ии состояния для двух соседних последовательных этапов, и их применению для выбора оптимального управления.
31. Задача распределения капитальных вложений: постановка, математическая модель и решение методом динамического программирования. Данная задача с n переменными представляется как многошаговый процесс принятия решений. На каждом шаге определяется экстремум функции только от одной переменной. Предположим, что указано n пунктов, где требуется построить или реконструировать предприятия одной отрасли, для чего выделено b рублей. Обозначим через fi(xi) прирост мощности или прибыли на j-м предприятии, если оно получит xi рублей капитальных вложений. Требуется найти такое распределение (x1,x2,..., xn) капитальных вложений между предприятиями, которое максимизирует суммарный прирост мощности или прибыли z = f1(x1) + f2(х2) +... + fn(xn) при ограничении по общей сумме капитальных вложений x1 + x2 +... + xn = b причем будем считать, что все переменные xj принимают только целые неотрицательные значения xj = 0, или 1, или 2, или 3,... Функции fj(xj) мы считаем заданными, заметив, что их определение - довольно трудоемкая экономическая задача. Воспользуемся методом динамического программирования для решения этой задачи. Динамическое программирование - это вычислительный метод для решения задач управления определенной структуры. Введем параметр состояния и определим функцию состояния. За параметр состояния x примем количество рублей, выделяемых нескольким предприятиям, а функцию состояния Fk(x) определим как максимальную прибыль на первых k предприятиях, если они вместе получают x рублей. Параметр x может изменяться от 0 до b. Если из x рублей k-е предприятие получит xk рублей, то каково бы ни было это значение, остальные x - xk рублей естественно распределить между предприятиями от первого до (k-1)-го так, чтобы была получена максимальная прибыль Fk-1(x - xk). Тогда прибыль k предприятий будет равна fk(xk) + Fk-1(x - xk). Надо выбрать такое значение xk между 0 и x, чтобы эта сумма была максимальной, и мы приходим к рекуррентному соотношению Fk(x)=max{ f k(x k) + Fk-1(x- x k)} 0 £ x k £ x для k = 2, 3, 4,..., n. Если же k=1, то F1(x) = f1(x) Рассмотрим пример. Пусть производственное объединение состоит из четырех предприятий (n=4). Общая сумма капитальных вложений равна 700 тыс. рублей (b=700), выделяемые предприятиям суммы кратны 100 тыс. рублей. Значения функций fj(xj) приведены в таблице 1, где, например, число 88 означает, что если третье предприятие получит 600 тыс. руб. капитальных вложений, то прирост прибыли на этом предприятии составит 88 тыс. руб. Таблица I
Прежде всего, заполняем табл. 2. Значения f2(x2) складываем со значениями F1(x - x2) = f1(x- x2) и на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение Продолжая процесс, табулируем функции F3(x), причем четвертому предприятию должно быть выделено х*4 = На долю остальных трех предприятий остается 400 тыс. руб. Из табл. 5 видно, что третьему предприятию должно быть выделено x*3 = Продолжая обратный процесс, находим x*2 = На долю первого предприятия остается x*1 = 700 - x*4 - x*3 - x*2 = 100 тыс. руб. Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям: x*1 =100; x*2 =100; x*3 = 200; x*4 = 300. Оно обеспечивает производственному объединению наибольший возможный прирост прибыли 155 тыс. руб. Студенту рекомендуется проверить выполнение равенства f1(x*1) + f2(x*2) + f3(x*3) + f4(x*4) = z max
Таблица 3
Таблица 5
Таблица 6
33. Матричная игра как модель конфликтной ситуации. Матричная игра двух лиц с нулевой суммой. Нижняя и верхняя цена игры, седловая точка. Чистые и смешанные стратегии игроков. В экономике часто встречаются ситуации, в которых сталкиваются 2 или более стороны, преследующие различные цели, причем результат, полученный каждой из сторон при реализации, причем результат, полученный каждой из сторон при реализации определенной стратегии, зависит от действий других сторон. Такие ситуации называются конфликтными. Например: борьба фирм за рынок сбыта, аукцион, спортивные состязания, карточная игра. Рассмотрим конфликт двух участников с противоположными интересами. Математической моделью такого конфликта является игра с нулевой суммой. Участники это – игроки. Стратегия игрока – это осознанный выбор одного из множества возможных вариантов его действий. Рассмотрим конечные игры, в кот. множества стратегий игроков конечны; стратегии первого игрока пронумеруем от 1 до m, а стратегии второго игрока – от 1 до n. Если первый игрок выбрал свою i-ю стратегию, а второй игрок свою j-ю стратегию, то результатом такого совместного выбора будет платеж aij второго игрока первому. Таким образом, игра с нулевой суммой однозначно определяется платежной матрицей.
а11 а21 а1n П= а21 а22 а2n
аm1 аm2 аmn
Строки - соответствуют стратегиям первого игрока, столбцы -второго игрока. Игра происходит партиями. Если выбор игрока не меняется от партии к партии – это чистая стратегия. У 1-го игрока m чистых стратегий, у 2-го n. При любой стратегии первого игрока, второй игрок будет выбирать стратегию обеспечивающий ему наибольший выигрыш, поэтому с точки зрения первого игрока надо выбирать такую стратегию, при которой второй игрок, действуя разумно заплатит наибольшую сумму. Такая стратегия первого игрока называется максиминной, а величина
Т.е. первый игрок, применяя свою максиминную стратегию обеспечивает себе выигрыш не меньше j i и соответствующая ей минимаксная стратегия второго игрока. То есть, принимая свою минимаксную стратегию второй игрок проиграет не больше Всегда
34. Ряд распределения выигрышей в матричной игре. Средний ожидаемый выигрыш и риск. Оптимальные стратегии игроков и цена игры. Смешанной стратегий первого игрока называется вектор P (p1, p2,…pm), где все pi Пусть игроки – Первый и Второй, играют в матричную игру с матрицей
Если игроки применяют свои смешанные стратегии P (p1, p2,…pm)и Q (q1, q2,…qn) соответственно, Выигрыш первого: выигрыш aij Вероятность pi qj. То есть первый игрок с вероятностью pi gj. выигрывает aij.. Математическое ожидание выигрыша первого игрока равно М(P,Q)=
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.183.161 (0.007 с.) |

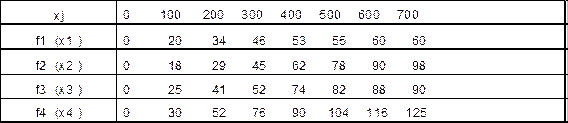
 . Заполняем таблицу 3.
. Заполняем таблицу 3. (x) и т.д. В табл. 6 заполняем только одну диагональ для значения x= 700. Наибольшее число на этой диагонали: Zmax = 155 тыс. руб.,
(x) и т.д. В табл. 6 заполняем только одну диагональ для значения x= 700. Наибольшее число на этой диагонали: Zmax = 155 тыс. руб., 4 (700) = 300 тыс. руб.
4 (700) = 300 тыс. руб. Таблица 2
Таблица 2 0 20* 34 46 53 55 60 60
0 20* 34 46 53 55 60 60
 (x)
(x)
 Таблица 4
Таблица 4 0
0



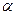 =
=  max min aij называется нижней ценой игры.
max min aij называется нижней ценой игры. =min max a ij
=min max a ij . Если
. Если  , то игра имеет седловую точку. При этом цена игры:
, то игра имеет седловую точку. При этом цена игры:  =
=  0 (i=1,2,…,m), а
0 (i=1,2,…,m), а  p
p  =1. при этом p
=1. при этом p  - вероятность, с которой первый игрок выбирает вою i-ю стратегию. Аналогично определяются смешанные стратегии и Q (q1, q2,…qn)второго игрока. Чистая стратегия также попадает под определение смешанной – если все вероятности равны нулю, кроме одной, равной единице.
- вероятность, с которой первый игрок выбирает вою i-ю стратегию. Аналогично определяются смешанные стратегии и Q (q1, q2,…qn)второго игрока. Чистая стратегия также попадает под определение смешанной – если все вероятности равны нулю, кроме одной, равной единице. . Пусть стратегия Первого есть
. Пусть стратегия Первого есть  , а Второго –
, а Второго –  . Тогда выигрыш Первого есть случайная величина (с.в.)
. Тогда выигрыш Первого есть случайная величина (с.в.)  с рядом распределения:
с рядом распределения: pi qj aij есть средний выигрыш.
pi qj aij есть средний выигрыш.


