
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Віддаль між двома заданими точкамиСодержание книги Поиск на нашем сайте
Віддаль між двома заданими точками Для будь-яких точок A (a) і B (b) координатної прямої відстань AB дорівнює модулю різниці координат цих точок, тобто 6.Властивості визначників: 1) det А=йЛ Ат, тобто визначник не змінюється при транспонуванні матриці; 2) якщо одна стрічка визначника складається лише з нупів, то визначник рівний иупю (те ж саме відноситься до стовпця); 3) при перестановці двох стрічок (стовпців) місцями визначник змінює знак; 4) визначник, що містить дві однакові стрічки (стовпці) рівний нупю; 5) якщо всі елементи деякої стрічки визначника помножиги на довільне число к то сам визначник помножиться на це ж число; наслідок: спільний множник всіх елементів стрічки або стовпця можна винес-ти за знак визначника; 6) визначник, який містить дві пропорційні стрічки (стовгщі) рівний нупю; 7) якщо до елементів однієї стрічки (стовпця) додати елементи ішпої (можливо домножені на деякий коефіцієнт), то визначник не зміниться; 8) визначник трикугної матриці рівний добугку елементів, які розміщені на го-ловнійдіагоналі матрщі; 9) визначник добугку матрщь рівний добугку визначників матриць
7. Геометричний зміст похідної v(t) = S'(t).
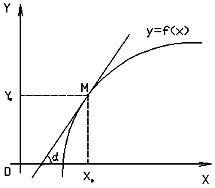
8. Горизонтальна асимптота - пряма виду Горизонтальна асимптота є частковим випадком похилої при k = 0. Дослідження асимптот дозволяє чіткіше уявити поведінку графіка функції, оскільки властивості функції поблизу її асимптоти дуже близькі до властивостей асимптоти — лінійної функції, властивості якої добре вивчені. Систематичне використання цієї властивості породило напрямок у сучасній математиці — «асимптотичні методи дослідження». 9. Матриця — математичний об'єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця) і допускаючий операції (додавання, віднімання, множення та множення на скаляр). Зазвичай матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці непрямокутної форми. В даній статті вони розглядатися не будуть. Горизонтальні лінії в матриці звуть рядками, вертикальні — стовпцями. Матрицю, що складається з m рядків та n стовпців, називають матрицею m -на- n (або mn -матрицею), а m і n — її розмірністю. Елемент матриці A, що знаходиться на перетині i -го рядка з j -им стовпчиком, називають i,j -им елементом або (i, j)-им елементом A. Записують це як Ai,j чи A [i,j], або, в нотації мови програмування C, A[i][j]. Часто пишуть Додавання Якщо дано дві матриці m -на- n A і B, можемо означити їх суму A + B як матрицю m -на- n, що утворюється додаванням відповідних елементів, себто,
Множення на скаляр Якщо дано матрицю A і число c, можемо означити множення на скаляр cA як (cA)[ i, j ] = cA [ i, j ]. Наприклад,
З цими двома операціями множина M(m, n, R) усіх матриць m -на- n з дійсними елементами є дійсним векторним простором розмірності mn. Множення матриць Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m -на- n (m рядків, n стовпчиків), а B — матриця n -на- p (n рядків, p стовпчиків), їх добуток AB є матрицею m -на- p (m рядків, p стовпчиків), що розраховується за формулою: (AB)[ i, j ] = A [ i, 1] * B [1, j ] + A [ i, 2] * B [2, j ] +... + A [ i, n ] * B [ n, j ] для кожної пари i та j.
10. Визначник — одна з найважливіших характеристик квадратних матриць. Визначник 2×2 матриці Щоб знайти визначник
Дати означення мінору довільного елемента визначника n-порядку. Мінором Mij визначника n-порядку назв. визначник n-1 порядку, який отриманий з початкового шляхом ви креслення i-го рядка та j-го стовпчика. Знаходження координат вектора за відомими координатами початку та вершини. Відрізок, у якому точка A – початок, а точка B – вершина, наз. вектором. Нехай A (x1;y1), a B (x2;y2), то АВ(вектор) = (x2-x1; y2-y1) Означення
Приклад незростаючої функції Нехай дано функцію § функція f називається зроста́ючою на M, якщо
§ функція f називається стро́го зроста́ючою на M, якщо
§ функція f називається спадною на M, якщо
§ функція f називається стро́го спадною на M, якщо
Приклад неспадної функції (Строго) зростаюча чи спадна функція називається (строго) монотонною 28.Основні види матриць
Визначення матриці. Матрицею називається прямокутна таблиця з чисел, що містить деяку кількість m рядків і деяку кількість n стовпців. Основні поняття матриці: Числа m і n називаються порядками матриці. У випадку, якщо m = n, матриця називається квадратною, а число m = n - їїпорядком. У подальшому для запису матриці будуть застосовуватися позначення:
Хоча іноді в літературі зустрічається позначення:
Втім, для короткого позначення матриці часто використовується одна великабуква латинського алфавіту, (наприклад, А), або символ | | aij | |, а іноді і зроз'ясненням: A = | | aij | | = (aij) (i = 1, 2,..., m; j = 1,2,... n) Числа aij, що входять до складу даної матриці, називаються її елементами. У записі aij перший індекс i означає номер рядка, а другий індекс j - номерстовпця. Наприклад, матриця
це матриця порядку 2 × 3, її елементи a11 = 1, a12 = x, a13 = 3, a21 =- 2y,... Отже, ми ввели визначення матриці. Розглянемо види матриць і дамовідповідні до них визначення.
Види матриць Введемо поняття матриць: квадратних, діагональних, одиничних і нульових. Визначення матриці квадратної: Квадратної матрицею n-го порядку називаєтьсяматриця розміру n × n. У разі квадратної матриці
вводяться поняття головної і побічної діагоналей. Головною діагоналлю матриціназивається діагональ, що йде з лівого верхнього кута матриці в правий нижнійїї кут.
Побічної діагоналлю тієї ж матриці називається діагональ, що йде з лівогонижнього кута в правий верхній кут.
Поняття діагональної матриці: діагональної називається квадратна матриця, у якої всі елементи поза головною діагоналі дорівнюють нулю.
Одиничної (позначається Е іноді I) називається діагональна матриця з одиницями на головній діагоналі.
Означення розв’язку СЛАР. Розв'язати систему СЛАР – значить знайти такі значення невідомих Таблиця похідних елементарних функцій.
Теорема Кронеккера-Капеллі.
СЛАР має розв'язки тоді і тільки тоді,коли ранг її матриці Причому система має єдине рішення, якщо ранг дорівнює числу невідомих і нескінченно багато рішень, якщо ранг менше числа невідомих. Точки перегину функції. В математиці, точкою перегину, плоскої кривої називається точка кривої в якій змінюється знак кривизни. Якщо крива є графіком функції, то в цій точці опукла частина функції відділяється від вгнутої. Властивості
78.Скалярним добутком двох векторів називається число яке дорівнює сумі добутків відповідних кординат. 79. Два вектори ортогональні, якщо скалярний добуток цих векторів дорівнює нулю, тобто, кут між ними 90° або π/2 радіан. Таким чином, ортогональність векторів є узагальненням перпендикулярності. Умови паралельності прямих Теорема 1. Якщо при перетині двох прямих третьою виконується хоча б одна з таких умов: Фізичний зміст похідної Похідна від шляху-швидкість 83. 84. Система рівнянь називається сумісною, якщо вона має принаймні один розв’язок, і несумісною, якщо вона не має розв’язків. Система рівнянь називається визначеною, якщо вона має лише один розв’язок, і невизначеною, якщо вона має безліч розв’язків.
Віддаль між двома заданими точками Для будь-яких точок A (a) і B (b) координатної прямої відстань AB дорівнює модулю різниці координат цих точок, тобто 6.Властивості визначників: 1) det А=йЛ Ат, тобто визначник не змінюється при транспонуванні матриці; 2) якщо одна стрічка визначника складається лише з нупів, то визначник рівний иупю (те ж саме відноситься до стовпця); 3) при перестановці двох стрічок (стовпців) місцями визначник змінює знак; 4) визначник, що містить дві однакові стрічки (стовпці) рівний нупю; 5) якщо всі елементи деякої стрічки визначника помножиги на довільне число к то сам визначник помножиться на це ж число; наслідок: спільний множник всіх елементів стрічки або стовпця можна винес-ти за знак визначника; 6) визначник, який містить дві пропорційні стрічки (стовгщі) рівний нупю; 7) якщо до елементів однієї стрічки (стовпця) додати елементи ішпої (можливо домножені на деякий коефіцієнт), то визначник не зміниться; 8) визначник трикугної матриці рівний добугку елементів, які розміщені на го-ловнійдіагоналі матрщі; 9) визначник добугку матрщь рівний добугку визначників матриць
7. Геометричний зміст похідної v(t) = S'(t).
8. Горизонтальна асимптота - пряма виду Горизонтальна асимптота є частковим випадком похилої при k = 0. Дослідження асимптот дозволяє чіткіше уявити поведінку графіка функції, оскільки властивості функції поблизу її асимптоти дуже близькі до властивостей асимптоти — лінійної функції, властивості якої добре вивчені. Систематичне використання цієї властивості породило напрямок у сучасній математиці — «асимптотичні методи дослідження». 9. Матриця — математичний об'єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця) і допускаючий операції (додавання, віднімання, множення та множення на скаляр). Зазвичай матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці непрямокутної форми. В даній статті вони розглядатися не будуть. Горизонтальні лінії в матриці звуть рядками, вертикальні — стовпцями. Матрицю, що складається з m рядків та n стовпців, називають матрицею m -на- n (або mn -матрицею), а m і n — її розмірністю. Елемент матриці A, що знаходиться на перетині i -го рядка з j -им стовпчиком, називають i,j -им елементом або (i, j)-им елементом A. Записують це як Ai,j чи A [i,j], або, в нотації мови програмування C, A[i][j]. Часто пишуть Додавання Якщо дано дві матриці m -на- n A і B, можемо означити їх суму A + B як матрицю m -на- n, що утворюється додаванням відповідних елементів, себто,
Множення на скаляр Якщо дано матрицю A і число c, можемо означити множення на скаляр cA як (cA)[ i, j ] = cA [ i, j ]. Наприклад,
З цими двома операціями множина M(m, n, R) усіх матриць m -на- n з дійсними елементами є дійсним векторним простором розмірності mn. Множення матриць Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m -на- n (m рядків, n стовпчиків), а B — матриця n -на- p (n рядків, p стовпчиків), їх добуток AB є матрицею m -на- p (m рядків, p стовпчиків), що розраховується за формулою: (AB)[ i, j ] = A [ i, 1] * B [1, j ] + A [ i, 2] * B [2, j ] +... + A [ i, n ] * B [ n, j ] для кожної пари i та j.
10. Визначник — одна з найважливіших характеристик квадратних матриць. Визначник 2×2 матриці Щоб знайти визначник
|
||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.199.240 (0.008 с.) |

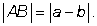
 за умови існування межі
за умови існування межі  .
. для означення матриці A розмірності n x m, де кожен елемент матриці A [i,j] позначають як aij для всіх 1 ≤ i ≤ n та 1 ≤ j ≤ m.
для означення матриці A розмірності n x m, де кожен елемент матриці A [i,j] позначають як aij для всіх 1 ≤ i ≤ n та 1 ≤ j ≤ m.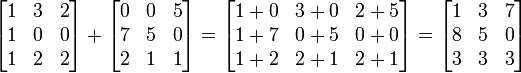
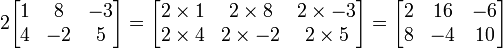
 матриці, множимо елементи головної діагоналі та віднімаємо добуток елементів побічної діагоналі:
матриці, множимо елементи головної діагоналі та віднімаємо добуток елементів побічної діагоналі: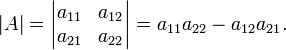

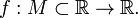 Тоді
Тоді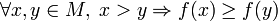 .
.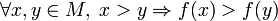 .
.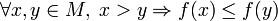 .
.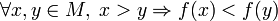 .
.


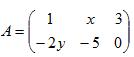
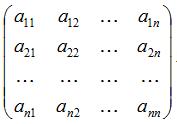
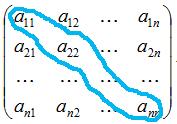

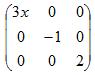

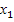 =
=  ,
, 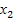 =
= 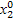 ,....
,.... 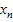 =
= 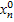 , при підстановці яких у систему СЛАР усі її рівняння обертаються у тотожність.
, при підстановці яких у систему СЛАР усі її рівняння обертаються у тотожність.
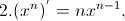


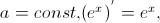








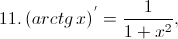


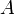 дорівнює рангу її розширеної матриці
дорівнює рангу її розширеної матриці 

 ;
;


