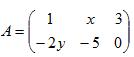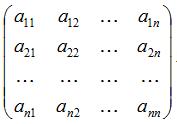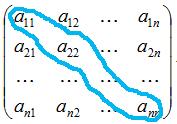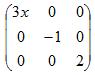Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знаходження оберненої матриці через союзну.Содержание книги
Поиск на нашем сайте
Сою́зною (приє́днаною) до матриці A, називається матриця створена з алгебраїчних доповнень для відповідних елементів первісної матриці, і транспонована потому.
Обернена Матриця обчислюється за формулою A-1 = A*/det A (det A – визначник матриці)
21.Канонічне рівняння площини в просторі:
22.Канонічне рівнянн прямої в 3-вимірному просторі
23. Колінеарні вектори, зв'язок між ними. Нехай 1. Колінеарність - відношення еквівалентності, тобто воно рефлексивно: 2. симметрично: 3. транзитивній: § Нулевий вектор колінеарний будь якому вектору: § Скалярний добуток векторів колінеарних дорівнює добутку довжин векторів
§ Вектори на площині колінеарні тоді і тільки тоді, коли їх Псевдоскалярний добуток дорівнює Колінеарні вектори лінійно залежні § Існує дійсне число § На площині 2 неколінеарних вектора
Два ненульових (не рівних 0) вектора називаються колінеарними, якщо вони лежать на паралельних прямих або на одній прямій. Припустимо, але не рекомендується синонім - «паралельні» вектори. Колінеарні вектори можуть бути однаково спрямовані («направлені») або протилежно направлені (в останньому випадку їх іноді називають «антиколлінеарнимі» або«антипаралельними»).
24.Критичні точки функції. Критичною точкою диференційовної функції Значення функції в критичній точці називається критичним значенням. Згідно з лемою Сарда, множина критичних значень будь-якої
Поняття критичної точки допускає узагальнення на випадок диференційовних відображень Критичні точки функцій і відображень грають важливу роль в таких галузях математики, як диференціальні рівняння, варіаційне числення, теорія стійкості, а також в механіці і фізиці. Дослідження критичних точок гладких відображень становить одне з основних питань теорії катастроф. Поняття критичної точки узагальнюється також на випадок функціоналів, визначених на нескінченновимірних функціональних просторах. Пошук критичних точок таких функціоналів є важливою частиною варіаційного обчислення. Критичні точки функціоналів (які, у свою чергу, є функціями) називаються екстремалями.
25.Кут між двома векторами
26. Кут між двома прямими в просторі.Умови паралельності та перпендикулярності.Кут між двома прямими і, заданих рівняннями визначається як кут між їх направляючими векторами та тому,
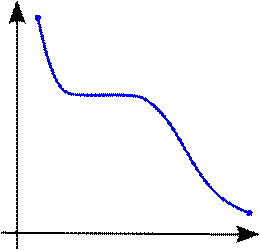
27 Монотонні функції. Моното́нна фу́нкція — це функція, приріст якої не змінює знаку, тобто завжди або невід’ємний, або недодатній. Якщо при цьому приріст ще і не дорівнює нулю, то функція називається стро́го моното́нною. Означення
Приклад незростаючої функції Нехай дано функцію § функція f називається зроста́ючою на M, якщо
§ функція f називається стро́го зроста́ючою на M, якщо
§ функція f називається спадною на M, якщо
§ функція f називається стро́го спадною на M, якщо
Приклад неспадної функції (Строго) зростаюча чи спадна функція називається (строго) монотонною 28.Основні види матриць
Визначення матриці. Матрицею називається прямокутна таблиця з чисел, що містить деяку кількість m рядків і деяку кількість n стовпців.
Основні поняття матриці: Числа m і n називаються порядками матриці. У випадку, якщо m = n, матриця називається квадратною, а число m = n - їїпорядком. У подальшому для запису матриці будуть застосовуватися позначення:
Хоча іноді в літературі зустрічається позначення:
Втім, для короткого позначення матриці часто використовується одна великабуква латинського алфавіту, (наприклад, А), або символ | | aij | |, а іноді і зроз'ясненням: A = | | aij | | = (aij) (i = 1, 2,..., m; j = 1,2,... n) Числа aij, що входять до складу даної матриці, називаються її елементами. У записі aij перший індекс i означає номер рядка, а другий індекс j - номерстовпця. Наприклад, матриця
це матриця порядку 2 × 3, її елементи a11 = 1, a12 = x, a13 = 3, a21 =- 2y,... Отже, ми ввели визначення матриці. Розглянемо види матриць і дамовідповідні до них визначення.
Види матриць Введемо поняття матриць: квадратних, діагональних, одиничних і нульових. Визначення матриці квадратної: Квадратної матрицею n-го порядку називаєтьсяматриця розміру n × n. У разі квадратної матриці
вводяться поняття головної і побічної діагоналей. Головною діагоналлю матриціназивається діагональ, що йде з лівого верхнього кута матриці в правий нижнійїї кут.
Побічної діагоналлю тієї ж матриці називається діагональ, що йде з лівогонижнього кута в правий верхній кут.
Поняття діагональної матриці: діагональної називається квадратна матриця, у якої всі елементи поза головною діагоналі дорівнюють нулю.
Одиничної (позначається Е іноді I) називається діагональна матриця з одиницями на головній діагоналі.
|
||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.84.174 (0.01 с.) |



 — вектори простору
— вектори простору 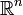 . Тоді вірні такі твердження:
. Тоді вірні такі твердження:

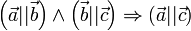

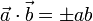 ) (взятих зі знаком «-», якщо вектори протилежно спрямовані)
) (взятих зі знаком «-», якщо вектори протилежно спрямовані)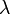 таке, щоо
таке, щоо 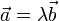 для колінеарних
для колінеарних 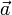 и
и 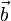 , за виключенням особливоого випадку
, за виключенням особливоого випадку  . Це означення а також критерій колінеарності.
. Це означення а також критерій колінеарності.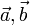 утворюють базис. Це означає, що будь-який вектор
утворюють базис. Це означає, що будь-який вектор 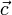 можна представити у вигляді:
можна представити у вигляді: 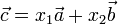 . Тоді
. Тоді 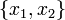 будуть координатами
будуть координатами 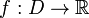 , де
, де  — область в
— область в 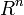 , називається точка, в якій всі її часткові похідні дорівнюють нулю. Ця умова еквівалентна рівності нулю диференціала функції в даній точці, а також рівносильна горизонтальності дотичної до графіка функції гіперплощини. Ця умова є необхідною (але не достатньою) для того, щоб внутрішня точка області могла бути точкою локального мінімуму або максимуму функції.
, називається точка, в якій всі її часткові похідні дорівнюють нулю. Ця умова еквівалентна рівності нулю диференціала функції в даній точці, а також рівносильна горизонтальності дотичної до графіка функції гіперплощини. Ця умова є необхідною (але не достатньою) для того, щоб внутрішня точка області могла бути точкою локального мінімуму або максимуму функції.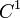 -гладкої функції
-гладкої функції 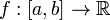 має нульову міру Лебега (хоча критичних точок при цьому може бути скільки завгодно, наприклад, для функції f = const будь-яка точка є критичною).
має нульову міру Лебега (хоча критичних точок при цьому може бути скільки завгодно, наприклад, для функції f = const будь-яка точка є критичною).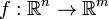 , і на випадок диференційовних відображень довільних многовиді
, і на випадок диференційовних відображень довільних многовиді 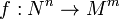 . У цьому випадку визначення критичної точки полягає в тому, що ранг матриці Якобі відображення f у ній менший максимального можливого (що дорівнюєmin{ n, m }).
. У цьому випадку визначення критичної точки полягає в тому, що ранг матриці Якобі відображення f у ній менший максимального можливого (що дорівнюєmin{ n, m }).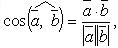


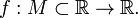 Тоді
Тоді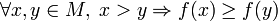 .
.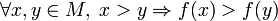 .
.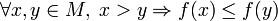 .
.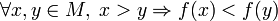 .
.