
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування визначеного інтегралаСтр 1 из 5Следующая ⇒
З М І С Т Розділ 1 Визначений інтеграл 1.1. Означення визначеного інтеграла як границі інтегральної суми. Умови існування та властивості визначеного інтеграла……………………5 1.2. Обчислення визначених інтегралів……………………………………………8 1.2.1. Формула Ньютона-Лейбніца…………………………………………………8 1.2.2. Метод заміни змінної………………………………………………………..12 1.2.3. Інтегрування частинами……………………………………………………..19
Розділ 2 Невласні інтеграли 2.1. Невласні інтеграли першого роду (з нескінченними межами)………..23 2.2. Невласні інтеграли другого роду (від необмежених функцій)…………..33
Розділ 3 Застосування визначеного інтеграла До задач геометрії 3.1. Обчислення площ плоских фігур…………………………………………. 43 3.2. Обчислення довжини дуги плоскої кривої………………………………. 56 3.3. Обчислення об’ємів тіл обертання………………………………………… 65 3.4. Обчислення площі поверхні тіл обертання……………………………… 73
ЛІТЕРАТУРА ………………………………………………………………… 84
Вступ Основна форма навчання студентів – самостійна робота над навчальним матеріалом, яка складається з вивчення теоретичних положень за підручником, розгляду прикладів і розв’язання задач. При вивченні матеріалу за підручником треба переходити до наступного питання тільки після правильного зрозуміння попереднього, виконуючи на папері усі обчислення, навіть і ті, які пропущені у підручнику. Розв’язання задач при вивченні дисципліни «Вища математика» часто пов’язано з багатьма складностями. Якщо складається скрутне становище при розв’язанні задачі, то треба вказати характер цього утруднення, привести припущення відносно плану розв’язку. Відомо, що при самостійному розв’язуванні задач студентам потрібні постійні консультації щодо способів їх розв’язування, оскільки знайти шлях до розв’язування задачі без допомоги викладача або відповідного підручника студентові не під силу. Допомогти студентам технічних спеціальностей всіх форм навчання подолати ці складності, навчити їх застосовувати теоретичні знання до розв’язування задач - основне призначення цього навчального посібника. У третій частині навчального посібника викладено матеріал з таких розділів вищої математики: «Визначений інтеграл», «Невласні інтеграли» та «Застосування визначеного інтеграла до задач геометрії». Основні теоретичні положення, формули та теореми ілюструються докладним розв’язанням великої кількості задач різного ступеня складності з їх повним аналізом. Для ефективності засвоєння матеріалу пропонуються завдання для самостійної роботи.
Автори сподіваються, що саме така побудова посібника надає студентові широкі можливості до активної самостійної роботи, яка, безумовно, сприятиме засвоєнню матеріалу при вивченні дисципліни «Вища математика».
Розділ 1 ВИЗНАЧЕНИЙ ІНТЕГРАЛ Означення визначеного інтеграла як границі інтегральної суми. Умови існування та властивості визначеного інтеграла Нехай функція
Сукупність точок
Означення 1. Якщо існує скінченна границя інтегральної суми
Числа
Означення 2. Функція
Геометричний зміст визначеного інтеграла полягає в тому, що визначений інтеграл від невід’ємної та інтегровної на відрізку
Рис.1.1 Необхідною умовою існування визначеного інтеграла є обмеженість функції Достатньою умовою існування визначеного інтеграла є неперервність функції
Розглянемо деякі властивості визначеного інтеграла: 1) Визначений інтеграл не залежить від позначення змінної інтегрування:
2) Визначений інтеграл з однаковими межами інтегрування дорівнює нулю:
3) Для будь-якого довільного сталого числа
4) При переставленні меж інтегрування визначений інтеграл змінює знак, тобто
5) Якщо функції
6) Якщо функція
7) Якщо функція
Аналогічно маємо, що
8) Якщо функції
9) Якщо функція
10) Якщо функція
11) Якщо функція
Це ствердження має назву теореми про середнє значення визначеного інтеграла. Формула Ньютона-Лейбніца Для пошуку способу обчислення визначеного інтеграла встановимо зв’язок між невизначеним та визначеним інтегралами. Для цього розглянемо Цей інтеграл називають визначеним інтегралом із змінною верхньою межею. Очевидно, він є функцією від Має місце наступна теорема Барроу: Якщо функція
Тобто для всякої неперервної на Ефективний і простий спосіб обчислення визначеного інтеграла дається формулою Ньютона-Лейбніца:
де
Зразки розв’язування задач Обчислити інтеграли. 1.
Первісною від даної підінтегральної функції є Розв’язування може бути подане у вигляді:
2.
3.
4.
5.
6.
Первісну можна знайти, використавши формулу пониження степеня:
7.
Для знаходження первісної в знаменнику виділимо повний квадрат.
8.
Знайдемо первісну функції. Для цього правильний дріб
Звільнившись від знаменника, маємо:
Отже,
Тоді
Завдання для самостійної роботи Обчислити інтеграли:
1. 2. 3. 4. 5. 6. Зразки розв’язування задач Обчислити інтеграли.
1.
Зробимо заміну Визначимо нові межі інтегрування. Якщо Отримаємо:
2. Використаємо властивість 4 і змінюємо межі інтегрування:
3.
4.
5.
6.
7.
Оскільки підінтегральна функція є раціональною відносно Тоді
8.
Перетворимо вираз Інтеграл набуває вигляду:
9. Підінтегральний вираз містить Отже, при при
Будемо мати: Щоб проінтегрувати парну степінь
Тобто
10.
Застосуємо для інтегрування тригонометричну підстановку
Межі інтегрування: при Отже,
Отриманий інтеграл не є табличним. Для його обчислення необхідно скористатися ще однією заміною. Позначимо При
Тоді
Завдання для самостійної роботи Обчислити інтеграли:
1. 2. 3. 4. 5. 6. 7. Зразки розв’язування задач Обчислити інтеграли.
1. Покладемо
2.
3.
4.
5.
Для обчислення отриманого інтегралу використаємо метод інтегрування частинами ще раз.
Після двократного інтегрування частинами ми прийшли до вихідного інтегралу. Позначимо
Таким чином отримали:
6.
Перший доданок можна обчислювати, а до другого знову застосуємо метод інтегрування частинами:
Завдання для самостійної роботи Обчислити інтеграли:
1. 2. 3. 4. 5.
Розділ 2 НЕВЛАСНІ ІНТЕГРАЛИ Зразки розв’язування задач Зразки розв’язування задач Розділ 3 ДО ЗАДАЧ ГЕОМЕТРІЇ Зразки розв’язування задач Розв’язання Побудуємо дані лінії і визначимо фігуру, площу якої треба знайти.
Площа визначається за формулою (3.1):
 
2.
Розв’язання Зобразимо фігуру, площу якої шукаємо.
Тоді
3.
Розв’язання
Фігура обмежена параболою
Як бачимо, фігура симетрична відносно осі Будемо мати:
4. Розв’язання Побудуємо дані лінії.
5.
Розв’язання Побудуємо параболу
Отже, парабола
6.
Канонічний вид параболи
Парабола симетрична відносно прямої
За формулою (3.4) знайдемо площу:
7. Розв’язання Побудуємо дані гіперболу та пряму.
Отже,
8. Розв’язання Побудуємо дані лінії.
Як бачимо, фігура розташована у I чверті, тому оберемо А саме: де Отримаємо:
Перейдемо до розглядання прикладів обчислення площ у параметричній системі координат для циклоїди та кардіоїди. Обидві ці криві мають механічне походження та описуються точкою кола радіуса
9. Знайти площу фігури обмеженої віссю
Розв’язання Поглянемо на вигляд цієї кривої.
Параметр
Таким чином, площа однієї арки циклоїди втричі більше площі кола, що котиться.
10. Знайти площу, обмежену кардіоїдою
Розв’язання
Наведемо вигляд цієї кривої.
Для обчислення площі використаємо формулу (3.6).
Обчислимо Тоді
Отримаємо:
Тепер ознайомимося із цікавими кривими у полярній системі координат.
11. Обчислити площу, обмежену лемніскатою Бернуллі Розв’язання
Прослідкуємо, як змінюється кут При Таким чином, на чверті площі полярний кут змінюється в межах від
Вся площа
12.Обчислити площу однієї пелюстки рози, яка задається рівнянням Зауваження. Зазначимо, що криві задані рівняннями Щоб знайти площу однієї пелюстки, визначимо, як змінюється полярний кут Нехай
|
|||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 750; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.246.254 (0.297 с.) |
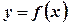 визначена на відрізку
визначена на відрізку  ,
,  <
<  . Розіб’ємо відрізок
. Розіб’ємо відрізок  довільних частин так, щоб
довільних частин так, щоб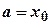 <
<  <
<  …<
…<  <
<  <
<  <…<
<…<  .
.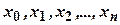 назвемо
назвемо  -розбиттям відрізка
-розбиттям відрізка  та значення функції
та значення функції  у довільній точці
у довільній точці  . Позначимо через
. Позначимо через  - найбільшу довжину серед довжин частинних відрізків, тобто
- найбільшу довжину серед довжин частинних відрізків, тобто 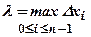 . Утворимо суму
. Утворимо суму  , яка називається інтегральною сумою функції
, яка називається інтегральною сумою функції  на відрізку
на відрізку  .
. при умові, що найбільша із різниць
при умові, що найбільша із різниць  прямує до нуля, яка не залежить ані від способу розбиття відрізка
прямує до нуля, яка не залежить ані від способу розбиття відрізка  у кожному з частинних відрізків, то вона називається визначеним інтегралом функції
у кожному з частинних відрізків, то вона називається визначеним інтегралом функції  . Отже, згідно з означенням,
. Отже, згідно з означенням, .
. - підінтегральним виразом;
- підінтегральним виразом;  - змінною інтегрування, а відрізок
- змінною інтегрування, а відрізок  ,
,  та віссю
та віссю  :
:
 .
. .
. справджується рівність:
справджується рівність: .
. .
. - інтегровні на відрізку
- інтегровні на відрізку  також є інтегровною на цьому відрізку, причому
також є інтегровною на цьому відрізку, причому .
. ,
,  , то вона інтегровна і в двох інших і для будь-якого взаємного розташування точок
, то вона інтегровна і в двох інших і для будь-якого взаємного розташування точок  має місце рівність
має місце рівність
 .
. <
< 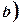 і всюди на цьому відрізку
і всюди на цьому відрізку  , то
, то .
. , якщо
, якщо  .
. , то
, то .
. також інтегровна на цьому відрізку, причому
також інтегровна на цьому відрізку, причому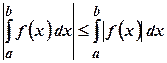 .
. і
і  - відповідно її найменше і найбільше значення на цьому відрізку, то справджуються нерівності
- відповідно її найменше і найбільше значення на цьому відрізку, то справджуються нерівності .
. така, що виконується рівність:
така, що виконується рівність: .
. , де функція
, де функція  та інтегровною на ньому,
та інтегровною на ньому,  .
. для усіх
для усіх  .
. ,
, - яка-небудь її первісна.
- яка-небудь її первісна. .
. . Обчислимо її значення при верхній границі
. Обчислимо її значення при верхній границі  , при нижній границі
, при нижній границі  . За формулою Ньютона-Лейбніца значення інтегралу становить
. За формулою Ньютона-Лейбніца значення інтегралу становить 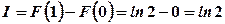 .
. .
.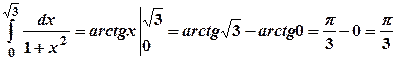 .
.
 .
.
 .
.
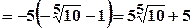 .
. .
. . Отримаємо:
. Отримаємо:
 .
. .
.

 .
. .
. представимо у вигляді суми найпростіших дробів, а саме
представимо у вигляді суми найпростіших дробів, а саме .
. .
.
 .
.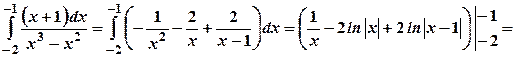

 .
. ;
; ;
; ;
; ;
; ;
; ;
;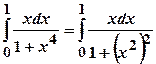 .
. . Тоді
. Тоді  ,
, 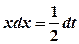 .
. , то
, то 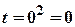 , при
, при 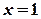
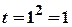 .
. .
.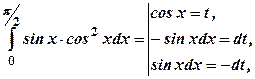

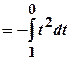 .
. .
.

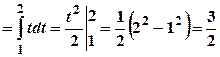 .
.
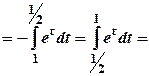
 .
.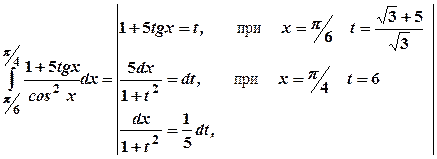 =
=
 .
.


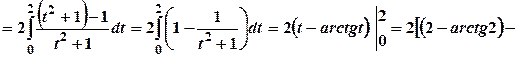
 .
. .
. , зробимо заміну
, зробимо заміну 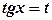 .
.
 =
=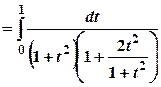 =
= 

 .
. .
. :
: 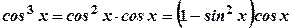 .
.








 .
.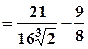 .
. .
.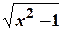 . Зробимо заміну
. Зробимо заміну  ,
,  . Тоді
. Тоді  . Щоб знайти нові межі інтегрування, виразимо
. Щоб знайти нові межі інтегрування, виразимо  через
через  .
.
 ,
,
 .
. 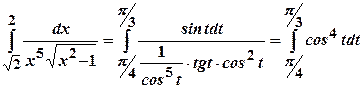 .
.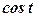 , скористуємось двічі формулою пониження степеня:
, скористуємось двічі формулою пониження степеня:

 .
.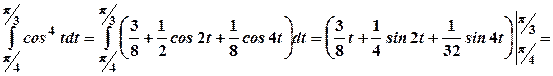

 .
. .
. . Тоді
. Тоді 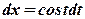 ,
,  .
.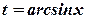 , тому при
, тому при 
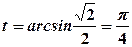 ,
, .
.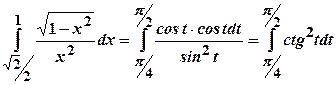 .
. , звідки
, звідки  ,
,  .
.
 , при
, при 
 .
.
 .
. ;
; ;
; ;
; ;
;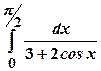 ;
; ;
; .
. .
.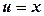 ,
,  ; тоді
; тоді  ,
,  . Отримаємо:
. Отримаємо:
 .
.

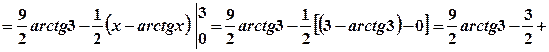
 .
.


 .
.

 .
. .
.

 .
. . Тоді
. Тоді , звідки
, звідки  ,
,  .
. .
. .
.
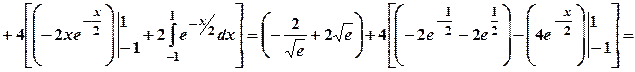

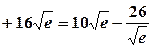 .
. ;
; ;
; ;
;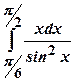 ;
; .
.
 кв. од.
кв. од. .
.


 кв. од.
кв. од. .
. і прямою
і прямою  .
. Щоб визначити межі інтегрування, знайдемо абсциси точок перетину ліній
Щоб визначити межі інтегрування, знайдемо абсциси точок перетину ліній  , звідки
, звідки  .
. , тому обчислимо площу її правої половини, а загальний результат подвоємо.
, тому обчислимо площу її правої половини, а загальний результат подвоємо. кв. од.
кв. од. .
. Фігура на відрізку
Фігура на відрізку  обмежена зверху
обмежена зверху  , знизу прямою
, знизу прямою  . Її площу знайдемо за формулою (3.3):
. Її площу знайдемо за формулою (3.3): кв. од.
кв. од. .
. . Приведемо рівняння до канонічного виду, виділивши повний квадрат:
. Приведемо рівняння до канонічного виду, виділивши повний квадрат: .
. і перетинає вісь
і перетинає вісь  в точках
в точках  .
. На відрізку
На відрізку  функція
функція 


 кв. од.
кв. од. .
. :
: тоді
тоді  .
. .
. Точки перетину з віссю
Точки перетину з віссю  , тоді
, тоді , звідки
, звідки ,
,  .
.


 кв. од.
кв. од. .
. Для знаходження абсцис точок перетину графіків розв’яжемо систему рівнянь:
Для знаходження абсцис точок перетину графіків розв’яжемо систему рівнянь: , тоді
, тоді  ,
,  ,
,  , звідки
, звідки  .
.

 кв. од.
кв. од.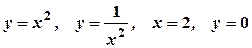 .
. Точки перетину графіків:
Точки перетину графіків: , тоді
, тоді  ,
,  , звідки
, звідки  .
. . На відрізку
. На відрізку  фігура зверху обмежена спочатку графіком функції
фігура зверху обмежена спочатку графіком функції  ), а потім графіком
), а потім графіком  (якщо
(якщо  ). Тому площу всієї фігури знайдемо як суму двох площ, кожну з яких обчислимо за формулою (3.1).
). Тому площу всієї фігури знайдемо як суму двох площ, кожну з яких обчислимо за формулою (3.1). ,
, кв. од.,
кв. од.,  кв. од.
кв. од. кв. од.
кв. од. та однією аркою циклоїди
та однією аркою циклоїди .
.
 до
до  . Використавши формулу (3.5), маємо:
. Використавши формулу (3.5), маємо:


 кв. од.
кв. од. ,
, .
. Крива симетрична відносно осі
Крива симетрична відносно осі  та
та  відповідають значення параметрів
відповідають значення параметрів  .
. :
:  .
.



 .
. кв. од.
кв. од. .
.
 , коли радіус-вектор точки на лемніскаті описує чверть шуканої площі.
, коли радіус-вектор точки на лемніскаті описує чверть шуканої площі. ,
,  . Визна-чимо, чому дорівнює кут
. Визна-чимо, чому дорівнює кут  в рівняння кривої, отримаємо:
в рівняння кривої, отримаємо:  ,
,  ,
,  , звідки
, звідки  .
. . Тоді за формулою (3.6):
. Тоді за формулою (3.6): .
. кв. од.
кв. од. .
. (або
(або  ), де
), де  - постійні величини, називаються розами. Якщо
- постійні величини, називаються розами. Якщо  - пелюсток, якщо
- пелюсток, якщо  , звідки
, звідки  .
.


