
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 6. Інтегральне числення функцій багатьох зміннихСодержание книги Поиск на нашем сайте
Розділ 6. Інтегральне числення функцій багатьох змінних Об'єм циліндричного тіла Розглянемо в просторі тіло
Рис. 6.1.
Для розв'язання поставленої задачі розіб'ємо довільно область Для визначення об'єму
Виконуючи обчислення для кожної області ділення і додаючи результати, одержуємо наближене значення об'єму даного циліндричного тіла
Отже, отримали об'єм східчастого тіла з основою S, “покритого” зверху частинами площин, рівняння яких
Точне значення об'єму циліндричного тіла дорівнює границі, до якої прямує знайдене наближене значення об'єму при необмеженому зменшенні областей ділення, тобто
Означення подвійного інтеграла Нехай задана функція
Таким чином:
Функція Геометричний зміст подвійного інтеграла можна пояснити, скориставшись результатом розв'язку розглянутої задачі (рис. 6.1). Для невід’ємної неперервної в області Якщо ж підінтегральна функція Якщо ж неперервна функція
Рис. 6.2. Зазначені поняття використовуються при обчисленні об'ємів тіл за допомогою подвійних інтегралів.
Застосування подвійного інтеграла в геометрії Площа плоскої фігури. На підставі властивостей подвійного інтеграла Для Отже, у прямокутних координатах
У полярній системі координат
Приклад 6.4. Обчислити площу фігури, що обмежена лініями Розв’язання. Розглянемо область Отже, Тоді
Приклад 6.5. Обчислити площу фігури, що обмежена лініями Розв’язання. Перетворимо перші два рівняння до канонічного вигляду, одержимо
Як видно з рисунка, дану площу не можна обчислити за допомогою одного подвійного інтеграла в прямокутних координатах. В полярній системі координат область є простою по Очевидно, що Тоді
Об'єм тіла. Виходячи з геометричного змісту подвійного інтеграла, об'єм тіла з основою
Приклад 6.6. Знайти об'єм тіла Розв’язання. Дане тіло є циліндричним з основою В силу симетричності тіла відносно координатної площини
Оскільки
Приклад 6.7. Обчислити об'єм тіла, обмеженого поверхнями
Розв’язання. Оскільки основою тіла в площині де Тоді Отже
Площа поверхні. Розглянемо поверхню, задану рівнянням
Маса плоскої пластини. Розглянемо тонку пластину, розташовану в площині, яка займає область Поверхневою щільністю такої пластинки в даній точці називається границя відношення маси
Якщо Нехай пластинка неоднорідна, тобто Розіб'ємо область Тоді масу кожної елементарної ділянки можна вважати приблизно рівною
Масу всієї пластинки
Точний результат знайдемо, перейшовши в останній рівності до границі:
Формулу (6.12) можна розглядати як механічний зміст подвійного інтеграла: подвійний інтеграл
Статичні моменти. Аналогічно міркуючи, можна одержати формули для обчислення статичних моментів пластинки
Координати центра мас. У механіці доводиться, що статичний момент пластинки відносно якої-небудь осі збігається зі статичним моментом точкової маси, рівної масі пластинки, зосередженої в центрі ваги її відносно тієї ж осі. Звідси, позначаючи через
Отже,
Моменти інерції. Аналогічно, для моментів інерції пластинки одержуємо:
Можна показати, що полярний момент пластинки обчислюється за формулою
Очевидно, що
Приклад 6.8. Обчислити координати центра ваги півкола, щільність розподілу маси якого пропорційна квадрату відстані точки від діаметра цього півкола.
Розв’язання. Нехай вісь
Вправи 6.1. Побудувати області, площі яких виражаються інтегралами: 1) Змінити порядок інтегрування й обчислити площі. 6.2. Змінити порядок інтегрування: а) б) в) 6.3. Представити подвійний інтеграл а) б) в) 6.4. Обчислити 6.5. Обчислити 6.6. Обчислити інтеграли: а) б) в) г) д) 6.7. Знайти об’єм тіла, обмеженого поверхнями (за допомогою подвійного інтегралу): а) б) в) 6.8. Знайти площу області, яка обмежена кривими: а) 6.9. Знайти об'єм тіла, обмеженого еліптичним параболоїдом 6.10. Обчислити об'єм тіла, обмеженого площиною 6.11. Обчислити координати центра ваги фігури, обмеженої кривими: а) б) в) г) 6.12. Обчислити: а) б) в) г) д) 6.13. Обчислити 6.14. Знайти об’єм тіла, обмеженого поверхнями: а) б) в) 6.15. Визначити центр мас однорідного тіла, обмеженого поверхнею 6.16. Знайти масу тіла, обмеженого поверхнями: а) б) в)
Розділ 7. Ряди Властивості числових рядів Розглянемо деякі властивості числових рядів. Властивість 1. Якщо ряд Дійсно, якщо ряд Очевидно, що якщо ряд Виходить, поведінка ряду не зміниться, якщо всі його члени помножити на однакове число. Властивість 2. Якщо ряди Справді нехай Враховуючи, що Таким чином, ряди, що є збіжними, можна почленно додавати, при цьому одержуємо ряд, що є збіжним. Різниця двох рядів, що є збіжними, також ряд, що є збіжним. Очевидно, що сума збіжного і розбіжного ряду – розбіжний ряд. Загального висновку щодо алгебраїчної суми розбіжних рядів зробити не можна. В одних випадках у результаті можемо одержати розбіжний ряд, в інших – збіжний. Властивість 3. Збіжність і розбіжність ряду не порушиться, якщо відкинути чи додати скінченне число членів ряду. Властивість випливає з означення збіжного ряду. З цієї властивості випливає, що ряд
Ознака порівняння. Знакопостійним рядом будемо називати ряд, члени якого мають однаковий знак. До знакопостійних рядів відносять знакододатні та знаковід’ємні ряди. Будемо далі розглядати знакододатні ряди, оскільки дослідження знаковід’ємних рядів можна звести до дослідження знакододатніх рядів винесенням за дужки числа Нехай дано два ряди з невід’ємними членами:
Відомо, що Якщо ряд з більшими членами Якщо ряд з меншими членами Дійсно, нехай Якщо ряд Але оскільки Якщо ж ряд Приклад 7.4. Дослідити збіжність рядів: а) Розв’язання. У випадку а): порівняємо даний ряд з рядом У випадку б): порівняємо даний ряд з гармонічним рядом
Ознака Даламбера. Нехай для знакододатнього ряду У такому випадку, якщо ця границя Нехай є знакододатній ряд
Тоді, починаючи з деякого номера члена буде виконуватися нерівність
де
Нехай Тоді
Додавши нерівності, одержимо:
Але оскільки число Нехай тепер Якщо ж Приклад 7.6. Дослідити на збіжність ряди: а) Розв’язання. У випадку а): У випадку б): і У випадку в):
Радикальна ознака Коші. Якщо для ряду Нехай
Додаючи нерівності маємо:
У правій частині нерівності – геометричний ряд, що є збіжним. На підставі ознаки порівняння ряд
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 634; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |

 , обмежене зверху поверхнею, заданою рівнянням
, обмежене зверху поверхнею, заданою рівнянням  , збоку – циліндричною поверхнею з твірними, паралельними вісі
, збоку – циліндричною поверхнею з твірними, паралельними вісі 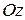 , знизу областю
, знизу областю  площини
площини  (
(
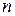 частин:
частин:  ,
,  ,...,
,...,  і розглянемо циліндричне тіло як сукупність циліндричних стовпчиків з основами
і розглянемо циліндричне тіло як сукупність циліндричних стовпчиків з основами  кожного циліндричного стовпчика візьмемо в області
кожного циліндричного стовпчика візьмемо в області  довільну точку
довільну точку  і побудуємо циліндр із основою
і побудуємо циліндр із основою  . Такий циліндр обмежений зверху частиною поверхні, рівняння якої
. Такий циліндр обмежений зверху частиною поверхні, рівняння якої 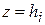 . Об'єм цього циліндра
. Об'єм цього циліндра  можна прийняти за наближене значення об'єму циліндричного стовпчика
можна прийняти за наближене значення об'єму циліндричного стовпчика  .
. .
. .
. .
. . Обчислимо значення функції в обраних точках
. Обчислимо значення функції в обраних точках  . Складемо добуток
. Складемо добуток  для кожного розбиття. Додамо всі добутки, одержимо суму
для кожного розбиття. Додамо всі добутки, одержимо суму  , яка буде інтегральною сумою для функції
, яка буде інтегральною сумою для функції  в області
в області  або
або  .
. . (6.2)
. (6.2) недодатня неперервна в замкнутій області
недодатня неперервна в замкнутій області  і від'ємною в області
і від'ємною в області  (рис. 6.2), то подвійний інтеграл
(рис. 6.2), то подвійний інтеграл 
 .
. підінтегральна функція
підінтегральна функція  і виходячи з геометричного змісту подвійного інтеграла одержимо об'єм циліндричного тіла висотою
і виходячи з геометричного змісту подвійного інтеграла одержимо об'єм циліндричного тіла висотою  , що дорівнює площі основи тіла, тобто
, що дорівнює площі основи тіла, тобто  . (6.9)
. (6.9) , тому
, тому . (6.10)
. (6.10) Рис. 6.11.
Рис. 6.11.
 ,
,  (рис. 6.11).
(рис. 6.11).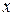 і запишемо її нерівностями. Для цього знайдемо точки перетину ліній, що обмежують область (крайні точки області по вісі
і запишемо її нерівностями. Для цього знайдемо точки перетину ліній, що обмежують область (крайні точки області по вісі  ), розв’язавши систему рівнянь
), розв’язавши систему рівнянь 


 ,
,  ,
,  ,
,  .
. ,
,  . Перше рівняння визначає коло з центром у точці (1;0) з радіусом
. Перше рівняння визначає коло з центром у точці (1;0) з радіусом  , друге рівняння також визначає коло з центром у точці (2;0) з радіусом
, друге рівняння також визначає коло з центром у точці (2;0) з радіусом 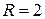 (рис. 6.12).
(рис. 6.12). Рис. 6.12.
Рис. 6.12.
 . Рівняння кіл, що обмежують область у полярній системі координат, одержимо, підставивши в їхні початкові рівняння
. Рівняння кіл, що обмежують область у полярній системі координат, одержимо, підставивши в їхні початкові рівняння  ,
,  . Тоді рівняння першого кола набуде вигляду
. Тоді рівняння першого кола набуде вигляду  , а для другого відповідно
, а для другого відповідно  .
.

 (кв. од.)
(кв. од.) . (6.10)
. (6.10) , обмеженого поверхнями
, обмеженого поверхнями  ,
,  ,
,  ,
,  (рис. 6.13).
(рис. 6.13). .
. можна обчислити об'єм тіла з основою
можна обчислити об'єм тіла з основою 




 ,
,  , z=0 (рис. 6.15).
, z=0 (рис. 6.15). Рис. 6.15.
Рис. 6.15.
 , обчислимо об'єм, використовуючи полярну систему координат. Зверху тіло обмежене поверхнею
, обчислимо об'єм, використовуючи полярну систему координат. Зверху тіло обмежене поверхнею  . Тому
. Тому  ,
, . Область
. Область 
 .
. . (6.11)
. (6.11) елементарної ділянки, що містить цю точку, до її площі
елементарної ділянки, що містить цю точку, до її площі  за умови, що площа ділянки стягується до даної точки. Позначимо щільність
за умови, що площа ділянки стягується до даної точки. Позначимо щільність  , маємо
, маємо .
. стала в кожній точці області, то маса обчислюється за формулою
стала в кожній точці області, то маса обчислюється за формулою  , де
, де  – площа пластинки.
– площа пластинки. .
. .
. .
. .
. . (6.12)
. (6.12) .
. ;
;  . (6.13)
. (6.13) координати центра мас пластинки
координати центра мас пластинки  ;
;  .
. ,
,  , (6.14)
, (6.14) ;
;  . (6.15)
. (6.15) . (6.16)
. (6.16) .
. Рис. 6.16.
Рис. 6.16.
 перпендикулярна до вісі
перпендикулярна до вісі  (рис. 6.16). При такому виборі осей координат щільність
(рис. 6.16). При такому виборі осей координат щільність 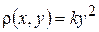 (
( – коефіцієнт пропорційності),
– коефіцієнт пропорційності),  ,
,  , де
, де  ,
, ,
, .
. ; 2)
; 2)  .
. ;
; ;
; .
. за допомогою повторних із зовнішнім інтегруванням по
за допомогою повторних із зовнішнім інтегруванням по  :
: :
:  ,
,  ,
,  ;
; ,
,  ;
; ,
, 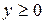 .
. , де
, де  – криволінійний трикутник, обмежений параболою
– криволінійний трикутник, обмежений параболою  і прямими
і прямими  ,
,  , де
, де  ,
,  ;
; ;
; ,
,  ,
,  ,
,  ;
; ; є)
; є)  .
. ,
,  ,
,  ;
; ,
,  ,
,  ,
,  ,
,  ,
,  ; б)
; б)  ; в)
; в)  .
. , площиною
, площиною  і конусом
і конусом  .
. ,
,  ;
; ,
,  ;
; ,
,  ,
,  ,
,  ;
; ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , де
, де  .
. ,
,  ,
,  ,
,  ,
,  і координатними площинами.
і координатними площинами. ,
,  ;
; ,
,  ,
,  ;
; ,
,  ,
,  .
.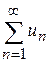 є збіжним і його сума
є збіжним і його сума  , де
, де  , також є збіжним і його сума
, також є збіжним і його сума  .
. , і, отже
, і, отже  , але
, але  – частинні суми ряду
– частинні суми ряду  .
. є розбіжним, то і ряд
є розбіжним, то і ряд  , також є розбіжним.
, також є розбіжним. є збіжними і їхні суми відповідно рівні
є збіжними і їхні суми відповідно рівні  , то і ряд
, то і ряд  є збіжним і його сума дорівнює
є збіжним і його сума дорівнює  .
. і
і  , – частинні суми відповідних рядів, тоді за умовою
, – частинні суми відповідних рядів, тоді за умовою 
 , звідси
, звідси  .
. частинні суми ряду
частинні суми ряду  .
. поводяться однаково, обидва є збіжними або обидва є розбіжними.
поводяться однаково, обидва є збіжними або обидва є розбіжними. .
. ;
; .
.
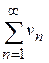 є збіжним, то ряд з меншими членами
є збіжним, то ряд з меншими членами  і його частинні суми обмежені, тобто при всіх
і його частинні суми обмежені, тобто при всіх  , де
, де  – деяке число.
– деяке число. , то частинні суми ряду
, то частинні суми ряду  ; б)
; б)  .
. , що є геометричним зі знаменником
, що є геометричним зі знаменником  , тобто збігається. Оскільки
, тобто збігається. Оскільки  для всіх
для всіх 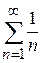 , що є розбіжним. Оскільки
, що є розбіжним. Оскільки  , то досліджуваний ряд також є розбіжним.
, то досліджуваний ряд також є розбіжним. і дорівнює скінченному числу
і дорівнює скінченному числу 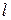 :
:  .
.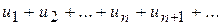 і нехай
і нехай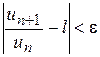 ,
,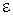 – як завгодно мале наперед задане додатнє число. Звідси для всіх номерів
– як завгодно мале наперед задане додатнє число. Звідси для всіх номерів  буде виконуватися нерівність
буде виконуватися нерівність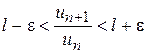 .
.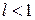 . Тоді можна взяти число
. Тоді можна взяти число  також буде меншим від одиниці. Нехай
також буде меншим від одиниці. Нехай 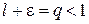 .
.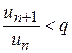 або
або  для всіх
для всіх  ,
, 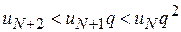 ,
, 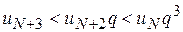 ,...
,... .
. , то у правій частині нерівності маємо геометричний ряд, що збігається. Тоді за ознакою порівняння ряд в лівій частині нерівності також збіжний. Отже на підставі властивості 3 числових рядів заданий ряд
, то у правій частині нерівності маємо геометричний ряд, що збігається. Тоді за ознакою порівняння ряд в лівій частині нерівності також збіжний. Отже на підставі властивості 3 числових рядів заданий ряд 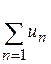 також збіжний.
також збіжний.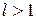 , тобто
, тобто 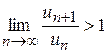 . Але тоді
. Але тоді  , що свідчить про те, що члени ряду
, що свідчить про те, що члени ряду 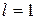 , можна показати, що ознака однозначної відповіді не дає. В одних випадках ряд є збіжним, в інших – розбіжний. Для дослідження ряду потрібно застосовувати яку-небудь іншу ознаку збіжності.
, можна показати, що ознака однозначної відповіді не дає. В одних випадках ряд є збіжним, в інших – розбіжний. Для дослідження ряду потрібно застосовувати яку-небудь іншу ознаку збіжності.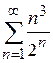 ; б)
; б)  ; в)
; в) 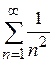 .
.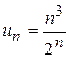 ,
, 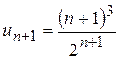 і
і 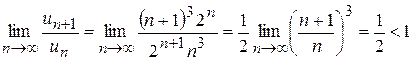 . Отже ряд збіжний.
. Отже ряд збіжний.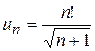 ,
, 
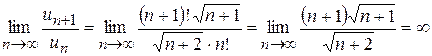 . Ряд розбіжний.
. Ряд розбіжний. ,
,  і
і  . Ознака Даламбера відповіді не дає.
. Ознака Даламбера відповіді не дає. , то при
, то при  ряд збіжний, при
ряд збіжний, при 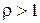 ряд розбіжний, при
ряд розбіжний, при 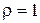 ознака відповіді не дає.
ознака відповіді не дає. , що задовольняє умові
, що задовольняє умові 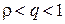 . Тоді знайдеться такий номер члена послідовності
. Тоді знайдеться такий номер члена послідовності  , починаючи з якого виконується нерівність
, починаючи з якого виконується нерівність 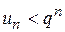 . Підставляючи значення
. Підставляючи значення  ,..., одержуємо:
,..., одержуємо: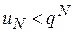 ;
; 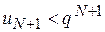 ;
; 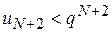 ;....
;.... .
.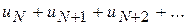 збіжний, а значить і ряд
збіжний, а значить і ряд 


