
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ознака порівняння в граничній формі.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Якщо для рядів
то ряди поводять себе однаково: або обидва є збіжними, або обидва є розбіжними. Нехай існує скінченна границя Тоді, якщо ряд Якщо ряд Приклад 7.5. Дослідити на збіжність ряд Розв’язання. Порівняємо ряд з рядом Тут
Ознака Даламбера. Нехай для знакододатнього ряду У такому випадку, якщо ця границя Нехай є знакододатній ряд
Тоді, починаючи з деякого номера члена буде виконуватися нерівність
де
Нехай Тоді
Додавши нерівності, одержимо:
Але оскільки число Нехай тепер Якщо ж Приклад 7.6. Дослідити на збіжність ряди: а) Розв’язання. У випадку а): У випадку б): і У випадку в):
Радикальна ознака Коші. Якщо для ряду Нехай
Додаючи нерівності маємо:
У правій частині нерівності – геометричний ряд, що є збіжним. На підставі ознаки порівняння ряд Приклад 7.7. Дослідити на збіжність ряд Розв’язання. Тут
Інтегральна ознака Коші. Якщо для знакододатнього ряду Доведення проведемо на підставі геометричного змісту визначеного інтеграла. Зобразимо графічно Дано
Рис. 7.1.
Обчислюючи площу криволінійної трапеції наближено з недостачею як суму площ прямокутників з основою, рівною одиниці і висотою, рівною значенню функції в правому кінці основи, одержимо
Якщо ж обчислити площу криволінійної трапеції наближено з надлишком як суму площ прямокутників, з основою, рівною одиниці і висотою, рівною значенню функції в лівому кінці основи, одержимо
тобто
Звідси:
Нехай інтеграл Оскільки Нехай тепер З нерівності (7.8) випливає, що Дослідимо дуже важливий за своїм застосуванням узагальнений гармонічний ряд (ряд Діріхле), що має вигляд
де Дослідимо ряд за допомогою інтегральної ознаки збіжності. Тут Для
При При При Отже, ряд Діріхле
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.01 с.) |

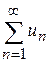 і
і 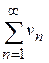 виконується необхідна ознака збіжності і
виконується необхідна ознака збіжності і ,
,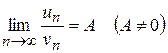 . За означенням границі
. За означенням границі  або
або  . Звідки
. Звідки  . Тому
. Тому  .
. , а отже збіжний і ряд
, а отже збіжний і ряд 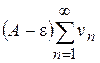 також розбіжний, а отже, розбіжний і ряд
також розбіжний, а отже, розбіжний і ряд 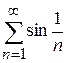 .
.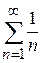 , застосувавши ознаку порівняння в граничній формі.
, застосувавши ознаку порівняння в граничній формі.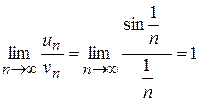 (на підставі першої істотної границі). Отже, ряди поводять себе однаково і ряд
(на підставі першої істотної границі). Отже, ряди поводять себе однаково і ряд  і дорівнює скінченному числу
і дорівнює скінченному числу 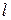 :
:  .
.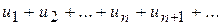 і нехай
і нехай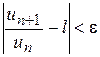 ,
,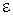 – як завгодно мале наперед задане додатнє число. Звідси для всіх номерів
– як завгодно мале наперед задане додатнє число. Звідси для всіх номерів  буде виконуватися нерівність
буде виконуватися нерівність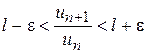 .
.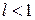 . Тоді можна взяти число
. Тоді можна взяти число  також буде меншим від одиниці. Нехай
також буде меншим від одиниці. Нехай 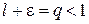 .
.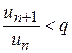 або
або  для всіх
для всіх  ,
, 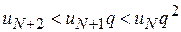 ,
, 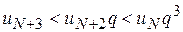 ,...
,... .
. , то у правій частині нерівності маємо геометричний ряд, що збігається. Тоді за ознакою порівняння ряд в лівій частині нерівності також збіжний. Отже на підставі властивості 3 числових рядів заданий ряд
, то у правій частині нерівності маємо геометричний ряд, що збігається. Тоді за ознакою порівняння ряд в лівій частині нерівності також збіжний. Отже на підставі властивості 3 числових рядів заданий ряд 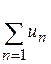 також збіжний.
також збіжний.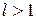 , тобто
, тобто 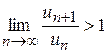 . Але тоді
. Але тоді  , що свідчить про те, що члени ряду
, що свідчить про те, що члени ряду 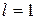 , можна показати, що ознака однозначної відповіді не дає. В одних випадках ряд є збіжним, в інших – розбіжний. Для дослідження ряду потрібно застосовувати яку-небудь іншу ознаку збіжності.
, можна показати, що ознака однозначної відповіді не дає. В одних випадках ряд є збіжним, в інших – розбіжний. Для дослідження ряду потрібно застосовувати яку-небудь іншу ознаку збіжності.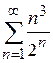 ; б)
; б)  ; в)
; в) 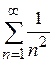 .
.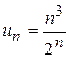 ,
, 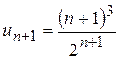 і
і 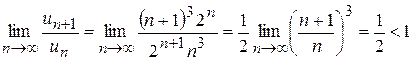 . Отже ряд збіжний.
. Отже ряд збіжний.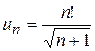 ,
, 
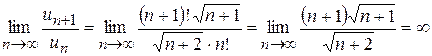 . Ряд розбіжний.
. Ряд розбіжний. ,
,  і
і  . Ознака Даламбера відповіді не дає.
. Ознака Даламбера відповіді не дає. , то при
, то при  ряд збіжний, при
ряд збіжний, при 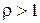 ряд розбіжний, при
ряд розбіжний, при 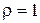 ознака відповіді не дає.
ознака відповіді не дає. , що задовольняє умові
, що задовольняє умові 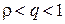 . Тоді знайдеться такий номер члена послідовності
. Тоді знайдеться такий номер члена послідовності  , починаючи з якого виконується нерівність
, починаючи з якого виконується нерівність 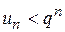 . Підставляючи значення
. Підставляючи значення  ,..., одержуємо:
,..., одержуємо: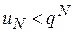 ;
; 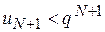 ;
; 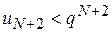 ;....
;.... .
.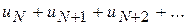 збіжний, а значить і ряд
збіжний, а значить і ряд 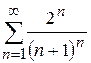 .
.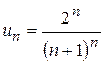 ,
, 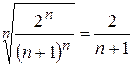 і
і 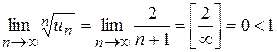 . Отже ряд збіжний.
. Отже ряд збіжний.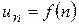 така, що відповідна їй функція
така, що відповідна їй функція 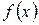 неперервного аргументу
неперервного аргументу 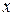 невід’ємна, неперервна, яка монотонно спадає на півінтервалі
невід’ємна, неперервна, яка монотонно спадає на півінтервалі  , то невласний інтеграл
, то невласний інтеграл  і ряд
і ряд  – площу криволінійної трапеції, обмеженої зверху графіком функції
– площу криволінійної трапеції, обмеженої зверху графіком функції  , знизу – проміжком
, знизу – проміжком 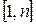 на вісі абсцис (рис. 7.1).
на вісі абсцис (рис. 7.1).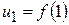 ,
, 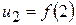 ,
, 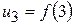 ,...,
,..., 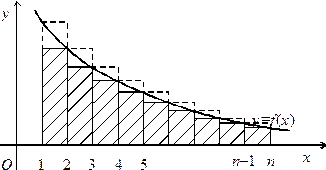
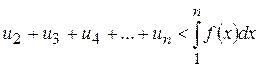 .
.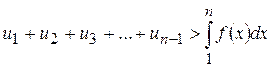 ,
,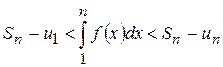 .
. ; (7.7)
; (7.7)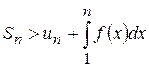 . (7.8)
. (7.8)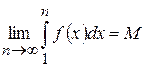 .
.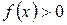 , то послідовність
, то послідовність 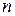 і обмежена зверху своєю границею:
і обмежена зверху своєю границею: 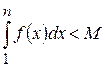 . З нерівності (7.7) випливає, що
. З нерівності (7.7) випливає, що 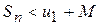 , тобто послідовність частинних сум обмежена зверху, а значить має скінченну границю, ряд є збіжним.
, тобто послідовність частинних сум обмежена зверху, а значить має скінченну границю, ряд є збіжним. при
при  при
при 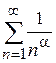 ,
,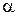 – будь-яке додатнє число (при
– будь-яке додатнє число (при 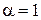 маємо простий гармонічний ряд).
маємо простий гармонічний ряд).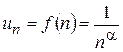 , що відповідає функції неперервного аргументу
, що відповідає функції неперервного аргументу  .
.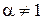 невласний інтеграл має вигляд
невласний інтеграл має вигляд .
.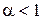 маємо
маємо  .
.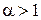 –
– 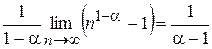 .
. .
.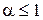 . Зокрема, ряд
. Зокрема, ряд 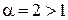 , чого не можна було встановити за допомогою ознаки Даламбера.
, чого не можна було встановити за допомогою ознаки Даламбера.


