
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числові ряди. Основні поняттяСодержание книги Поиск на нашем сайте
Розглянемо числову послідовність Означення 7.1. Рядом називається нескінченна сума числової послідовності
де Елемент Наприклад, якщо Для Суму перших
Частинні суми ряду утворюють послідовність Означення 7.2. Числовий ряд (7.1) називається збіжним, якщо для нього існує скінченна границя послідовності частинних сум, тобто
При цьому, скінченне число
Якщо Таким чином, щоб встановити, чи є збіжним чи розбіжним даний числовий ряд, потрібно знайти його суму як границю послідовності частинних сум при Означення 7.3. Залишком ряду (7.1) називається
тобто Приклад 7.1. Дослідити на збіжність числовий ряд
Розв’язання. Знайдемо для даного ряду
Тоді Отже, даний ряд є збіжним. Зазначимо, що основною задачею теорії рядів є дослідження збіжності. Геометричним рядом називають числовий ряд
члени якого утворюють нескінченну геометричну прогресію зі знаменником Приклад 7.2. Дослідити на збіжність геометричний ряд. Розв’язання. Як відомо, сума перших
Тоді Оскільки
Отже, геометричний ряд є збіжним при Для випадку
Отже, для цього випадку
Властивості числових рядів Розглянемо деякі властивості числових рядів. Властивість 1. Якщо ряд Дійсно, якщо ряд Очевидно, що якщо ряд Виходить, поведінка ряду не зміниться, якщо всі його члени помножити на однакове число. Властивість 2. Якщо ряди Справді нехай Враховуючи, що Таким чином, ряди, що є збіжними, можна почленно додавати, при цьому одержуємо ряд, що є збіжним. Різниця двох рядів, що є збіжними, також ряд, що є збіжним. Очевидно, що сума збіжного і розбіжного ряду – розбіжний ряд. Загального висновку щодо алгебраїчної суми розбіжних рядів зробити не можна. В одних випадках у результаті можемо одержати розбіжний ряд, в інших – збіжний. Властивість 3. Збіжність і розбіжність ряду не порушиться, якщо відкинути чи додати скінченне число членів ряду. Властивість випливає з означення збіжного ряду. З цієї властивості випливає, що ряд
Необхідна ознака збіжності ряду Теорема 7.1. Якщо ряд Дійсно, якщо ряд є збіжним, його частинні суми при Представимо загальний член ряду у вигляді Зазначимо, що умова Прикладом такого ряду є гармонічний ряд Для цього ряду Приймаючи
Додаючи нерівності, маємо Тоді Приклад 7.3. Перевірити необхідну ознаку збіжності для рядів: а) Розв’язання. Для випадку а): Для випадку б): Отже, необхідна ознака збіжності стверджує, що всі ряди, що є збіжними, знаходяться серед тих рядів, у яких
Достатні ознаки збіжності знакопостійних рядів Ознака порівняння. Знакопостійним рядом будемо називати ряд, члени якого мають однаковий знак. До знакопостійних рядів відносять знакододатні та знаковід’ємні ряди. Будемо далі розглядати знакододатні ряди, оскільки дослідження знаковід’ємних рядів можна звести до дослідження знакододатніх рядів винесенням за дужки числа Нехай дано два ряди з невід’ємними членами:
Відомо, що Якщо ряд з більшими членами Якщо ряд з меншими членами Дійсно, нехай Якщо ряд Але оскільки Якщо ж ряд Приклад 7.4. Дослідити збіжність рядів: а) Розв’язання. У випадку а): порівняємо даний ряд з рядом У випадку б): порівняємо даний ряд з гармонічним рядом
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.9.169 (0.009 с.) |

 ,
, 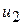 ,...,
,...,  ,...
,... (7.1)
(7.1) , маємо ряд
, маємо ряд  .
. одержуємо ряд
одержуємо ряд  .
.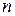 членів ряду називають
членів ряду називають 

 ….
…. , яка при
, яка при  може мати або не мати границю.
може мати або не мати границю. (7.2)
(7.2) називають сумою ряду, тобто для ряду, що є збіжним,
називають сумою ряду, тобто для ряду, що є збіжним, . (7.3)
. (7.3) або не існує, то ряд називається розбіжним.
або не існує, то ряд називається розбіжним. .
. (7.4)
(7.4) .
. .
. . Оскільки
. Оскільки  , то можна записати ряд у вигляді
, то можна записати ряд у вигляді .
. і
і  .
.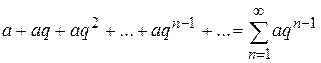 , (7.5)
, (7.5) .
. членів геометричної прогресії дорівнює
членів геометричної прогресії дорівнює . (7.6)
. (7.6) .
. одержимо, що
одержимо, що
 , його сума при цьому виражається числом
, його сума при цьому виражається числом  , і є розбіжним, при
, і є розбіжним, при  .
. одержуємо ряд
одержуємо ряд  , сума перших
, сума перших  , отже
, отже  і ряд є розбіжним. Для випадку
і ряд є розбіжним. Для випадку  одержуємо ряд
одержуємо ряд  , для якого
, для якого

 не існує і ряд є розбіжним.
не існує і ряд є розбіжним.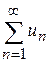 є збіжним і його сума
є збіжним і його сума  , де
, де  , також є збіжним і його сума
, також є збіжним і його сума  .
. , і, отже
, і, отже  , але
, але  – частинні суми ряду
– частинні суми ряду  .
. є розбіжним, то і ряд
є розбіжним, то і ряд  , також є розбіжним.
, також є розбіжним. є збіжними і їхні суми відповідно рівні
є збіжними і їхні суми відповідно рівні  , то і ряд
, то і ряд  є збіжним і його сума дорівнює
є збіжним і його сума дорівнює  .
. , – частинні суми відповідних рядів, тоді за умовою
, – частинні суми відповідних рядів, тоді за умовою 
 , звідси
, звідси  .
. частинні суми ряду
частинні суми ряду  .
. поводяться однаково, обидва є збіжними або обидва є розбіжними.
поводяться однаково, обидва є збіжними або обидва є розбіжними.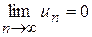 .
. . Тоді
. Тоді  . Очевидно, що якщо
. Очевидно, що якщо  ряд є розбіжним.
ряд є розбіжним. .
.
 . Обчислимо суму цього ряду так. Відомо, що
. Обчислимо суму цього ряду так. Відомо, що  . Причому,
. Причому,  . Прологарифмуємо цю нерівність,
. Прологарифмуємо цю нерівність,  ,
, 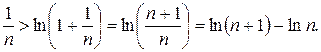
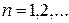 одержимо, що
одержимо, що
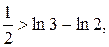

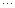

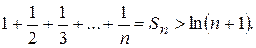
 , тобто гармонічний ряд є розбіжним.
, тобто гармонічний ряд є розбіжним.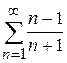 ; б)
; б)  .
. ознака не виконується, отже, ряд є розбіжним.
ознака не виконується, отже, ряд є розбіжним. Ознака виконується, але нічого про збіжність ряду сказати не можна. Ряд може бути збіжним і може бути і розбіжним.
Ознака виконується, але нічого про збіжність ряду сказати не можна. Ряд може бути збіжним і може бути і розбіжним. Але в цій групі рядів є і розбіжні.
Але в цій групі рядів є і розбіжні. .
. ;
; .
.
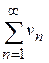 є збіжним, то ряд з меншими членами
є збіжним, то ряд з меншими членами  і його частинні суми обмежені, тобто при всіх
і його частинні суми обмежені, тобто при всіх  , де
, де  – деяке число.
– деяке число. , то частинні суми ряду
, то частинні суми ряду  ; б)
; б)  .
. , що є геометричним зі знаменником
, що є геометричним зі знаменником  , тобто збігається. Оскільки
, тобто збігається. Оскільки  для всіх
для всіх 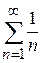 , що є розбіжним. Оскільки
, що є розбіжним. Оскільки  , то досліджуваний ряд також є розбіжним.
, то досліджуваний ряд також є розбіжним.


