
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Область збіжності степеневого рядуСодержание книги Поиск на нашем сайте
Теорема Абеля. 1) Якщо степеневий ряд (7.16) збіжний при деякому значенні 2) Якщо степеневий ряд розбіжний при деякому значенні Оскільки за припущенням числовий ряд
збіжний, то його загальний член Перепишемо степеневий ряд (7.16) у вигляді
і розглянемо ряд з абсолютних величин його членів
Члени цього ряду менші ніж відповідні члени ряду
При Оскільки члени ряду (7.19) менші ніж відповідні члени ряду (7.20), то ряд (7.19) теж збіжний, а це означає, що і ряд (7.18) чи ряд (7.16) збіжний абсолютно. 2) Доведемо другу частину теореми: нехай у деякій точці Дійсно, якби в якій-небудь точці Теорема Абеля дозволяє зробити висновок про розташування точок збіжності і розбіжності степеневого ряду: якщо З цього можна з’ясувати, що існує таке число Теорема 7.3. Для будь-якого степеневого ряду (7.16) існує таке додатне число Для доведення розглянемо ряд, складений з абсолютних величин членів даного ряду
Як відомо, якщо ряд (7.21) збіжний, ряд (7.16) також збіжний і при цьому абсолютно. Для дослідження ряду (7.21) застосуємо ознаку Даламбера:
Припустимо, що існує Тоді Очевидно, що ряд (7.21) збіжний при Якщо ж Таким чином, число R
є радіус збіжності степеневого ряду (7.16). Проміжок У випадку, якщо Можна показати, що степеневий ряд (7.15) збіжний при
де Поведінку ряду в точках Інтервал збіжності степеневого ряду (7.15) зображений схемою на рис. 7.2.
Рис. 7.2.
Якщо щодо дослідження ряду (7.21) застосувати радикальну ознаку Коші, можна одержати іншу формулу для обчислення радіуса інтервалу збіжності степеневого ряду:
Зауваження 1. Якщо при обчисленні радіуса інтервалу збіжності по формулах (7.22) чи (7.23) одержимо, що Зауваження 2. Область збіжності степеневого ряду і його інтервал збіжності можуть розрізнятися тільки крайніми точками. Зауваження. 3. Якщо степеневі ряди містять у собі тільки парні чи непарні степені Приклад 7.11. Знайти області збіжності степеневих рядів: а) Розв’язання. У випадку а): степеневий ряд містить у собі всі степені двочлена
Для нього Знайдемо радіус інтервалу збіжності ряду за формулою (7.22). Одержимо
Ряд збіжний на інтервалі, зображеному на рис. 7.3.
Рис. 7.3. Визначимо поведінку ряду в крайніх точках інтервалу. При
Отже, ряд розбіжний. При Отже, заданий ряд збіжний для усіх У випадку б): степеневий ряд містить у собі всі степені x і має вигляд
Для нього За формулою (7.22)
Отже, даний степеневий ряд збіжний на всій числовій прямій. У випадку в): степеневий ряд містить у собі тільки непарні степені x і має вигляд
Дослідимо ряд з модулів членів даного ряду, застосувавши ознаку Даламбера. Оскільки то Досліджуємо поведінку ряду на кінцях інтервалу збіжності. Підставляючи в степеневий ряд
При Отже, заданий ряд збіжний на відрізку [–1;1].
Наведемо властивості степеневих рядів. 1. Сума степеневого ряду 2. Степеневий ряд можна почленно диференціювати чи інтегрувати, при цьому радіус його інтервалу збіжності не порушиться. Може змінитися поведінка ряду тільки в крайніх точках області збіжності. Причому, якщо для степеневого ряду (7.16)
Властивості справедливі і для ряду (7.15). Так, для ряду
Інтегруючи почленно рівність (7.24) на відрізку
Ряди Тейлора і Маклорена Дотепер визначали область збіжності степеневого ряду. Знаємо, що сума степеневого ряду неперервна в його області збіжності. Поставимо обернену задачу: за заданою неперервною функцією Нехай неперервна функція
Права частина рівності (7.26) диференційована скільки завгодно раз, значить ліва частина цієї рівності, тобто функція Це перша вимога, якій повинна задовольняти функція
...................................................................
Підставляючи в ці рівності
Звідки знаходимо
Підставляючи значення коефіцієнтів у рівності (7.26), одержуємо
Степеневий ряд, коефіцієнти якого рівні відповідно При Якщо функція Але ряд Тейлора, складений для функції Назвемо різницю між функцією
Теорема 7.4. Для того, щоб функція 1) 2) Необхідність виконання першої умови очевидна. Необхідність виконання другої умови легко довести. Нехай Тоді Переходячи до границі при
Аналогічно можна довести, що якщо Доведено, що залишковий член ряду може бути записаний у вигляді
Це одна з форм залишкового члена ряду (форма Лагранжа), яка дозволяє оцінювати його при
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 629; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.215.149 (0.006 с.) |

 , не рівному нулю, то він абсолютно збіжний при всякому значенні
, не рівному нулю, то він абсолютно збіжний при всякому значенні 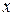 , для якого
, для якого  .
. .
.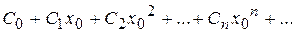 (7.17)
(7.17) при
при  , а це означає, що існує таке додатне число
, а це означає, що існує таке додатне число  , що всі члени ряду за абсолютним значенням менше
, що всі члени ряду за абсолютним значенням менше  (7.18)
(7.18)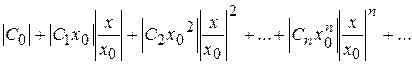 . (7.19)
. (7.19) . (7.20)
. (7.20) і, отже, збіжний.
і, отже, збіжний.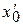 ряд (7.17) розбіжний. Тоді він буде розбіжним в будь-якій точці
ряд (7.17) розбіжний. Тоді він буде розбіжним в будь-якій точці  .
. , але це суперечить умові, що в точці
, але це суперечить умові, що в точці  заповнений точками абсолютної збіжності. Якщо
заповнений точками абсолютної збіжності. Якщо  і вся напівпряма уліво від точки –
і вся напівпряма уліво від точки –  , що при
, що при  маємо точки абсолютної збіжності і при
маємо точки абсолютної збіжності і при  – точки розбіжності. Виконується наступна теорема про будову області збіжності степеневого ряду.
– точки розбіжності. Виконується наступна теорема про будову області збіжності степеневого ряду. . (7.21)
. (7.21) .
. .
. .
. , тобто при
, тобто при  , тобто
, тобто  (7.22)
(7.22) називається інтервалом збіжності степеневого ряду.
називається інтервалом збіжності степеневого ряду. питання про збіжність ряду залишається відкритим, потрібно досліджувати конкретний числовий ряд, який отримаємо, якщо підставимо в заданий степеневий ряд значення
питання про збіжність ряду залишається відкритим, потрібно досліджувати конкретний числовий ряд, який отримаємо, якщо підставимо в заданий степеневий ряд значення  .
. , тобто для всіх
, тобто для всіх 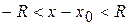 чи
чи  ,
,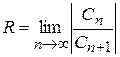 .
. потрібно досліджувати додатково.
потрібно досліджувати додатково.
 . (7.23)
. (7.23) , то, ряд збіжний тільки в одній точці. Якщо ж одержимо
, то, ряд збіжний тільки в одній точці. Якщо ж одержимо 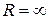 – ряд збіжний на всій числовій прямій.
– ряд збіжний на всій числовій прямій. , користуватися формулами (7.22), (7.23) не можна. У таких випадках інтервал збіжності степеневого ряду визначають, користуючись безпосередньо ознакою Даламбера.
, користуватися формулами (7.22), (7.23) не можна. У таких випадках інтервал збіжності степеневого ряду визначають, користуючись безпосередньо ознакою Даламбера. ; б)
; б)  ; в)
; в)  .
. і має вигляд
і має вигляд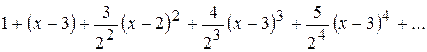 .
.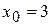 ,
,  ,
,  .
. .
.
 ряд приймає вигляд
ряд приймає вигляд  і є знакопочережним. Досліджуючи його за ознакою Лейбніца, знайдемо що
і є знакопочережним. Досліджуючи його за ознакою Лейбніца, знайдемо що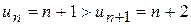 ,
,  .
. одержимо ряд
одержимо ряд  , що також розбіжний, тому що для нього не виконується необхідна ознака збіжності ряду.
, що також розбіжний, тому що для нього не виконується необхідна ознака збіжності ряду. .
. .
. ,
,  ,
,  .
.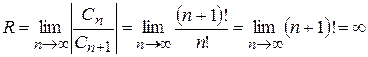 .
.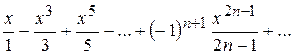 .
. ,
,  ,
,
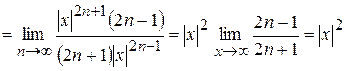 . При
. При  ряд збіжний. Розв’язуючи нерівність, знайдемо, що
ряд збіжний. Розв’язуючи нерівність, знайдемо, що  чи
чи  – інтервал збіжності даного ряду.
– інтервал збіжності даного ряду. , одержимо знакопочережний ряд
, одержимо знакопочережний ряд  , що за ознакою Лейбніца збіжний, тому що для нього
, що за ознакою Лейбніца збіжний, тому що для нього і
і 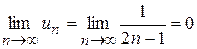 .
. , що також є знакопочережним і збіжним.
, що також є знакопочережним і збіжним.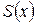 є функцією неперервною в будь-якій точці області збіжності.
є функцією неперервною в будь-якій точці області збіжності.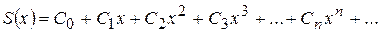
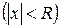 ,
, ,
, 

 сумою на інтервалі (–1;1) є функція
сумою на інтервалі (–1;1) є функція  , тобто
, тобто
 . (7.24)
. (7.24) , де
, де  або
або
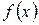 знайдемо степеневий ряд, що є збіжним, сума якого у всіх точках області збіжності збігається зі значеннями функції
знайдемо степеневий ряд, що є збіжним, сума якого у всіх точках області збіжності збігається зі значеннями функції  (7.26)
(7.26)
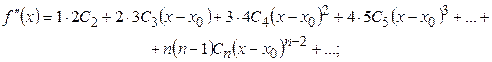

 .
. ;
; 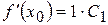 ;
; 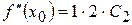 ;
; 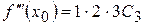 ;...;
;...;  .
. ;
;  ;
; 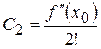 ;
;  ;...;
;...;  ,...
,... (7.27)
(7.27) , то цей ряд є рядом Тейлора функції
, то цей ряд є рядом Тейлора функції  ряду Тейлора функції
ряду Тейлора функції 
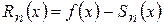 .
. була сумою складеного для неї ряду Тейлора, необхідно і достатньо виконання двох таких умов:
була сумою складеного для неї ряду Тейлора, необхідно і достатньо виконання двох таких умов: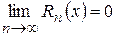 .
. – сума ряду Тейлора, а
– сума ряду Тейлора, а  ,
,  , одержуємо
, одержуємо ,
,  , де
, де  .
.


