
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розвинення функцій в ряд МаклоренаСодержание книги Поиск на нашем сайте
Щоб функцію 1. Знайти її похідні 2. Обчислити значення похідних у точці 3. Формально скласти ряд Тейлора (Маклорена); 4. Знайти область збіжності отриманого ряду; 5. Дослідити залишковий член ряду при Якщо Розглянемо
Такий ряд збіжний на всій числовій прямій. Залишковий член ряду
Розглянемо
Підставляючи
Ряд Маклорена для функції
Легко переконатися в тому, що такий ряд є збіжним на всій числовій прямій. Залишковий член ряду для функції
Розвинення в ряд функції
Розглянемо
Обчислимо значення функції і її похідних:
Одержимо степеневий ряд
Тоді
Формула (7.31) називається біноміальним рядом. При
Замінивши в останній рівності
Застосування степеневих рядів Степеневі ряди знаходять застосування в різних питаннях наближених обчислень.
Обчислення значень функцій. Для обчислення наближених значень функції з заданою точністю зручно використовувати ряди в тому випадку, коли відповідний ряд є знакопочережним. Для знакопочережного ряду, що є збіжним, легко оцінити похибку наближеного значення суми – вона менше ніж абсолютне значення першого з відкинутих членів. Приклад 7.12. Обчислити Розв’язання. Скористаємося розвиненням у ряд функції
Підставляючи в рівність значення
Абсолютна величина четвертого члена цього ряду менше чим 0,0001. Тому для обчислення наближеного значення з точністю до 0,0001 досить узяти суму трьох перших членів ряду
Наближене обчислення визначених інтегралів. Багато інтегралів, що не беруться чи важко обчислюються за формулою Ньютона–Лейбніца, можна обчислити, розкладаючи підінтегральну функцію в ряд, а потім інтегруючи на даному відрізку не саму функцію, а її розвинення в ряд.
Приклад 7.13. Обчислити Розв’язання. Розкладемо підінтегральну функцію в степеневий ряд. Оскільки то одержимо
Отримали знакопочережний ряд, що задовольняє умові ознаки Лейбніца, отже, похибка при заміні суми ряду сумою його перших членів не перевищує абсолютної величини першого відкинутого члена. Якщо взяти
Доведення формули Ейлера. Якщо
Оскільки
або, розділяючи дійсні і уявні доданки:
Відповідно до розвинень (7.29) і (7.30) вирази в дужках рівні
Динамічні ряди В економічному аналізі деякі скінченні суми прийнято називати рядами. Прикладами таких сум можуть бути динамічні ряди. Динамічний ряд являє собою сукупність послідовних значень деякого показника, які характеризують його зміну у часі. Якщо показник відноситься до економічної системи чи організації, то таку область досліджень називають економічною динамікою. Динамічні ряди бувають моментні та інтервальні. Перші відповідають значенню показника в певний момент часу, другі характеризують показник за деякий період. Динамічні ряди бувають також стаціонарні і нестаціонарні. Стаціонарний динамічний ряд не має тенденції до зміни тренду, нестаціонарний (еволюційний) ряд має тренд, що змінюється. Поняття тренду зазвичай характеризує певну тенденцію до постійної зміни показника, який описують за допомогою динамічного ряду. Існує безліч способів для обчислення тренду. При аналізі динамічних рядів використовують також поняття сезонності (циклічності), яке характеризує будь-які періодичні коливання даного ряду, а також поняття випадкового відхилення. Випадкове відхилення, або випадкова компонента, зафіксовує одномоментні зміни динамічного ряду під дією будь-яких випадкових факторів та причин. Для усунення випадкових відхилень виконують вирівнювання динамічного ряду.
Зазвичай при введенні динамічного ряду його зображають в вигляді певної математичної моделі. Форми математичної моделі динамічного ряду можуть бути різними. Нехай
– деякий динамічний ряд і Можна записати декілька частинних моделей динамічного ряду, наприклад: модель тренду
де модель сезонності
де Існують більш складні моделі динамічних рядів, в тому числі моделі кривих росту, адаптивні, авторегресивні та ін. В загальному випадку кожен член динамічного ряду
де Аналіз динамічного процесу проводиться по наступній схемі. 1. Члени динамічного ряду коректуються спеціальною компонентою 2. Управляючу компоненту 3. Обчислюють регулярну компоненту 4. Знаходять сезонну компоненту 5. Знаходять оцінку похибки при обчисленні Дослідження динамічних рядів і економічних процесів з ними пов’язаних проводять за допомогою формул та методів теорії ймовірностей, математичної статистики та економетрії. Вправи
7.1. Дослідити на збіжність ряд, користуючись означенням збіжності ряду. Якщо ряд збіжний, знайти його суму: а) б) в) г) д) є) 7.2. Перевірити необхідну ознаку збіжності ряду: а) в) д) 7.3–7.29. Застосовуючи достатні ознаки збіжності числових додатніх рядів, дослідити на збіжність наступні ряди. 7.3. 7.5. 7.7. 7.9. 7.11. 7.13. 7.14. 7.15. 7.16. 7.17. 7.18. 7.19. 7.20. 7.22. 7.24. 7.26. 7.28. 7.30–7.36. Дослідити на збіжність наступні знакозмінні ряди. 7.30. 7.32. 7.34. 7.35. 7.36. 7.37. Знайти суму рядів: а) б) в) 7.38–7.44. Дослідити на абсолютну та умовну збіжність наступні ряди. 7.38. 7.40. 7.42. 7.44. 7.45–7.49. Знайти області збіжності (абсолютної та умовної) наступних функціональних рядів. 7.45. 7.47. 7.49. 7.50–7.54. Дослідити послідовності на рівномірну збіжність на вказаному проміжку. 7.50. 7.51. 7.52. 7.53. 7.54. 7.55. Дослідити на збіжність 7.56. Дослідити на збіжність 7.57–7.62. Знайти область збіжності степеневих рядів. 7.57. 7.59. 7.61. 7.63. Розкласти в ряд Тейлора функцію 7.64–7.67. Розкласти в ряд Маклорена наступні функції. 7.64. 7.66. 7.68. Обчислити приблизно, використовуючи розвинення в степеневий ряд відповідної функції: а) 7.69. Обчислити наближено 7.70. Обчислити наближено
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.203.204 (0.01 с.) |

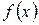 розкласти в ряд Тейлора (зокрема, у ряд Маклорена), потрібно:
розкласти в ряд Тейлора (зокрема, у ряд Маклорена), потрібно: ;
; (для ряду Маклорена
(для ряду Маклорена  );
); .
.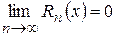 , то для функції
, то для функції  . Тоді:
. Тоді:  . Звідки одержуємо
. Звідки одержуємо  . Ряд Маклорена для функції
. Ряд Маклорена для функції  має вигляд
має вигляд .
. має вигляд
має вигляд 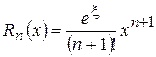 , де
, де 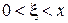 .
.  , тому що
, тому що  (як загальний член збіжного ряду). Тому справедлива рівність
(як загальний член збіжного ряду). Тому справедлива рівність
 . (7.28)
. (7.28) . Тоді
. Тоді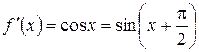 ;
;  ;
;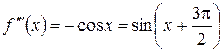 ;
;  ;...
;...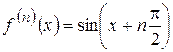 .
. .
. .
. , де
, де 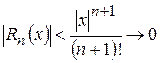 при будь-якому x, тоді
при будь-якому x, тоді (7.29)
(7.29) можна одержати шляхом диференціювання ряду для
можна одержати шляхом диференціювання ряду для  . (7.30)
. (7.30) , де
, де  – будь-яке дійсне число:
– будь-яке дійсне число: ;
;  ;
; ;...
;...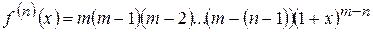 .
. ,
, 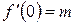 ,
,  ,
,  ,...
,...  .
.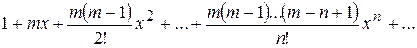

 . (7.31)
. (7.31) маємо геометричний ряд
маємо геометричний ряд
 .
.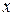 на
на 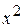 і, інтегруючи, одержимо розвинення в ряд функції
і, інтегруючи, одержимо розвинення в ряд функції 

 з точністю до 0,0001.
з точністю до 0,0001. :
:
 .
. , одержуємо ряд для обчислення
, одержуємо ряд для обчислення 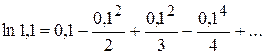 .
. .
. .
.


 , отримаємо похибку, меншу ніж
, отримаємо похибку, меншу ніж  . Звідси випливає, що обмеживши тільки двома доданками, одержимо наближене значення інтеграла з точністю до 0,01:
. Звідси випливає, що обмеживши тільки двома доданками, одержимо наближене значення інтеграла з точністю до 0,01: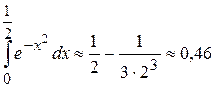 .
. . При цьому ряд є збіжним для будь-якого
. При цьому ряд є збіжним для будь-якого 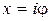 , де
, де 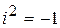 , одержимо
, одержимо .
.


 …, підставляючи ці значення в розвинення для
…, підставляючи ці значення в розвинення для  , маємо
, маємо
 .
. і
і  відповідно, а це означає, що
відповідно, а це означає, що .
. ,
,  ,
, – його спрощений запис.
– його спрощений запис. ,
, – часовий тренд даного виду,
– часовий тренд даного виду,  – випадкова компонента;
– випадкова компонента; ,
, – періодична сезонна складова.
– періодична сезонна складова. ,
,  можна представити в адитивній формі:
можна представити в адитивній формі: ,
,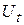 – тренд динамічного ряду – регулярна компонента, яка характеризує загальну тенденцію,
– тренд динамічного ряду – регулярна компонента, яка характеризує загальну тенденцію,  – сезонна (циклічна) компонента,
– сезонна (циклічна) компонента,  – випадкова компонента, яка утворюється під впливом різних (як правило, невідомих) причин,
– випадкова компонента, яка утворюється під впливом різних (як правило, невідомих) причин,  – компонента, яка забезпечує відповідність елементів динамічного ряду,
– компонента, яка забезпечує відповідність елементів динамічного ряду,  – управляюча компонента, за допомогою якої впливають на члени динамічного ряду з метою формування в майбутньому його траєкторії.
– управляюча компонента, за допомогою якої впливають на члени динамічного ряду з метою формування в майбутньому його траєкторії. .
. ;
; ;
; ;
; ;
; ;
; .
. ; б)
; б)  ;
; ; г)
; г)  ;
; ; є)
; є)  .
. . 7.4.
. 7.4.  .
. . 7.6.
. 7.6.  .
. . 7.8.
. 7.8.  .
. . 7.10.
. 7.10.  .
. . 7.12.
. 7.12.  .
. .
. .
. .
. .
. .
.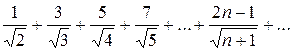 .
. .
. . 7.21.
. 7.21.  .
. . 7.23.
. 7.23.  .
. . 7.25.
. 7.25.  .
. . 7.27.
. 7.27.  .
. . 7.29.
. 7.29.  .
. . 7.31.
. 7.31.  .
. . 7.33.
. 7.33. 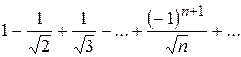 .
.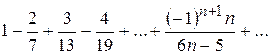 .
. .
. .
.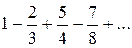 ;
; ;
; .
. . 7.39.
. 7.39.  .
. . 7.41.
. 7.41.  .
. . 7.43.
. 7.43.  .
. .
. . 7.46.
. 7.46.  .
.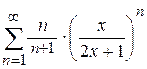 . 7.48.
. 7.48.  .
. .
.
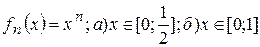 .
. .
. .
. .
. .
. , і, якщо можна, знайти суму, замінивши її сумою перших двох членів ряду. Оцінити похибку.
, і, якщо можна, знайти суму, замінивши її сумою перших двох членів ряду. Оцінити похибку. і знайти суму з точністю до 0,01.
і знайти суму з точністю до 0,01. . 7.58.
. 7.58.  .
. . 7.60.
. 7.60.  .
. . 7.62.
. 7.62. 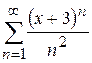 .
. за степенями
за степенями  .
. . 7.65.
. 7.65.  .
. . 7.67.
. 7.67.  .
. ; б)
; б)  .
. з точністю до 0,001.
з точністю до 0,001. з точністю до 0,1.
з точністю до 0,1.


