
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знакопочережні числові ряди. Ознака ЛейбніцаСодержание книги Поиск на нашем сайте
Розглянемо ряд, у якого два будь-яких сусідніх члени мають протилежні знаки. Такий ряд називається знакопочережним. Його можна записати у вигляді
де Знакопочережними, наприклад, є ряди:
Ознака Лейбніца. Якщо для знакопочережного ряду (7.9) виконуються умови: 1) 2) то цей ряд збіжний, сума його додатня і не перевищує значення першого члена. Доведемо, що при виконанні умов ознаки Лейбніца для ряду (7.9) існує границя послідовності частинних сум, тобто Розглянемо спочатку частинні суми ряду з парним числом членів:
Оскільки кожна з дужок за першою умовою додатня, то послідовність часткових сум
Очевидно, що Нехай Покажемо, що послідовність частинних сум з непарним числом членів має ту ж границю. Оскільки Зазначимо, що для суми Непарну частинну суму можна записати у вигляді:
звідки видно, що Зазначимо ще одну властивість знакопочережного ряду, що має велике практичне застосування. Нехай ряд
Різниця Таким чином, заміняючи суму ряду його частинною сумою, одержуємо похибку, абсолютна величина якої менше від абсолютної величини першого відкинутого члена ряду, тобто
Приклад 7.8. Дослідити на збіжність ряд Розв’язання. Порівняємо модулі сусідніх членів ряду, одержимо
тобто перша умова ознаки Лейбніца виконується. Оскільки Приклад 7.9. Скільки членів ряду, що є збіжним
потрібно взяти, щоб обчислити його суму з точністю до 0,001? Розв’язання. Оскільки згідно (7.10)
то для забезпечення необхідної точності потрібно при обчисленні суми в першу чергу відкинути той член, абсолютна величина якого менше 0,001. Обчислюючи члени ряду, послідовно, бачимо, що
Знакозмінні числові ряди Ряди з довільним розподілом знаків їхніх членів називаються знакозмінними. Будемо записувати такі ряди у вигляді
вважаючи при цьому що числа Зазначимо, що знакопочережні ряди є окремим випадком знакозмінних рядів. Розглянемо ряд, складений з модулів членів знакозмінного ряду (7.11)
усі члени якого додатні. Теорема 7.2. Знакозмінний ряд (7.11) збіжний, якщо збіжним є ряд, складений з модулів його членів (7.12). Нехай ряд (7.12) збігається. Запишемо очевидну нерівність
У нерівності (7.13) величина Але тоді на підставі властивостей рядів, що збігаються, можна стверджувати, що буде збігатися і ряд
Зазначимо, що зворотнє твердження невірне. Якщо даний знакозмінний ряд збіжний, то ряд, складений з модулів його членів не обов'язково збіжний, цей ряд може бути і розбіжним. Усі знакозмінні ряди, що є збіжними можна розділити на дві групи. До першої групи відносяться такі ряди, що є збіжними, для яких ряди, складені з модулів їхніх членів, також є збіжними. Такі ряди називаються абсолютно збіжними. До другої групи відносяться знакозмінні ряди, що є збіжними, для яких ряд, складений з модулів їхніх членів, розбіжний. Такі знакозмінні ряди називаються умовно збіжними. Так, ряд Можна показати, що в знакозмінному ряді, що є збіжним, будь-яке угруповання членів ряду, не змінює їхнього порядку, зберігає збіжність ряду і значення його суми. Для абсолютно збіжних рядів можна довільно переставляти члени ряду. Ряд отриманий при цьому є також абсолютно збіжним і має ту ж суму. Умовно збіжні ряди такою властивістю не володіють. Переконаємося в цьому на прикладі. Знаємо, що ряд
збіжний умовно. Позначимо його суму
Групуючи його члени, одержимо ряд
або
Перестановкою членів ряду Як показав німецький математик Ріман, перестановкою членів умовно збіжного ряду можна одержати ряд, що є збіжним, і має будь-яку наперед задану суму, і навіть розбіжний ряд.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.24.49 (0.013 с.) |

 , (7.9)
, (7.9) .
. ;
;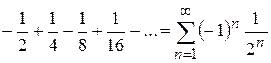 .
. ;
;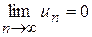 ,
,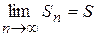 .
.
 зростаюча. Покажемо, що вона обмежена. Для цього запишемо:
зростаюча. Покажемо, що вона обмежена. Для цього запишемо: .
.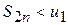 . Отже, послідовність частинних сум
. Отже, послідовність частинних сум  .
.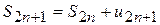 і
і  при
при  (за умовою), то
(за умовою), то  , тобто послідовність усіх частинних сум знакопочережного ряду (7.9) має скінченну границю і, отже, ряд збіжний.
, тобто послідовність усіх частинних сум знакопочережного ряду (7.9) має скінченну границю і, отже, ряд збіжний. ряду (7.9) справедливе співвідношення
ряду (7.9) справедливе співвідношення  . Для парних частинних сум це показали в доведенні ознаки.
. Для парних частинних сум це показали в доведенні ознаки. ,
, .
. , тоді
, тоді .
. – залишок ряду, у свою чергу є сумою ряду, і, отже
– залишок ряду, у свою чергу є сумою ряду, і, отже  .
.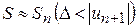 . (7.10)
. (7.10)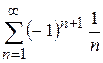 .
. ,
,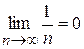 , то і друга умова ознаки Лейбніца виконується, отже, даний ряд збіжний.
, то і друга умова ознаки Лейбніца виконується, отже, даний ряд збіжний.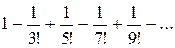
 ,
, , тому
, тому 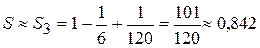
 , тобто необхідно взяти три члени ряду.
, тобто необхідно взяти три члени ряду. , (7.11)
, (7.11) ,
, 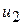 ,... можуть бути як додатніми, так і від'ємними.
,... можуть бути як додатніми, так і від'ємними.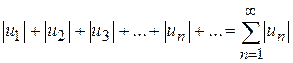 , (7.12)
, (7.12)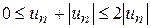 . (7.13)
. (7.13) є загальним членом збіжного ряду
є загальним членом збіжного ряду 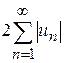 , а величина
, а величина  – загальним членом невід’ємного ряду
– загальним членом невід’ємного ряду  , що також є збіжним на підставі ознаки порівняння.
, що також є збіжним на підставі ознаки порівняння. .
. збіжний абсолютно, а ряд
збіжний абсолютно, а ряд 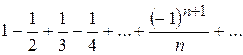
 .
.
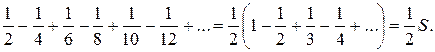
 одержали ряд, сума якого в два рази менше ніж сума даного ряду.
одержали ряд, сума якого в два рази менше ніж сума даного ряду.


