
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття про потрійний інтегралСодержание книги Поиск на нашем сайте
Нехай у деякій замкнутій області Означення 6.1. Потрійним інтегралом функції
Якщо невід’ємна функція
Ця рівність є механічним змістом потрійного інтеграла. Якщо
Враховуючи, що елемент об'єму
Виходячи з означення потрійного інтеграла можна сформулювати його основні властивості. 1) Сталий множник можна виносити за знак потрійного інтеграла, тобто
2) Потрійний інтеграл від суми функцій дорівнює сумі потрійних інтегралів від доданків за тією ж областю:
3) Якщо область
4) Якщо в області
5) Якщо в області
6) Модуль потрійного інтеграла не перевищує потрійного інтеграла модуля функції, що інтегрується, тобто Для потрійного інтеграла можна довести теорему про середнє значення. Теорема 6.3. Якщо функція
де Обчислення потрійних інтегралів відбувається шляхом послідовного обчислення інтегралів меншої кратності. За аналогією до подвійного інтеграла (рис. 6.17) будемо мати
Якщо, крім того, проекцією області на площину є область, яка визначається системою нерівностей
Рис. 6.17.
При обчисленні потрійного інтеграла за формулою (6.20) за допомогою повторного інтеграла спочатку обчислюється внутрішній інтеграл за змінною Зокрема, якщо область
Приклад 6.9. Обчислити інтеграл
Розв’язання. Область Одержуємо
Заміна змінних в потрійному інтегралі Нехай області
де якобіан має вигляд Найчастіше використовують циліндричну і сферичну системи координат, а також їх узагальнення. Циліндрична система координат:
Загальні циліндричні координати:
Узагальнені циліндричні координати:
Сферичні координати:
Загальні сферичні координати:
Узагальнені сферичні координати:
Застосування потрійного інтеграла у фізиці До обчислення потрійних інтегралів приводять задачі, пов'язані з неперервним розподілом маси в просторовій області. Якщо відома щільність розподілу маси
моментів інерції відносно координатних вісей:
моментів інерції відносно координатних площин:
полярного моменту інерції
координат центра мас:
Вправи 6.1. Побудувати області, площі яких виражаються інтегралами: 1) Змінити порядок інтегрування й обчислити площі. 6.2. Змінити порядок інтегрування: а) б) в) 6.3. Представити подвійний інтеграл а) б) в) 6.4. Обчислити 6.5. Обчислити 6.6. Обчислити інтеграли: а) б) в) г) д) 6.7. Знайти об’єм тіла, обмеженого поверхнями (за допомогою подвійного інтегралу): а) б) в) 6.8. Знайти площу області, яка обмежена кривими: а) 6.9. Знайти об'єм тіла, обмеженого еліптичним параболоїдом 6.10. Обчислити об'єм тіла, обмеженого площиною 6.11. Обчислити координати центра ваги фігури, обмеженої кривими: а) б) в) г) 6.12. Обчислити: а) б) в) г) д) 6.13. Обчислити 6.14. Знайти об’єм тіла, обмеженого поверхнями: а) б) в) 6.15. Визначити центр мас однорідного тіла, обмеженого поверхнею 6.16. Знайти масу тіла, обмеженого поверхнями: а) б) в)
Розділ 7. Ряди
|
|||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.175.166 (0.006 с.) |

 простору задана функція трьох змінних
простору задана функція трьох змінних  . Розіб'ємо область
. Розіб'ємо область 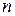 областей, що не мають загальних внутрішніх точок. У кожній області
областей, що не мають загальних внутрішніх точок. У кожній області  візьмемо довільно точку
візьмемо довільно точку  . Значення функції
. Значення функції  в точці помножимо на об'єм
в точці помножимо на об'єм 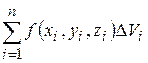 буде інтегральною сумою функції
буде інтегральною сумою функції  і ця границя існує, тобто
і ця границя існує, тобто . (6.17)
. (6.17) – відома щільність розподілу маси тіла,
– відома щільність розподілу маси тіла,  . (6.18)
. (6.18) , то
, то .
. у прямокутних координатах обчислюється за формулою
у прямокутних координатах обчислюється за формулою  , одержуємо формулу для обчислення об'єму тіла V за допомогою потрійного інтеграла:
, одержуємо формулу для обчислення об'єму тіла V за допомогою потрійного інтеграла: . (6.19)
. (6.19) .
. .
. .
. , то
, то .
. , то
, то  .
. .
. , що
, що ,
, – об'єм даної області.
– об'єм даної області. .
. то
то . (6.20)
. (6.20)
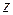 при сталих
при сталих 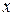 і
і  , а потім отримана функція послідовно інтегрується за змінною
, а потім отримана функція послідовно інтегрується за змінною  . (6.21)
. (6.21) по області, що обмежена площинами
по області, що обмежена площинами  ,
,  ,
,  ,
,  (рис. 6.18).
(рис. 6.18). Рис. 6.18.
Рис. 6.18.
 проектується на площину
проектується на площину  в область, обмежену прямими
в область, обмежену прямими  , яку можна записати за допомогою системи нерівностей
, яку можна записати за допомогою системи нерівностей 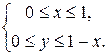


 в системі координат
в системі координат  відповідає область
відповідає область  в системі координат
в системі координат  , тоді справедлива формула:
, тоді справедлива формула:
 .
.

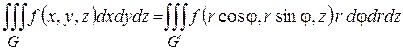 .
.
 .
.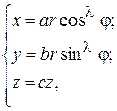
 .
.



 .
.
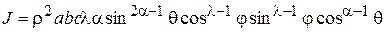 .
. в області
в області  ,
,  ,
,  ;
; ,
,  ,
, ;
; ,
,  ,
, ;
; ;
; ,
, 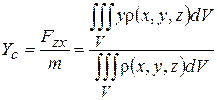 ,
, .
. ; 2)
; 2)  .
. ;
; ;
; .
. за допомогою повторних із зовнішнім інтегруванням по
за допомогою повторних із зовнішнім інтегруванням по  :
:  ,
,  ,
,  ;
; ,
,  ;
; ,
,  ,
, 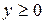 .
. , де
, де  – криволінійний трикутник, обмежений параболою
– криволінійний трикутник, обмежений параболою  і прямими
і прямими  .
. , де
, де  – частина кола радіуса a з центром у точці (0;0), що лежить у першій чверті.
– частина кола радіуса a з центром у точці (0;0), що лежить у першій чверті. ,
,  ,
,  ;
; ;
; ,
,  ,
,  ,
,  ;
; ; є)
; є)  .
. ,
,  ;
; ,
,  ,
,  ,
,  ,
,  ,
,  ; б)
; б)  ; в)
; в)  .
. , площиною
, площиною  , циліндром
, циліндром  і конусом
і конусом  .
. ,
,  ;
; ,
,  ;
; ,
,  ,
,  ,
,  ;
; ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , де
, де  .
. ,
,  ;
; ,
,  ,
,  ,
,  ,
,  і координатними площинами.
і координатними площинами. ,
,  ;
; ,
,  ,
,  ;
; ,
,  ,
,  .
.


