
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обчислення подвійного інтегралаСодержание книги Поиск на нашем сайте
Будемо називати область
Аналогічно область
Теорема 6.2. Подвійний інтеграл
Очевидно, що для функції
тобто подвійний інтеграл не змінюється від зміни порядку інтегрування. Зауваження. Якщо
то
Можна запропонувати такий порядок обчислення подвійного інтеграла. 1. Побудувати плоску область 2. Розставити границі інтегрування у повторному інтегралі. 3. Обчислити внутрішній інтеграл. 4. Обчислити зовнішній інтеграл. Приклад 6.2. Обчислити подвійний інтеграл
Розв’язання. Якщо розглянути область як просту відносно Тоді Обчислимо внутрішній інтеграл:
Проінтегруємо отриману функцію за аргументом
Звичайно при обчисленні інтеграла запис не переривають і записують так:
Якщо розглянути область Тоді
Нехай область інтегрування Таку область можна задати такою системою нерівностей:
Введемо поняття подвійного інтеграла для функції Складемо інтегральну суму для заданої функції. Оскільки границя інтегральної суми не залежить від способу розбивання області Інтегральна сума для даної функції буде мати вигляд:
Якщо існує границя такої інтегральної суми за умови, що площа найбільшої ділянки розбиття прямує до нуля, то вона і буде називатися подвійним інтегралом функції
Рис. 6.9.
Обчислимо елемент площі у полярній системі координат як площу прямокутника (рис. 6.9):
Тоді формула (6.5) набуде вигляду
Для обчислення подвійного інтеграла його потрібно замінити повторним. Якщо область
Іноді подвійний інтеграл у полярних координатах обчислюється набагато простіше, ніж у декартових. Тому треба вміти виконувати перехід від декартових координат до полярних в самому інтегралі, застосовуючи формули переходу
Тоді
Приклад 6.3. Обчислити
Розв’язання. Зазначимо що відомими методами не можливо обчислити інтеграл від функції
Тоді
Зауваження. До полярної системи координат має сенс переходити у випадку, якщо область інтегрування обмежена колом чи її частиною або в підінтегральній функції міститься вираз
Застосування подвійного інтеграла в геометрії Площа плоскої фігури. На підставі властивостей подвійного інтеграла Для Отже, у прямокутних координатах
У полярній системі координат
Приклад 6.4. Обчислити площу фігури, що обмежена лініями Розв’язання. Розглянемо область Отже, Тоді
Приклад 6.5. Обчислити площу фігури, що обмежена лініями Розв’язання. Перетворимо перші два рівняння до канонічного вигляду, одержимо
Як видно з рисунка, дану площу не можна обчислити за допомогою одного подвійного інтеграла в прямокутних координатах. В полярній системі координат область є простою по Очевидно, що Тоді
Об'єм тіла. Виходячи з геометричного змісту подвійного інтеграла, об'єм тіла з основою
Приклад 6.6. Знайти об'єм тіла Розв’язання. Дане тіло є циліндричним з основою В силу симетричності тіла відносно координатної площини
Оскільки
Приклад 6.7. Обчислити об'єм тіла, обмеженого поверхнями
Розв’язання. Оскільки основою тіла в площині де Тоді Отже
Площа поверхні. Розглянемо поверхню, задану рівнянням
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 714; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.187.60 (0.008 с.) |

 простою відносно
простою відносно 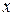 , якщо будь-яка пряма, перпендикулярна до вісі
, якщо будь-яка пряма, перпендикулярна до вісі  перетинає область не більш, ніж у двох точках (рис. 6.5). Таку область можна задати за допомогою системи нерівностей:
перетинає область не більш, ніж у двох точках (рис. 6.5). Таку область можна задати за допомогою системи нерівностей:
 , якщо будь-яка пряма, перпендикулярна до вісі
, якщо будь-яка пряма, перпендикулярна до вісі  перетинає область не більш, ніж у двох точках (рис. 6.6). Таку область можна задати за допомогою системи нерівностей:
перетинає область не більш, ніж у двох точках (рис. 6.6). Таку область можна задати за допомогою системи нерівностей:


 по простій області може бути обчислений за допомогою повторного інтегрування за однією з формул:
по простій області може бути обчислений за допомогою повторного інтегрування за однією з формул: ; (6.3)
; (6.3) . (6.4)
. (6.4) неперервної в області
неперервної в області 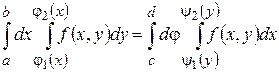 ,
, й область
й область 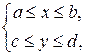
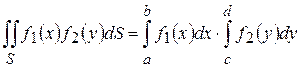 .
. по області, що обмежена лініями
по області, що обмежена лініями  ,
, 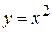 ,
, 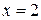 (рис. 6.7).
(рис. 6.7). Рис. 6.7.
Рис. 6.7.

 .
. .
. :
: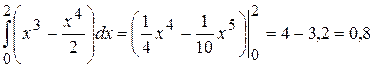 .
.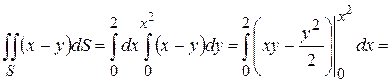





 , якщо будь-який промінь, що проходить через внутрішню точку області, перетинає її межі не більш, ніж у двох точках (рис. 6.8).
, якщо будь-який промінь, що проходить через внутрішню точку області, перетинає її межі не більш, ніж у двох точках (рис. 6.8).
 Рис. 6.8.
Рис. 6.8.
 заданої в полярній системі координат.
заданої в полярній системі координат. і концентричними колами
і концентричними колами  ,
,  ,...,
,...,  (рис. 6.9).
(рис. 6.9). .
. . (6.5)
. (6.5)
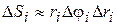 .
. . (6.6)
. (6.6) . (6.7)
. (6.7) ,
,  ,
,  .
. . (6.8)
. (6.8) по чверті кільця
по чверті кільця 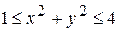 , що лежить у першому квадранті (рис. 6.10).
, що лежить у першому квадранті (рис. 6.10).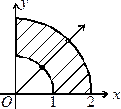 Рис. 6.10.
Рис. 6.10.
 за жодним з аргументів. У полярній системі координат інтеграл обчислюється просто. Область інтегрування обмежена колами
за жодним з аргументів. У полярній системі координат інтеграл обчислюється просто. Область інтегрування обмежена колами  і
і  , рівняння яких у полярній системі координат
, рівняння яких у полярній системі координат  і
і  . Область інтегрування
. Область інтегрування

 .
. .
. .
. підінтегральна функція
підінтегральна функція  і виходячи з геометричного змісту подвійного інтеграла одержимо об'єм циліндричного тіла висотою
і виходячи з геометричного змісту подвійного інтеграла одержимо об'єм циліндричного тіла висотою  , що дорівнює площі основи тіла, тобто
, що дорівнює площі основи тіла, тобто  (од. куб.) =
(од. куб.) =  . (6.9)
. (6.9) . (6.10)
. (6.10) Рис. 6.11.
Рис. 6.11.
 ,
,  (рис. 6.11).
(рис. 6.11).


 ,
,  ,
,  ,
,  ,
,  . Перше рівняння визначає коло з центром у точці (1;0) з радіусом
. Перше рівняння визначає коло з центром у точці (1;0) з радіусом  , друге рівняння також визначає коло з центром у точці (2;0) з радіусом
, друге рівняння також визначає коло з центром у точці (2;0) з радіусом 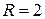 (рис. 6.12).
(рис. 6.12). Рис. 6.12.
Рис. 6.12.
 , а для другого відповідно
, а для другого відповідно  .
.

 (кв. од.)
(кв. од.) , бічною поверхнею, паралельною вісі
, бічною поверхнею, паралельною вісі 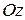 , обмеженого зверху поверхнею заданою рівнянням
, обмеженого зверху поверхнею заданою рівнянням  , може бути обчислений за формулою
, може бути обчислений за формулою . (6.10)
. (6.10) , обмеженого поверхнями
, обмеженого поверхнями  ,
,  ,
,  ,
,  (рис. 6.13).
(рис. 6.13). .
. можна обчислити об'єм тіла з основою
можна обчислити об'єм тіла з основою  , (рис. 6.14), потім результат подвоїти.
, (рис. 6.14), потім результат подвоїти.




 ,
,  , z=0 (рис. 6.15).
, z=0 (рис. 6.15). Рис. 6.15.
Рис. 6.15.
 . Тому
. Тому  ,
, . Область
. Область 
 .
. . (6.11)
. (6.11)


