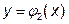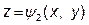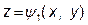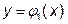Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтеграли по області, їх властивості, різновиди та деякі застосуванняСодержание книги
Поиск на нашем сайте
Інтеграли по області, їх властивості, різновиди та деякі застосування
Визначення інтеграла
Нехай в замкненій області D задана функція Область D довільним чином розіб’ємо на n частин D 1, D 2,..., Dn і в кожній частині візьмемо довільну точку: М 1, М 2,..., Мn. Позначимо Інтеграл по області D визначається як границя інтегральної суми за формулою
Якщо інтеграл від функції Достатньою умовою інтегрованості функції в замкненій обмеженої області D є її неперервність в цій області.
Основні властивості інтеграла по області Основні властивості інтеграла по області аналогічні властивостям визначеного інтеграла. Вкажемо ці властивості при умові інтегрованості відповідних функцій. 1. Якщо область D розбити на дві області D1 та D2 без спільних внутрішніх точок, тоді
2. Сталий множник можна виносити за знак інтеграла. 3. Інтеграл по області D від алгебраїчної суми скінченої кількості функцій дорівнює такій самій алгебраїчній сумі від кожної з цих функцій:
4. Якщо
5. 6. Якщо підінтегральна функція
7. Оцінка інтеграла по області. Якщо
8. Теорема про середнє. Якщо
Різновиди інтегралів по області
Інтегралам по області надають спеціальні назви і позначення в залежності від типу області. Якщо областю інтегрування є дуга АВ кривої L, то інтеграл називають криволінійним інтегралом першого роду і позначають так:
Оскільки мірою лінійної множини є довжина, то під знаком інтеграла замість
Якщо дуга АВ просторова, то
Криволінійний інтеграл першого роду не залежить від напряму інтегрування:
Якщо областю інтегрування буде деяка поверхня S, тоді інтеграл називають поверхневим інтегралом першого роду і позначають Оскільки мірою поверхневої множини є площа, то під знаком інтеграла замість
Якщо область інтегрування є плоскою поверхнею D, то
Такий інтеграл називають подвійним інтегралом. Інтеграл по просторовій області V називають потрійним інтегралом і позначають так:
Оскільки
Існують ще криволінійні та поверхневі інтегралидругого роду, які є різновидами інтеграла по орієнтованій області від вектор-функції. Їх позначають так:
де Криволінійний інтеграл 2 роду змінює свій знак при зміні напряму інтегрування:
Аналогічну властивість мають поверхневі інтеграли другого роду. Оскільки різні сторони поверхні відповідають різним напрямкам нормалі, то інтеграли, у яких областями інтегрування є різні сторони поверхні S, відрізняються знаками.
Обчислення подвійних інтегралів
Якщо область D на площині хОу правильна в напрямку осі Оу (див. мал. 1, а), то її аналітично можна описати нерівностями виду
і подвійний інтеграл зводиться до повторного за формулою:
Якщо область D на площині хОу правильна в напрямку осі Ох (див. мал. 1, б), то її аналітично можна описати нерівностями виду
і подвійний інтеграл зводиться до повторного за формулою:
Якщо область D на площині хОу правильна в напрямі осі Оу і в напрямі осі Ох (див. мал. 1, в), тоді мають місце рівності:
які означають, що подвійний інтеграл в цьому випадку можна обчислити за формулою (2) або (4). Для обчислення повторного інтеграла треба спочатку за формулою Ньютона-Лейбніца знайти внутрішній інтеграл за відповідною змінною інтегрування, а потім обчислити зовнішній інтеграл за іншою змінною інтегрування.
Y Y
c
в) D Мал.1
X Приклад 2. Визначити сумарний заряд Q пластинки, що обмежена лініями у = х 2, у 2 = х, 4 х + 4 у – 3 = 0, якщо щільність розподіленого поверхневого заряду Розв’язання. Згідно фізичному значенню інтеграла по області маємо:
Область інтегрування D зображена на мал. 2. Щоб одержати аналітичний опис заданої пластинки у вигляді нерівностей (3) розіб’ємо D на дві частини D 1 та D 2 прямою
y
Мал.2
З малюнка 2 одержуємо аналітичний опис областей:
Для цього в кожній області спочатку визначили сталі межі змінної у, а потім – нерівності для х шляхом визначення значень х, якщо рухатися через область за напрямом осі Ох. Отже,
Мал. 4 |
 |
1. Обчислити повторні інтеграли:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
2. Записати рівняння ліній, що обмежують області інтегрування заданих інтегралів та зобразити ці області:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 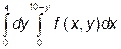 .
.
3. Перейти від подвійного інтеграла  до повторного:
до повторного:
а) D – трикутник з вершинами O (0, 0), А (1, 0), В (1, 1).
б) D – трапеція з вершинами O (0, 0), А (2, 0), В (1, 1), С (0, 1).
в) D – паралелограм з вершинами А (1, 5), В (2, 4), С (2, 7), D (1, 5).
г) D – параболічний сегмент, що обмежений параболою
у = х 2 та відрізком, який з’єднує точки параболи В (–1, 2) та
А (1, 2).
д) D – кругове кільце, що обмежене колами радіусів r = 1 та R = 3 із загальним центром O (0, 0).
4. Змінити порядок інтегрування
а)  ; б)
; б)  ; в)
; в)  .
.
5. Обчислити інтеграл  , якщо
, якщо
а) D – трикутник з вершинами O (0, 0), А (1, 1) та В (0, 1);
б) D – обмежена прямою, що проходить через точки
А (2, 0) та В (0, 2), і дугою кола з центром в точці С (0, 1), радіуса 1.
6. Обчислити інтеграл  , де D – область, що обмежена лініями у 2 = х, х = 0, у = 1.
, де D – область, що обмежена лініями у 2 = х, х = 0, у = 1.
7. Обчислити  , де D – область, що обмежена лініями
, де D – область, що обмежена лініями  , у = х.
, у = х.
8. Використовуючи перехід до полярних координат, обчислити інтеграли:
а) 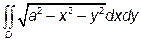 , D – півкруг радіуса а з центром в початку координат, що лежить вище осі Ох.
, D – півкруг радіуса а з центром в початку координат, що лежить вище осі Ох.
б)  ;
;
в) 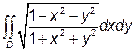 , D – визначається нерівностями
, D – визначається нерівностями 
г)  , D – частина кільця
, D – частина кільця 
д)  , D – круг
, D – круг  .
.
Основні поняття
Обчислення поверхневих інтегралів можна звести до обчислення відповідних подвійних інтегралів.
Якщо S – незамкнена поверхня, яка задається рівнянням z = q (x, y), а область D – проекція цієї поверхні на площину хОу, тоді
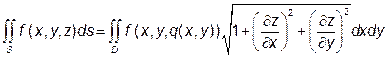 (1) )
(1) )
Якщо поверхня S замкнена, тоді її розбивають на дві незамкнені поверхні S 1 та S 2 так, щоб обидві вони проектувалися на одну область D площини хОу. Якщо рівнянням поверхні S 1 буде z = q 1(x, y), а рівнянням поверхні S 2 буде z = q 2(x, y), тоді
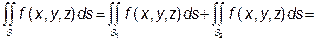

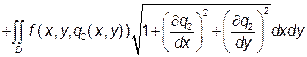 .
.
Приклад 4. Обчислити 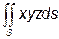 , де S – частина площини x + у + z = 1, яка лежить в першому октанті (мал. 5).
, де S – частина площини x + у + z = 1, яка лежить в першому октанті (мал. 5).
Розв’язання. В даному випадку рівнянням поверхні S буде z = 1 – x – y, її проекцією – областю D буде прямокутний трикутник обмежений лініями: x = 0, у = 0, х + у =1.
Поверхня S – незамкнена, тому за формулою (1) одержимо:
|
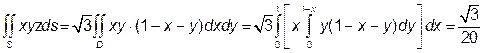
Приклад 5. Обчислити площу поверхні еліпсоїда обертання 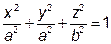 .
.
Розв’язання. Згідно властивості інтеграла по області 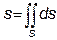 ,
,
де S є поверхня еліпсоїда, яку можна розбити на дві частини
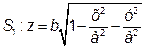 ;
;  .
.
Проекцією цих поверхонь на площину хОу буде круг D, який визначається системою нерівностей

Використовуючи симетрію еліпсоїда, одержимо:
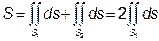 .
.
Оскільки
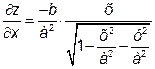 ,
, 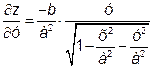 ,
,
то
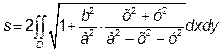 .
.
Перейдемо до полярних координат в подвійному інтегралі

Тому
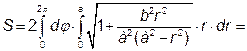

 |
1. Обчислити інтеграл 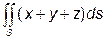 , де S – поверхня куба
, де S – поверхня куба 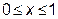 ;
; 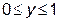 ;
; 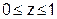 .
.
Рекомендація.
Шуканий інтеграл в 3 рази більше суми інтегралів по верхній та нижній граням куба.
2. Обчислити інтеграл  , де S – сфера
, де S – сфера
х 2 + у 2 + z 2 = а 2.
3. Обчислити інтеграл 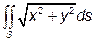 , де S – бокова поверхня конуса
, де S – бокова поверхня конуса 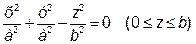
4. Обчислити інтеграли:
а) 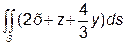 , де S – частина площини
, де S – частина площини 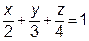 , що лежить в першому октанті.
, що лежить в першому октанті.
б)  , де S – півсфера
, де S – півсфера  .
.
5. Знайти масу сфери, якщо поверхнева густина в кожній точці дорівнює квадрату відстані цієї точки від деякого фіксованого діаметра сфери. (Відповідь:  ).
).
Рекомендація. Якщо зафіксувати будь-який діаметр сфери в площині z = 0, то поверхнева густина буде R 2 – х 2 – у 2.
Основні поняття
Нехай V деяка просторова область, що обмежена замкненою поверхнею S. Область V називають правильною за напрямом осі Оz, якщо вона має властивості:
1. будь-яка пряма, що паралельна осі Оz, перетинає поверхню S не більше ніж в двох точках;
2. уся область V проектується на площину хОу в правильну двовимірну область D.
Аналогічно визначаються правильні тривимірні області за напрямами осей Ох та Оу.
Область V, яка правильна за напрямами усіх трьох координатних осей, називають правильною.
Правильними тривимірними областями є еліпсоїди, піраміди, призми та інші тіла.
Якщо тривимірна область V правильна, то обмежуючу її поверхню S можна розбити на дві частини: нижню – S 1, рівняння якої 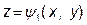 , та верхню S 2, рівняння якої
, та верхню S 2, рівняння якої 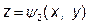 (див. мал. 6).
(див. мал. 6).
  

          
|
Обидві ці поверхні (отже, і сама область V) проектуються на площину хОу в правильну область D, межа якої точками А та В поділяється на дві криві з рівняннями  ,
,  .
.
Позначимо довільну точку області V через М (х, у, z), а її проекцію на площину хОу – N (х, у, 0).
При фіксованих х та у апліката z точки М, що знаходиться всередині області V, може змінюватись від 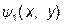 до
до 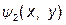 .
.
Якщо точка М пересувається всередині області V, то точка N пересувається всередині області D, а її координати (а тому і координати х, у точки М) повинні задовольняти нерівностям 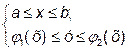 .
.
Отже, координати будь-якої точки 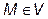 повинні задовольняти систему нерівностей
повинні задовольняти систему нерівностей
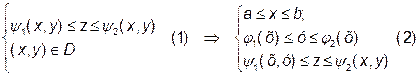 Системи (1) та (2) є аналітичним описом просторової області V.
Системи (1) та (2) є аналітичним описом просторової області V.
Якщо функції 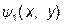 та
та  неперервні в замкненій області D площини хОу і область V описується системою виду (1), то обчислення потрійного інтеграла можна здійснити шляхом послідовного обчислення інтегралів меншої кратності за формулою:
неперервні в замкненій області D площини хОу і область V описується системою виду (1), то обчислення потрійного інтеграла можна здійснити шляхом послідовного обчислення інтегралів меншої кратності за формулою:
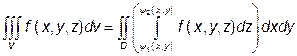
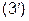
Якщо область V описується системою вигляд (2), то потрійний інтеграл обчислюють за формулою:
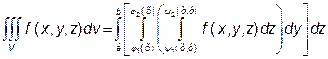
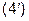
Ці формули найчастіше записують у вигляді:
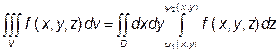 (3)
(3)
 , (4)
, (4)
відповідно.
Отже, аналітичний опис області V виду (2) дозволяє обчислення потрійного інтеграла звести до обчислення трикратного інтеграла, в якому: межі зовнішнього інтеграла – сталі; межі середнього інтеграла можуть залежати лише від змінної інтегрування зовнішнього інтеграла; межі внутрішнього інтеграла можуть залежати від змінних інтегрування середнього та зовнішнього інтегралів.
Для обчислення потрійного інтеграла в прямокутних координатах крім формул (3) та (4) часто використовують ще формули:
 (5)
(5)
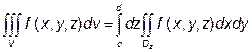 (6)
(6)
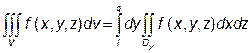 , (7)
, (7)
де Dx (Dz, Dу) – перетин області V площиною, яка паралельна площині уОz (площинам хОу та хОz, відповідно) і проходить через довільну точку інтервалу (а, b) (інтервалу (с, d) та (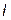 , q), відповідно) – інтервалу зовнішнього інтеграла.
, q), відповідно) – інтервалу зовнішнього інтеграла.
Ці формули часто спрощують обчислення потрійних інтегралів.
Приклад 6. Обчислити 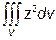 , де область V обмежена поверхнею обертання кривої
, де область V обмежена поверхнею обертання кривої  навколо осі Оz і площиною z = h (h > 0).
навколо осі Оz і площиною z = h (h > 0).
Розв’язування. Щоб одержати рівняння поверхні обертання заданої лінії навколо осі Оz, залишимо змінну z в рівнянні лінії  без зміни, а у замінимо на
без зміни, а у замінимо на 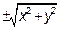 . Одержимо:
. Одержимо: 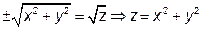 – рівняння параболоїда обертання.
– рівняння параболоїда обертання.
Проекцією області V на площину хОу буде круг х 2 + у 2 = h.
Заданий потрійний інтеграл можна обчислити за різними формулами.
Для застосування формули (4) використовуємо аналітичний опис області інтегрування V:
 .
.
Тоді одержимо: 
Обчислення інтеграла за цією формулою приводить до громіздких викладок.
Тому застосуємо формулу (6):
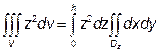 ,
,
де Dz є перетин області V площиною, яка перпендикулярна до осі Оz і лежить на висоті z, причому 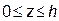 .
.
Перетин Dz буде кругом радіусом 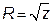 , що випливає із рівняння поверхні обертання х 2 + у 2 = z.
, що випливає із рівняння поверхні обертання х 2 + у 2 = z.
Внутрішній інтеграл
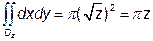 ,
,
оскільки він дорівнює площі круга. Отже,
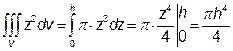 .
.
Зауваження. Якщо область V – прямокутний паралелепіпед 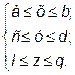 то формула (4) приймає вигляд:
то формула (4) приймає вигляд:
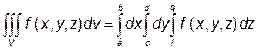 . (8)
. (8)
Якщо підінтегральна функція 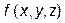 неперервна в області V, то у формулі (8) змінні інтегрування х, у, z можна міняти місцями:
неперервна в області V, то у формулі (8) змінні інтегрування х, у, z можна міняти місцями:
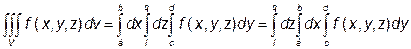
Якщо підінтегральна функція є добутком трьох функцій  , то трикратний інтеграл правої частини рівності (8) буде дорівнювати добутку трьох відповідних визначених інтегралів.
, то трикратний інтеграл правої частини рівності (8) буде дорівнювати добутку трьох відповідних визначених інтегралів.
Приклад 7. Обчислити інтеграл 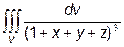 , якщо область V обмежена поверхнями
, якщо область V обмежена поверхнями  ,
, 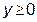 ,
,  , х + у + z = 3.
, х + у + z = 3.
Розв’язання. Область інтегрування V зобразимо на мал. 7. Визначимо аналітичний опис заданої області V. Для визначення меж змінної z проведемо через область V пряму, яка паралельна осі Oz. Тоді одержимо:  .
.
Для опису області D виберемо сталі межі зміни х: 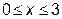 . Тоді y буде змінюватись в межах:
. Тоді y буде змінюватись в межах: 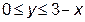 .
.

|
Мал.7
За формулою (4) перейдемо від заданого потрійного інтеграла до трикратного інтеграла:
Отже, область V має аналітичний опис:
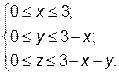
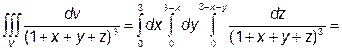
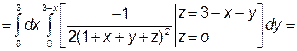
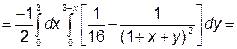 =
= 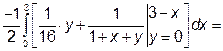
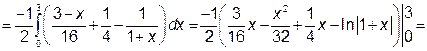
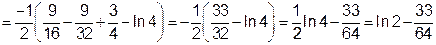 .
.
Приклад 8. Обчислити об’єм області, обмеженої еліпсоїдом
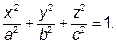
Розв’язання. Згідно властивості 6 інтеграла по області шуканий об’єм v області V знайдемо за формулою:
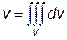 .
.
Область V обмежена знизу поверхнею 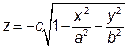 ,
,
а зверху поверхнею 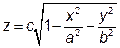 .
.
Область V проектується на площину хОу в область D, яка обмежена еліпсом  .
.
Тому область V аналітично описується нерівностями:
.
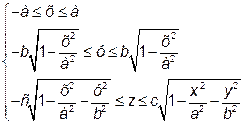
За формулою (4) одержимо:

Для обчислення внутрішнього інтеграла зробимо підстановку
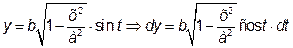
При такій підстановці t змінюється від 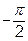 до
до 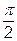 . Одержимо:
. Одержимо:
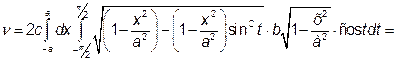
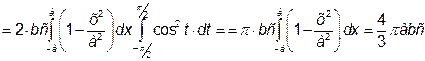 .
.
Отже, об’єм еліпсоїда 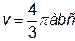 .
.
Якщо а = b = с, то одержимо об’єм кулі  .
.
Приклад 9. Обчислити масу області V, якщо густина розподілу маси 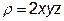 , а область V є циліндром
, а область V є циліндром 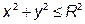 ,
, 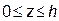 .
.
Розв’язання. Згідно пункту 12.1.4 шукану масу m знайдемо за формулою:
 .
.
Будемо шукати масу чверті циліндра і одержаний результат помножимо на 4. Тоді
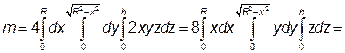
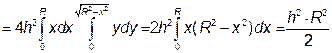 .
.
Основні поняття
Інтеграли по області  називають невластивими, якщо область інтегрування D необмежена або підінтегральна функція
називають невластивими, якщо область інтегрування D необмежена або підінтегральна функція 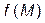 необмежена в деяких точках М області інтегрування. Невластиві інтеграли по області можуть бути збіжними або розбіжними.
необмежена в деяких точках М області інтегрування. Невластиві інтеграли по області можуть бути збіжними або розбіжними.
Випадок нескінченної області. Якщо функція 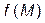 неперервна в нескінченій області D, то розглядають
неперервна в нескінченій області D, то розглядають
 , (1)
, (1)
де Dn – обмежена область така, що  і
і  , тобто Dn розширюється за довільним законом і містить довільну точку область D.
, тобто Dn розширюється за довільним законом і містить довільну точку область D.
Якщо границя правої частини рівності (1) існує і не залежить від вибору області Dn, то відповідний невластивий інтеграл по області D називається збіжним. Якщо ця границя не існує або дорівнює нескінченності, то невластивий інтеграл називають розбіжним.
Якщо підінтегральна функція 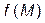 невід’ємна в області D, то для збіжності невластивого інтеграла необхідно і достатньо, щоб границя правої частини рівності (1) існувала хоча би для одного вибору областей Dn.
невід’ємна в області D, то для збіжності невластивого інтеграла необхідно і достатньо, щоб границя правої частини рівності (1) існувала хоча би для одного вибору областей Dn.
Випадок розривної (необмеженої) функції. Якщо функція 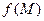 неперервна в замкненій обмеженої області D за виключенням точки М 0, то розглядають
неперервна в замкненій обмеженої області D за виключенням точки М 0, то розглядають
 , (2)
, (2)
де 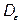 – область, яка одержується із області D шляхом видалення області діаметром e, яка містить точку М 0.
– область, яка одержується із області D шляхом видалення області діаметром e, яка містить точку М 0.
Якщо границя правої частини (2) існує і не залежить від виду видалених областей діаметром  , то відповідний невластивий інтеграл називається збіжним, в протилежному випадку – розбіжним.
, то відповідний невластивий інтеграл називається збіжним, в протилежному випадку – розбіжним.
Якщо  , то границя в (2) не залежить від виду видаленої області. В цьому випадку найчастіше видаляють окіл радіуса e точки М0.
, то границя в (2) не залежить від виду видаленої області. В цьому випадку найчастіше видаляють окіл радіуса e точки М0.
Якщо в області інтегрування підінтегральна функція має розриви другого роду (стає необмеженою) на деякій лінії L або поверхні S, то ця особливість видаляється із області інтегрування, а потім видалена частина стягується до особливості.
Приклад 11. Дослідити збіжність інтеграла  , де область D – площина хОу.
, де область D – площина хОу.
Розв’язання. Заданий інтеграл є невластивим подвійним інтегралом по необмеженій області D, підінтегральна функція невід’ємна. Позначимо через DR – круг радіуса R з центром в початку координат. Тоді рівність (1) прийме вигляд:
 .
.
Обчислимо подвійний інтеграл по області DR переходом до полярної системи координат:
 .
.
Отже,  .
.
Відповідь: невластивий інтеграл – збіжний і дорівнює  .
.
Приклад 12. Дослідити збіжність інтеграла
 .
.
Розв’язання. Задано невластивий подвійний інтеграл по обмеженій області від функції, яка необмежена на колі
х 2 + у 2 = 4 і невід’ємна.
Позначимо через 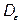 круг радіуса R = 2 –
круг радіуса R = 2 –  з центром в початку координат. Тоді за формулою (2) одержимо:
з центром в початку координат. Тоді за формулою (2) одержимо:
 .
.
Обчислимо подвійний інтервал по області 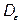 переходом до полярних координат:
переходом до полярних координат:


Заданий інтеграл дорівнює
 ,
,
тому він збіжний.
Зауваження:
1. Якщо підінтегральна функція  і
і 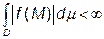 , то невластивий інтеграл по області
, то невластивий інтеграл по області  називають абсолютно збіжним.
називають абсолютно збіжним.
Для обчислення абсолютно збіжного інтеграла по області межі інтегралів можна визначати у будь-якій системі координат.
Якщо інтеграл по області абсолютно не збігається, то заміна змінних і переставлення порядку інтегрування потребують спеціального дослідження.
2. При дослідженні збіжності невластивих інтегралів по області часто застосовують порівняльні ознаки. Наприклад, якщо D є площиною, то для збіжності інтеграла  істотно лише поведінка
істотно лише поведінка 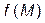 для великих
для великих  , тому потрібно використовувати інтеграл
, тому потрібно використовувати інтеграл  , який збігається р > 2 і розбігається при р < 2.
, який збігається р > 2 і розбігається при р < 2.
Аналогічно в тривимірному просторі інтеграл від  на нескінченності збігається лише при р > 3.
на нескінченності збігається лише при р > 3.
При досліджені невластивих інтегралів по області від функції, яка необмежена в ізольованій точці М 0 області D часто використовують порівняння з інтегралами 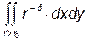 на площині та
на площині та  в просторі.
в просторі.
Перший із вказаних інтегралів збігається при р < 2, а другий – при р < 3.
Якщо особливості підінтегральної функції не ізольовані, то умову збіжності часто вдається одержати шляхом вибору такої системи координат, в якій координатні лінії проходять вздовж особливості.
 |
1.Обчислити інтеграли:
а)

 .
. міру частини Dі, діаметром di, а через
міру частини Dі, діаметром di, а через  – максимальний діаметр частин D 1, D 2,..., Dn, тобто
– максимальний діаметр частин D 1, D 2,..., Dn, тобто  .
.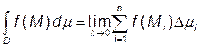 (1)
(1) .
. .
.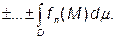
 у довільній точці
у довільній точці  , то виконується нерівність
, то виконується нерівність .
. .
. , то інтеграл від такої функції по області D дорівнює мірі області
, то інтеграл від такої функції по області D дорівнює мірі області . (2)
. (2) , то
, то .
.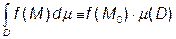 .
. .
. пишуть
пишуть 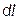 . Якщо дуга АВ – плоска і лежить в площині хОу, тоді точка М дуги АВ має координати (х, у), тому
. Якщо дуга АВ – плоска і лежить в площині хОу, тоді точка М дуги АВ має координати (х, у), тому (3)
(3) , тому
, тому (4)
(4)
 . (5)
. (5)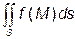 .
. пишуть
пишуть  . Два знаки інтеграла вказують, що інтегрування ведеться по двовимірній області. Якщо поверхня S не плоска, тоді
. Два знаки інтеграла вказують, що інтегрування ведеться по двовимірній області. Якщо поверхня S не плоска, тоді  і тому
і тому (6)
(6) ,
, 
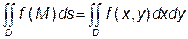 (7)
(7) .
. , то існують і такі позначення потрійного інтеграла:
, то існують і такі позначення потрійного інтеграла: . (8)
. (8) ,
,  ,
,  . (9)
. (9) – нормаль до поверхні S.
– нормаль до поверхні S. .
.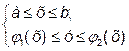 (1)
(1) . (2)
. (2) (3)
(3) (4)
(4) , (5)
, (5)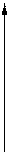





 d
d








 D
D  D
D 



 a 0 b x 0 x
a 0 b x 0 x

 Y
Y

 .
.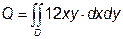 .
. , яка проходить паралельно осі Ох через точку перетину заданої прямої і параболи
, яка проходить паралельно осі Ох через точку перетину заданої прямої і параболи  . Використовуючи властивості інтеграла по області отримаємо:
. Використовуючи властивості інтеграла по області отримаємо:




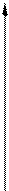





 4x+4y-3=0
4x+4y-3=0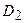


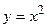 x
x
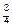

 .
.

 (од. зар.).
(од. зар.).