
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы о пределах последовательности.Содержание книги Поиск на нашем сайте Теорема 1: (необходимый признак числовой последовательности): если последовательность сходится, то она ограничена., если последовательность неограниченна, то она расходится. Теорема Вейерштрасса: сформируем достаточный признак числовой последовательности: всякая ограниченная монотонная последовательность имеет предел. Теорема: если две последовательности {xn}и {yn} сходятся, т.е. имеют конечные пределы, то сходятся также сумма, разность, произведение, частное этих последовательностей, т.е.: Теорема: если Доказательство:
Предел функции. Сформулируем два, эквивалентных между собой, определения предела функции в точке: Определение (по Коши): число А называется пределом функции в точке х0, если для любого положительного Коротко это определение:
Определение (по Гейне): Число А называется пределом функции Односторонние пределы: Предел слева записывают так: Аналогично определяется предел функции справа:
Пределы функции слева и справа называются односторонними пределами. Предел функции при Число А называется пределом функции при
Бесконечно малые и бесконечно большие функции. Функция
Функция
Всякая бесконечно большая функция в окрестности точки х0 является неограниченной в этой окрестности. Бесконечно малая функция: Теорема: алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция. Док-во:
Теорема: произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая. Док-во:
Следствие: так как всякая б.м.ф. ограничена, то из теоремы вытекает произведение двух б.м.ф. есть функция бесконечно малая. Следствие: произведение б.м.ф. на число есть функция бесконечно малая. Теорема: частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая. Док-во:
Теорема: если функция - бесконечно малая, то обратная ей функция – бесконечно большая и наоборот. Док-во:
Односторонние пределы.
Предел слева записывают так: Аналогично определяется предел функции справа:
Пределы функции слева и справа называются односторонними пределами.
Сравнение бесконечно малых. Две б.м.ф. сравниваются между собой с помощью их отношения: 1. если 2. если 3. если 4. если Таковы же правила сравнения б.м.ф. при Эквивалентные бесконечно малые:
Теоремы о пределах. Теорема: если существует Теорема: если 1) 2) 3) Примечание 1: 1-е и 2-е свойства распространяются на любое конечное число слагаемых или сомножителей, однако число слагаемых и сомножителей не может быть Примечание 2: Теорема: если Следствие: если Теорема: если Теорема (о сжатой переменной): если Теорема (о пределе сложной функции): Пусть: х0,
Сама теорема: Если
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.009 с.) |

 =>
=>  и тд.
и тд.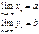 и начиная с некоторого номера выполняется неравенство xn
и начиная с некоторого номера выполняется неравенство xn  yn, то а
yn, то а  следует, что для любого
следует, что для любого  >0 найдется такое натуральное число N(
>0 найдется такое натуральное число N( и
и  т.е.
т.е. и
и  . Возьмем
. Возьмем 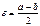 . Тогда:
. Тогда: 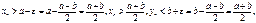 отсюда следует, что xn>yn, это противоречит условию xn
отсюда следует, что xn>yn, это противоречит условию xn  , что для всех х
, что для всех х  х0, удовлетворяющих неравенству
х0, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  .
. .
. в точке х0, если для любой последовательности допустимых значений аргумента хn, сходящейся к х0, последовательность соответствующих значений функции
в точке х0, если для любой последовательности допустимых значений аргумента хn, сходящейся к х0, последовательность соответствующих значений функции  ,
, 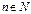 , сходится к числу А.
, сходится к числу А. слева в точке x0, если для любого число
слева в точке x0, если для любого число  >0 существует число
>0 существует число  выполняется неравенство
выполняется неравенство  .
.
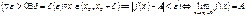 .
. :
: , если для любого положительного числа
, если для любого положительного числа  выполняется неравенство
выполняется неравенство  . Коротко:
. Коротко:
 называется бесконечно большой при
называется бесконечно большой при 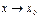 , если для любого числа M>0 существует число
, если для любого числа M>0 существует число  , выполняется неравенство
, выполняется неравенство  . Записывают
. Записывают  . Коротко:
. Коротко:
 называется бесконечно большой при
называется бесконечно большой при  , если для любого числа M>0 найдется такое число N=N (М)>0, что для всех х, удовлетворяющих неравенству
, если для любого числа M>0 найдется такое число N=N (М)>0, что для всех х, удовлетворяющих неравенству 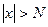 , выполняется неравенство
, выполняется неравенство  . Коротко:
. Коротко:
 , если
, если  : для любого числа
: для любого числа  , выполняется неравенство
, выполняется неравенство  .
. слева в точке x0, если для любого число
слева в точке x0, если для любого число  выполняется неравенство
выполняется неравенство  .
.
 .
. , то
, то  и
и 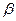 называются бесконечно малыми одного порядка.
называются бесконечно малыми одного порядка. то
то  называется бесконечно малой более высокого порядка, чем
называется бесконечно малой более высокого порядка, чем  .
.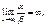 то
то  называется бесконечно малой более низкого порядка, чем
называется бесконечно малой более низкого порядка, чем  .
.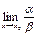 не существует, то
не существует, то  и
и  называются несравнимыми бесконечно малыми.
называются несравнимыми бесконечно малыми. и
и  .
.
 ,
, 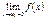 и
и  и они равны между собой, то существует
и они равны между собой, то существует 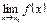 =
= 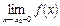
 .
. ,
,  , то =>
, то =>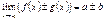
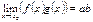

 .
.
 , то функция g(x) = f(x) – a является б.м. при
, то функция g(x) = f(x) – a является б.м. при  .
. => в окрестности т. х0 g(x) + а = f(x), где g(x)- б.м. при
=> в окрестности т. х0 g(x) + а = f(x), где g(x)- б.м. при  и существуют конечные пределы, когда
и существуют конечные пределы, когда  ,
,  =>
=>  .
. и существуют конечные пределы
и существуют конечные пределы 
 => существует:
=> существует:  .
. , U=f(x),
, U=f(x),  .
.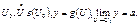
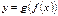 и существуют конечные пределы
и существуют конечные пределы 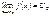 и
и  , то
, то 



