
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первый замечательный предел.Содержание книги Поиск на нашем сайте
При вычислении пределов выражений, содержащих тригонометрические функции, часто используют предел Читается: предел отноешния синуса к его аргументу равен единице, когда аргумент стремится к нулю. Доказательство: Возьмем круг радиуса 1, обозначим радианную меру угла МОВ через х. пусть 0<x< Так как А если x<0 => Второй замечательный предел. Как известно, предел числовой последовательности
Непрерывность функции в точке. Пусть функция f(x) определена в некоторой окрестности O(x0) точки x0 (включая саму точку x0). Функция f(x) называется непрерывной в точке x0, если существует
Необходимое и достаточное условие непрерывности функции в точке: Функция y = f(x) непрерывна в точке х0 тогда и только тогда, когда
Замечание. Условие можно трактовать как второе определение непрерывности функции в точке. Оба определения эквивалентны. Пусть функция f(x) определена в полуинтервале [x0, x0 + δ). Функция f(x) называется непрерывной справа в точке x0, если существует односторонний предел Пусть функция f(x) определена в полуинтервале (x0 − δ, x0]. Функция f(x) называется непрерывной слева в точке x0, если существует односторонний предел
Непрерывность суммы, произведения и частного двух непрерывных функций: Теорема 1. Если функции f(x) и g(x) непрерывны в точке х0, то в этой точке непрерывны f(x) ± g(x),
f(x) · g(x),
Классификация точек разрыва. Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.
Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
Если односторонний предел
Если односторонний предел
Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Если значения на концах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке, либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию в точке, то полученная изменённая функция будет уже непрерывна в точке и разрыв в точке исчезнет; отсюда и название такого разрыва -- устранимый.
|
|||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.208.224 (0.006 с.) |

 называемый первым замечательным пределом.
называемый первым замечательным пределом.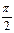 . На рисунке
. На рисунке  , дуга МВ численно равна центральному углу х,
, дуга МВ численно равна центральному углу х, 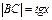 . Очевидно, имеем
. Очевидно, имеем  . На основании соответствующих формул геометрии получаем
. На основании соответствующих формул геометрии получаем  . Разделим неравенство на
. Разделим неравенство на  >0, Получим 1<
>0, Получим 1< 
 , то по признаку (о пределе промежуточной функции) существования пределов
, то по признаку (о пределе промежуточной функции) существования пределов  .
. , где –x>0 =>
, где –x>0 => 
 , имеет предел равный e.
, имеет предел равный e.  . 1.Пусть
. 1.Пусть  . Каждое значение x заключено между двумя положительными целыми числами:
. Каждое значение x заключено между двумя положительными целыми числами:  , где n=[x] – это целая часть x. Отсюда следует
, где n=[x] – это целая часть x. Отсюда следует  , поэтому
, поэтому  . Если
. Если  , то
, то  . Поэтому:
. Поэтому:  ,
, . По признаку существования пределов:
. По признаку существования пределов:  . 2. Пусть
. 2. Пусть  . Сделаем подстановку –x=t, тогда
. Сделаем подстановку –x=t, тогда  =
=  .
.  и
и  называются вторым замечательным пределом. Они широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием e. Функция
называются вторым замечательным пределом. Они широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием e. Функция  называется экспоненциональной, употребляется также обозначение
называется экспоненциональной, употребляется также обозначение 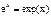 .
. , равный значению функции f(x) в этой точке:
, равный значению функции f(x) в этой точке:  =f(x0).
=f(x0).


 , (g(x0) ≠ 0).
, (g(x0) ≠ 0). , то функция называется непрерывной справа.
, то функция называется непрерывной справа.
 , то функция называется непрерывной слева.
, то функция называется непрерывной слева.


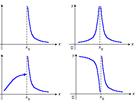
 точка устранимого разрыва – когда пределы слева и справа существуют и равны между собой, но не совпадают со значением функции в точке х0 или функция не определена в точке х0.
точка устранимого разрыва – когда пределы слева и справа существуют и равны между собой, но не совпадают со значением функции в точке х0 или функция не определена в точке х0.


