
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовая последовательность и ее пределСодержание книги Поиск на нашем сайте
КОЛОКВИУМ 1 §1. Понятие и способы задания функций. Основные свойства функции. Сложная и обратная функции. О.1. Пусть даны два непустых множества При этом Функция может быть задана тремя основными способами: аналитически, таблично или графически. Например: 1) функция
2) функция
Рассмотрим основные свойства функций. 1. Четность и нечетность. Функция График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат. 2. Монотонность. Функция Т.е. если Если Функции возрастающие, убывающие, неубывающие, невозрастающие называются монотонными функциями. Функции возрастающие, убывающие, называются строго монотонными функциями. 3. Ограниченность. Функция Число Например, функция 4. Периодичность. Функция Если За основной период берут наименьшее положительное число Т, удовлетворяющее равенству Если функции 5. Явные и неявные функции. Функция называется явной, если она задана формулой, в которой правая часть не содержит зависимой переменной; например, функция у=х2 +5х + 1.Функция
Обратную функцию обозначают так же в виде Таким образом, функция
7. Сложная функция. Пусть функция Переменную Например,
§2. Основные элементарные функции, классификация функций. Преобразование графиков функций О.1. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными. К основным элементарным относятся следующие функции: степенная функция у=хα, α Например, функции Примерами неэлементарных функций являются функции у= | х |, у= [ х ]. Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные). Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий. К числу алгебраических функций относятся: 1) целая рациональная функция (многочлен или полином): 2) дробно-рациональная функция — отношение двух многочленов; 3) иррациональная функция (если в составе операций над аргументом имеется извлечение корня). Любая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические. Рассмотрим методику построения графиков функций, основанную на применении некоторых правил построения по уже известным графикам функций. Правило 1. Чтобы получить график функции Правило 2. Чтобы получить график функции Правило 3. Чтобы получить график функции Правило 4. Чтобы получить график функции Правило 5. Чтобы построить график функции При этом от умножения всех значений функции Правило 6. Чтобы построить график функции При этом от деления всех значений аргумента функции Правило 7. Чтобы получить график функции Правило 8. Чтобы получить график функции у= f(|х|) из графика функции
Предел функции Пусть функция О.1. (по Коши). Число
Обозначается Смысл определения предела функции О.2. (по Гейне). Число Определение предела не требует существования функции в самой точке В определении предела функции считается, что Бывают случаи, когда способ приближения аргумента О.3. Число Предел слева записывают так: Аналогично определяется предел функции справа: Пример. Найти правосторонний предел и левосторонний предел функции Решение: Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует О.4. Число Примеры функций имеющих пределы: 1. 2. 3. 4. 5. 6. Примеры. 1. Последовательность {п} является бесконечно большой. 2. Последовательность { Теорема 1. Если {хп} - бесконечно большая последовательность и все ее члены отличны от нуля, хп ≠0, то последовательность {αп}= Сформулируем основные свойства бесконечно малых последовательностей в виде теорем. Теорема 2. Сумма и разность двух бесконечно малых последовательностей есть бесконечно малые последовательности. Пример 2. Последовательность с общим членом Следствие. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. Теорема 3. Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность. Следствие. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. Замечание. Частное двух бесконечно малых последовательностей может быть любой последовательностью и может не иметь смысла. Например, если Теорема 4. Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность. Пример 3. Последовательность Следствие. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность. Определение. Функция f(x) называется бесконечно большой при
Записывают: Например, функция Если f(x) стремится к бесконечности при Определение. Функция f(x), заданная на всей числовой прямой, называется бесконечно большой при
Например, функция у=2х есть бесконечно большая функция при Свойства бесконечно больших функций: 1. Произведение б.б.ф. на функцию, предел которой отличен от нуля, есть б.б.ф. 2. Сумма б.б.ф. и ограниченной функции есть б.б.ф. 3. Частное от деления б.б.ф. на функцию, имеющую предел, есть б.б.ф. Например, если функция f(x)=tgx есть б.б.ф. при f(x) φ(х)=(4х-3) tgx; f(x) + ψ(х)= tgx + sinx;
Определение. Функция f(x) называется бесконечно малой при
По определению предела функции равенство (1) означает: для любого, даже сколь угодно малого положительного числа
Теорема. Для выполнения равенства Аналогично определяется б.м.ф. при Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами α, β и т.д. Например, у=х2 при х→0; у=х-2 при х→2; у=sinx при х→πк, Свойства бесконечно малых функций: 1. Сумма конечного числа бесконечно малых функций есть величина бесконечно малая; 2. Произведение конечного числа бесконечно малых функций, а также бесконечно малой функции на ограниченную функция, есть величина бесконечно малая; 3. Частное от деления бесконечно малой функции на функцию, предел которой не равен нолю, если величина бесконечно малая. Рассмотрим последнее свойство при 1). Если Пример. При х→2 функция (х — 2)3 бесконечно малая более высокого порядка, чем (х -2), так как 2). Если Пример. При х→0 функции 5х2 и х2 являются бесконечно малыми одного порядка, так как
3). Если Эквивалентные бесконечно малые при 1. 2. 3. 4. 5. 6. 7. 8. 9. Теорема. Если существует предел отношения двух бесконечно малых α и β, то он равен пределу отношения соответствующих им эквивалентных бесконечно малых. Пример:
Определить порядок малости можно по следующему правилу: 4). Если Пример: Определить порядок малости
Таким образом, бесконечно малая Связь между бесконечно малыми и бесконечно большими функциями: функция обратная бесконечно малой является бесконечно большой (и наоборот), т.е. если Пример.
Замечание. В общем случае справедливы равенства Предел последовательности с общим членом
Замечание. Если обозначить Доказательство первого и второго замечательного предела самостоятельно. Пример. Предел КОЛОКВИУМ 2 ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ Производная функции 1. Задачи, приводящие к понятию производной. 2. Определение производной. Общее правило дифференцирования. - 1 - Понятие производной является одним из основных математических понятий. Производная широко используется при решении многих задач. 1. | ||
|
| Поделиться: |

 и
и 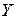 . Соответствие (закон)
. Соответствие (закон)  , которое каждому элементу
, которое каждому элементу  сопоставляет один и только один элемент
сопоставляет один и только один элемент  , называется функцией и записывается
, называется функцией и записывается  или
или 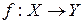 .
. является независимой переменной или аргументом,
является независимой переменной или аргументом,  - зависимой переменной или значением функции, множество
- зависимой переменной или значением функции, множество  функции, множество
функции, множество 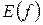 функции, а буква f обозначает закон соответствия.
функции, а буква f обозначает закон соответствия. (антье) – целая часть, где n – наибольшее из целых чисел не превосходящее аргумента
(антье) – целая часть, где n – наибольшее из целых чисел не превосходящее аргумента 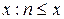 .
.
 - дробная часть числа:
- дробная часть числа:  .
.
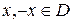
 и нечетной, если
и нечетной, если  . Иначе функция
. Иначе функция  и
и 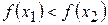 , то функция возрастает; если
, то функция возрастает; если  , то функция убывает.
, то функция убывает. то функция называется неубывающей, если
то функция называется неубывающей, если  , то функция называется невозрастающей.
, то функция называется невозрастающей. , определенная на множестве
, определенная на множестве  называется ограниченной сверху (снизу) на этом множестве, если существует число
называется ограниченной сверху (снизу) на этом множестве, если существует число  , такоечто для всех
, такоечто для всех 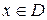 выполняется неравенство
выполняется неравенство 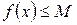
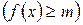 . Иначе функция называется неограниченной.
. Иначе функция называется неограниченной. ограничена на всей числовой оси, так как
ограничена на всей числовой оси, так как  для любого
для любого  .
. , что при любом
, что при любом  и
и 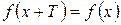 . При этом число
. При этом число 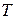 называется периодом функции.
называется периодом функции. , где
, где 
 и
и  периодические с периодами
периодические с периодами  и
и 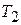 соответственно, то периодом их суммы, произведения, разности и частного является число
соответственно, то периодом их суммы, произведения, разности и частного является число  , не разрешенным относительно зависимой переменной. Например, функция у(у>0), заданная уравнением х5 + у2 - х =0.
, не разрешенным относительно зависимой переменной. Например, функция у(у>0), заданная уравнением х5 + у2 - х =0. 6. Обратная функция. Пусть
6. Обратная функция. Пусть  . Тогда полученная функция
. Тогда полученная функция  , определенная на множестве
, определенная на множестве  . Например, для функции у=ах обратной будет функция х=logaу или (в обычных обозначениях зависимой и независимой переменных) у= loga x.
. Например, для функции у=ах обратной будет функция х=logaу или (в обычных обозначениях зависимой и независимой переменных) у= loga x. Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов. есть функция от переменной
есть функция от переменной  , определенной на множестве
, определенной на множестве  с областью значений
с областью значений  от переменной
от переменной  называется сложной функцией.
называется сложной функцией. — сложная функция, так как ее можно представить в виде
— сложная функция, так как ее можно представить в виде  , где
, где 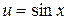 .
. R; показательная функция у=ах, а › 0, а ≠1; логарифмическая функция y=logax, а › 0, а ≠1; тригонометрические формулы и обратные тригонометрические формулы.
R; показательная функция у=ах, а › 0, а ≠1; логарифмическая функция y=logax, а › 0, а ≠1; тригонометрические формулы и обратные тригонометрические формулы. ;
;  является элементарной, так как здесь число операций сложения, вычитания, умножения, деления и образования сложной функции конечно.
является элементарной, так как здесь число операций сложения, вычитания, умножения, деления и образования сложной функции конечно. ;
;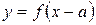 из графика функции
из графика функции  на
на  вправо, если
вправо, если  , или на
, или на  влево, если
влево, если  .
. из графика функции
из графика функции  на
на  вверх, если
вверх, если  , или на
, или на  вниз, если
вниз, если  .
. из графика функции
из графика функции 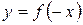 из графика функции
из графика функции  , нужно значение ординаты графика функции
, нужно значение ординаты графика функции  , а абсциссу оставить без изменения.
, а абсциссу оставить без изменения. ординаты графика функции увеличатся в
ординаты графика функции увеличатся в  ординаты графика функции уменьшаются в
ординаты графика функции уменьшаются в 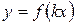 , нужно значение
, нужно значение  из графика функции
из графика функции  и отразить его зеркально относительно оси
и отразить его зеркально относительно оси  , кроме, может быть, самой точки
, кроме, может быть, самой точки 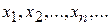 сходящуюся к
сходящуюся к  , и можно говорить о существовании ее предела.
, и можно говорить о существовании ее предела. называется пределом функции
называется пределом функции 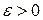 , найдется такое число
, найдется такое число  (
( ), что для всех
), что для всех  и удовлетворяющих условию
и удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство
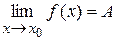 .
. ), если для любой последовательности допустимых значений аргумента
), если для любой последовательности допустимых значений аргумента  , сходящейся к
, сходящейся к 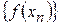 сходится к числу
сходится к числу  , мы предполагаем, что
, мы предполагаем, что  , но не достигает значения
, но не достигает значения  называется пределом функции
называется пределом функции 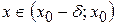 , выполняется неравенство
, выполняется неравенство 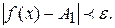
 .
. .
. .
.

 и
и 
 , то существуют и оба односторонних предела, причем
, то существуют и оба односторонних предела, причем  . Если же
. Если же 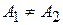 , то
, то  не существует.
не существует. , если для любого числа
, если для любого числа  (
(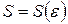 ), что для всех
), что для всех  , выполняется неравенство
, выполняется неравенство  .
. .
. .
. .
. .
.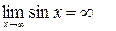 не существует.
не существует. } является бесконечно малой.
} является бесконечно малой. - бесконечно малая, и, обратно, если {αп} бесконечно малая последовательность, αп≠0, то последовательность {хп}=
- бесконечно малая, и, обратно, если {αп} бесконечно малая последовательность, αп≠0, то последовательность {хп}=  бесконечно большая.
бесконечно большая. бесконечно малая, т.к.
бесконечно малая, т.к. 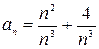 т.е заданная последовательность является суммой бесконечно малых последовательностей
т.е заданная последовательность является суммой бесконечно малых последовательностей  и
и  и поэтому является бесконечно малой.
и поэтому является бесконечно малой.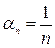 ,
,  , то все элементы последовательности
, то все элементы последовательности  равны 1 и данная последовательность является ограниченной. Если
равны 1 и данная последовательность является ограниченной. Если  , то последовательность
, то последовательность  , а
, а  равны нулю, то последовательность
равны нулю, то последовательность 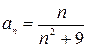 бесконечно малая, т.к.
бесконечно малая, т.к.  и последовательность {
и последовательность {  - ограничена, т.к.
- ограничена, т.к.  , если для любого, даже сколь угодно большого положительного числа
, если для любого, даже сколь угодно большого положительного числа  , найдется такое положительное число
, найдется такое положительное число  (зависящее от М, δ=δ(М)), что для всех х, не равных х0 и удовлетворяющих условию
(зависящее от М, δ=δ(М)), что для всех х, не равных х0 и удовлетворяющих условию 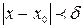 , выполняется неравенство
, выполняется неравенство
 или
или  при
при  есть бесконечно большая функция при
есть бесконечно большая функция при  ; функция
; функция  при
при  .
.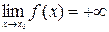 , если лишь отрицательные значения, то
, если лишь отрицательные значения, то 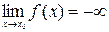 .
. , если для любого положительного числа
, если для любого положительного числа 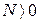 (зависящее от М, N=N(М)), что при всех х, удовлетворяющих условию
(зависящее от М, N=N(М)), что при всех х, удовлетворяющих условию 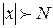 , выполняется неравенство
, выполняется неравенство является бесконечно большой функцией при
является бесконечно большой функцией при  есть бесконечно большие функции при
есть бесконечно большие функции при  . (1)
. (1) , найдется такое положительное число
, найдется такое положительное число 
 необходимо и достаточно, чтобы функция
необходимо и достаточно, чтобы функция  была бесконечно малой при
была бесконечно малой при 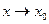 . При этом функция может быть представлена в виде
. При этом функция может быть представлена в виде  .
. ,
,  во всех случаях f(x)
во всех случаях f(x)  0.
0. - бесконечно малые функции.
- бесконечно малые функции. и
и  являются бесконечно малыми (Сравнение бесконечно малых функций):
являются бесконечно малыми (Сравнение бесконечно малых функций): , то
, то  .
.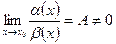 , то
, то  .
. ,то
,то  :
:







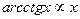



 , то
, то  -го порядка малости относительно от
-го порядка малости относительно от  , относительно бесконечно малой
, относительно бесконечно малой  .
.






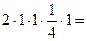
 .
. - бесконечно малая функция, то
- бесконечно малая функция, то  - бесконечно большая.
- бесконечно большая.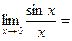

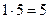
 ,
,  и
и 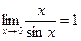
 при
при 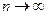 называется вторым замечательным пределом и равен числу
называется вторым замечательным пределом и равен числу  , т.е.
, т.е.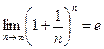 .
. , то второй замечательный предел можно записать в виде
, то второй замечательный предел можно записать в виде  .
.
 .
.


