
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о производительности трудаСодержание книги Поиск на нашем сайте Пусть функция u=u(t) выражает количество произведенной продукции u за время t и необходимо найти производительность труда в момент времени t0. За период времени от t0 до (t0+Dt) количество произведенной продукции изменится от значения u0=u(t0) до значения u0+Du=u(t0+Dt); тогда средняя производительность труда на этот период времени
- 2 - Определение. Производной функции у=f(х) в точке х0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т.е.
Производная функции также может быть обозначена одним их символов Функция у=f(х), имеющая производную в каждой точке интервала (a;b) называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием. Производная функции у=f(х) может быть найдена по схеме: 1. Дадим аргументу х приращение Dх≠0 и найдем наращенное значение функции у+Dу=f(х+Dх). 2. Находим приращение функции Dу= f(х+Dх)-f(х). 3. Составляем отношение 4. Находим предел этого отношения при Пример. Используя определение найти производную функции у=х3.. Решение. 1) Дадим аргументу х приращение Dх≠0 и найдем наращенное значение функции у+Dу=(х+Dх)3. 2) Находим приращение функции Dу=(х+Dх)3-х3=х3+3х2Dх+3хDх2+Dх3-х3=Dх(3х2+3хDх+Dх2). 3) Составляем отношение 4) Находим предел Теорема. Если функция дифференцируема в некоторой точке, то она непрерывна в ней. Обратная теорема неверна: непрерывная функция может не иметь производной. Правила дифференцирования 1. Правила дифференцирования. 2. Производные сложной и обратной функций. 3. Производные основных элементарных функций, таблица производных. 4. Производные высших порядков.
- 1 - Нахождение производной функции непосредственно по определению часто связано с определенными трудностями. На практике функции дифференцируют с помощью ряда правил и формул. Пусть функции u=u(x) и Теорема 1. Производная суммы (разности) двух функций:
Теорема справедлива для любого конечного числа слагаемых. Теорема 2. Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго:
Следствие 1. Постоянный множитель можно выносить за знак производной: Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, например: Теорема 3. Производная частного двух функций
Следствие 3. Следствие 4. Пример 1. Найти производную функции Решение. Значение производной в точке х=1 есть - 2 - Пусть переменная y есть функция от переменной u, то есть у=f(u), а переменная u в свою очередь есть функция от независимой переменной х, то есть Теорема 4. Если функция
Итак, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. Это правило остается в силе, если промежуточных аргументов несколько. Так, если у=f(u), Пусть y=f(x) и Теорема 5. Если функция y=f(x) строго монотонна на интервале (a;b) и имеет неравную нулю производную
Таким образом, производная обратной функции равна обратной величине производной данной функции. Пример 2. Найти производную функции Решение. Данная функция является сложной. Ее можно представить в виде цепочки простых функций: Пример 3. Пользуясь правилом дифференцирования обратной функции, найти производную Решение. Обратная функция
- 3 - Таблица производных элементарных функций
-4- Производная Если функция Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается Производной n-го порядка (или n-й производной) называется производная от производной (n -1) порядка:
Производные порядка выше первого называются производными высших порядков. Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (y V или y (5) ). Дифференциал функции 1. Понятие дифференциала. 2. Применение дифференциала к приближенным вычислениям. 3. Дифференциалы высших порядков. -1- Пусть функция y=f (x) имеет в точке х отличную от нуля производную Таким образом, приращение функции
Поэтому первое слагаемое Определение. Дифференциалом функции y=f (x) в точке х называется главная линейная относительно ∆х часть приращения функции, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x)):
Дифференциал dy называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т.е. дифференциал функции у = х. Так как у´=х´= 1, то согласно формуле (1), имеем dy=dx=∆x, т.е. дифференциал независимой переменной равен приращению переменной: dx=∆x. Поэтому формулу (1) можно записать так:
Иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной. Из формулы (2) следует равенство Пример 1. Найти дифференциал функции Решение: По формуле
Геометрический смысл дифференциала функции.
Но, согласно геометрическому смыслу производной, - 2 - Как уже известно, приращение Δ у функции y=f(x) в точке х можно представить в виде
причем это равенство тем точнее, чем меньше Δ x. Это равенство позволяет с большей точностью вычислить приближенно приращение любой дифференцируемой функции. Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (2) широко применяется в вычислительной практике. Подставляя в равенство
Формула (3) используется для вычислений приближенных значений функций. Пример 4. Вычислить приближенно arctg 1,05. Решение: Рассмотрим функцию f(x)= arctg x. По формуле (3) имеем:
т.е. Так как x+ Δ x =1.05, то при х= 1 и Δ х =0.05 получаем:
-3- Пусть y=f(x) дифференцируемая функция, а ее аргумент х – независимая переменная. Тогда ее первый дифференциал Дифференциал от дифференциала функции y=f(x) называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается Итак, по определению d2y=d(dy). Найдем выражение второго дифференциала функции y=f(x). Так как dx= Δ x не зависит от х, то при дифференцировании считаем dx постоянным и можно выносить за знак дифференциала.
т.е. Аналогично определяется и находится дифференциал третьего порядка:
И, вообще, дифференциал n -го порядка есть дифференциал от дифференциала (n -1)-го порядка: Отсюда находим, что
т.е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной. Пример 5. Найти d2y, если y=e3x и х – независимая переменная. Решение: Так как
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 . Очевидно, что производительность труда в момент t0 можно определить как предельное значение средней производительности за период времени от t0 до t0+Dt при
. Очевидно, что производительность труда в момент t0 можно определить как предельное значение средней производительности за период времени от t0 до t0+Dt при  , т.е.
, т.е. .
. .
. .
.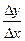 .
. , т.е.
, т.е.  (если этот предел существует).
(если этот предел существует). =
=  (3х2+3хDх+Dх2)= 3х2.
(3х2+3хDх+Dх2)= 3х2. - две дифференцируемые на некотором интервале (a;b) функции.
- две дифференцируемые на некотором интервале (a;b) функции. . (1)
. (1) . (2)
. (2) .
. .
. , если
, если  ≠0 равна дроби, числитель который есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя.
≠0 равна дроби, числитель который есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя. . (3)
. (3) .
. , где с = const.
, где с = const. и вычислить ее значение в точке х=1.
и вычислить ее значение в точке х=1.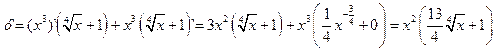
 .
.
 задана сложная функция
задана сложная функция  .
. имеет производную
имеет производную  в точке х, а функция у=f(u) имеет производную
в точке х, а функция у=f(u) имеет производную  в соответствующей точке
в соответствующей точке  в точке х, которая находится по формуле
в точке х, которая находится по формуле . (4)
. (4) ,
,  , то
, то 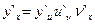 .
. - взаимно-обратные функции.
- взаимно-обратные функции.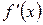 в произвольной точке этого интервала, то обратная ей функция
в произвольной точке этого интервала, то обратная ей функция  в соответствующей точке, определяемую равенством
в соответствующей точке, определяемую равенством или
или 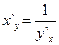 .
.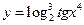 .
. , где
, где  , где
, где  , где
, где  . По правилу дифференцирования сложной функции
. По правилу дифференцирования сложной функции  получаем
получаем 
 .
. имеет производную
имеет производную 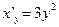 . Следовательно
. Следовательно .
.

































 ,
, 







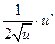
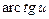



 функции y=f(x) есть также функция от х и называется производной первого порядка.
функции y=f(x) есть также функция от х и называется производной первого порядка. дифференцируема, то ее производная называется производной второго порядка и обозначается
дифференцируема, то ее производная называется производной второго порядка и обозначается  (или
(или  . Итак,
. Итак,  .
.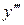 .
. .
. .
. . Тогда по теореме о связи функции, ее предела и бесконечно малой функции, можно записать
. Тогда по теореме о связи функции, ее предела и бесконечно малой функции, можно записать  , где
, где  при
при  , или
, или 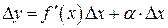 .
.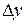 представляет собой сумму двух слагаемых
представляет собой сумму двух слагаемых 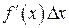 и
и  , являющихся бесконечно малыми при
, являющихся бесконечно малыми при  , т.к.
, т.к.  , а второе слагаемое есть бесконечно малая функция более высокого порядка, чем
, а второе слагаемое есть бесконечно малая функция более высокого порядка, чем  .
. называют главной частью приращения функции ∆у.
называют главной частью приращения функции ∆у. . (1)
. (1)  . (2)
. (2) . Теперь обозначение производной
. Теперь обозначение производной 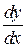 можно рассматривать как отношение дифференциалов dy и dx.
можно рассматривать как отношение дифференциалов dy и dx.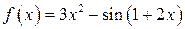 .
. .
. Проведем к графику функции y=f(x) в точке М(х;у) касательную МТ и рассмотрим ординату этой касательной для точки
Проведем к графику функции y=f(x) в точке М(х;у) касательную МТ и рассмотрим ординату этой касательной для точки  . На рис.
. На рис.  . Из треугольника МАВ имеем
. Из треугольника МАВ имеем  , то есть
, то есть  .
. . Поэтому
. Поэтому  Сравнивая полученный результат с формулой (1), получаем dy=AB, т.е. дифференциал функции y=f(x) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение
Сравнивая полученный результат с формулой (1), получаем dy=AB, т.е. дифференциал функции y=f(x) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение  , где
, где 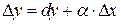 . Отбрасывая бесконечно малую
. Отбрасывая бесконечно малую  более высокого порядка, чем Δ x, получаем приближенное равенство
более высокого порядка, чем Δ x, получаем приближенное равенство (2)
(2) или
или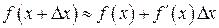 (3)
(3)
 .
.
 .
.
 . (4)
. (4)

 . В частности, при n = 1,2,3 соответственно получаем
. В частности, при n = 1,2,3 соответственно получаем
 то по формуле (4) имеем
то по формуле (4) имеем  .
.


