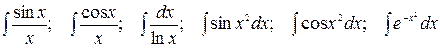Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема №4: Интегрирование тригонометрических функций.Содержание книги
Поиск на нашем сайте
План 1. Универсальная тригонометрическая подстановка. 2. Интегралы типа 3. Использование тригонометрических преобразований.
-1- Функцию с переменными sinx и cosx, над которыми выполняются рациональные действия (сложение, вычитание, умножение, деление) принято обозначать R (sin x; cos x), где R - знак рациональной функции. Вычисление неопределенных интегралов типа Действительно, Из равенства Поэтому, где R1(t)- рациональная функция от t. Обычно этот способ весьма громоздкий, зато он всегда приводит к результату. На практике применяют и другие, более простые подстановки, в зависимости от свойств (и вида) подынтегральной функции. В частности, удобны следующие правила: 1. Если функция R (sin x; cos x) нечетна относительно sin x, т.е. R(-sin x; cos x) = -R (sin x; cos x), то подстановка cos x = t рационализирует интеграл. 2. Если функция R (sin x; cos x) нечетная относительно cos x, т.е. R (sin x; -cos x)=-R (sin x; cos x), то делается подстановка sin x=t. 3. Если функция R (sin x; cos x) четная относительно sin x и cos x, т.е. R (-sin x; -сos x)=R(sin x; cos x), то интеграл рационализируется подстановкой tgx = t. Такая же подстановка применяется, если интеграл имеет вид Пример 1. Найти Решение: Положим
Пример 2: Найти Решение: Так как R(-sinx; -cosx)= Отсюда Поэтому,
- 2- Рассмотрим три вида интегралов. 1. Интегралы вида В данном случае из нечетной степени нужно выделить первую степень функции и подвести ее под знак дифференциала, оставшуюся четную степень функции преобразовать в ту функцию, которая находится под знаком дифференциала по формуле: Пример 3. Найти интеграл
Пример 4. Найти интеграл Решение: =-cosx+ 2. Интегралы вида Пример 5. Найти интеграл Решение: В данном случае используются формулы понижения степени: 3. Интегралы вида
-3- Интегралы типа
Пример 5. Найти интеграл Решение. Тема №5. Интегрирование иррациональных функций
Рассмотрим некоторые типы интегралов, содержащих иррациональные функции. Интегралы типа:
и сделать подстановку При этом первые два интеграла приводятся к табличным, а третий - к сумме двух табличных интегралов. Пример 1. Найти интегралы 1. Решение: Выделим полный квадрат под корнем.
Делаем подстановку
2. Решение: Выделим полный квадрат под корнем в знаменателе.
Делаем подстановку
Интегралы типа Пример 2. Найти Решение: Наименьшее общее кратное чисел 2 и 3 равно 6, данный интеграл является интегралом типа
Сделаем замену переменной еще раз
где С1=С-11 Замечание 1. Многие интегралы можно брать различными методами (например, подстановкой или подведением под знак дифференциала). Интеграл следует брать тем методом, который не создает громоздких вычислений. Рациональный выбор метода интегрирования обусловлен практическим опытом. Замечание 2. При интегрировании функции различными методами получаются на первый взгляд различные ответы (по форме записи, по виду тригонометрической функции и т.д.). В конечном итоге все эти ответы различаются на постоянную величину, что обусловлено самим понятием неопределенного интеграла, и сводятся друг к другу путем математических преобразований. Данная постоянная величина входит в состав постоянной интегрирования С. Некоторые интегралы нельзя взять ни одним из рассмотренных методов интегрирования. Это интегралы вида
и другие. Их называют «неберущимися», но они реально существуют, хотя и представляют собой функции другой природы, не приводящиеся к элементарным функциям.
|
|||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.98.190 (0.007 с.) |

 .
.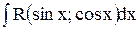 сводится к вычислению интегралов от рациональной функции подстановкой
сводится к вычислению интегралов от рациональной функции подстановкой  , которая называется универсальной.
, которая называется универсальной.
 .
.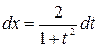 .
.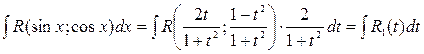 ,
, .
.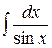 .
. .
.  ,
,  ,
, 
 .
. 

 ,то полагаем tgx=t.
,то полагаем tgx=t. ,
,  и
и  .
.
 , где хотя бы одно из чисел m, n – нечетное.
, где хотя бы одно из чисел m, n – нечетное. .
. .
. =
=  )=
)=  =
=  =
=  .
. .
. =-
=- 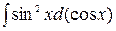 =-
=- 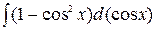 =
=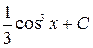 .
. , где m, n – целые неотрицательные четные числа.
, где m, n – целые неотрицательные четные числа. .
.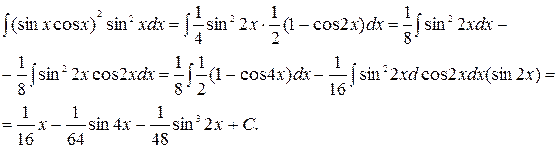
 ,
, 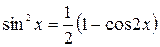 и формула
и формула 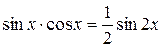 .
. ,
,  ,
,  вычисляются с помощью известных формул тригонометрии.
вычисляются с помощью известных формул тригонометрии.
 .
.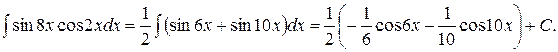
 ,
,  ,
,  - называют неопределенными интегралами от квадратичных иррациональностей. Их можно найти следующим образом: под радикалом выделить полный квадрат
- называют неопределенными интегралами от квадратичных иррациональностей. Их можно найти следующим образом: под радикалом выделить полный квадрат




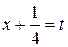 ,
, 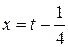 ,
, 
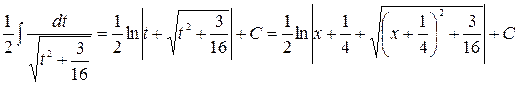 .
.
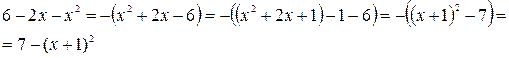
 ,
, 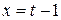 , dx=dt
, dx=dt
 рационализируются заменой переменной
рационализируются заменой переменной 

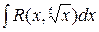 замена переменной
замена переменной  , тогда
, тогда  ,
,  ,
,  ,
, 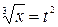 . Следовательно,
. Следовательно,