
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел монотонной последовательности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Последовательность Последовательность Оба этих случая объединяют символом Последовательность Последовательность Теорема о существовании предела монотонной последовательности. 1. Если последовательность Длины и площади в окружности и круге Длиной окружности называется предел последовательности периметров правильных многоугольников, вписанных в данную окружность, при неограниченном увеличении числа сторон. Длина окружности L вычисляется по формуле
Площадью круга называется предел последовательности площадей правильных многоугольников, вписанных в данную окружность, при неограниченном увеличении числа сторон. Площадь круга радиуса
Сектором называется часть круга, ограниченная двумя его радиусами. Площадь сектора вычисляется по формуле
Часть круга, ограниченная хордой и стягиваемой ею дугой, называется сегментом. Сумма бесконечно убывающей геометрической прогрессии равна первому члену этой прогрести, деленному на единицу минус знаменатель этой прогрессии.
Примеры. 1) Сумма геометрической прогрессии
а сумма геометрической прогрессии
Непрерывность функции. Пусть дана функция Определение. Говорят, что функция 1) 2) Сформулируем определение непрерывности в эквивалентной форме. С этой целью обозначим Определение. Говорят, что функция Теорема. Если функции
Задачи, приводящие к понятию производной Понятие производной является одним из основных математических понятий. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости разных процессов.
Скорость прямолинейного движения Если в некоторый момент времени Отношение Средняя скорость зависит от значения Предел средней скорости движения при стремлении к нулю промежутка времени Касательная к кривой Дадим сначала общее определение касательной к кривой. Возьмем на непрерывной кривой L две точки М и М 1. Прямую ММ 1, проходящую через эти точки, называют секущей. Пусть точка М 1, двигаясь вдоль кривой L, неограниченно приближается к точке М. Тогда секущая, поворачиваясь около точки М, стремится к некоторому предельному положению МТ. Касательной к данной кривой в данной точке М называется предельное положение МТ секущей ММ 1, проходящей через точку М, когда вторая точка пересечения М 1неограниченно приближается по кривой к точке М 1.
Рассмотрим теперь график непрерывной кривой у=ƒ(х), имеющий в точке Для этого проведем через точку М и точку М1 графика с абсциссой
При Следовательно, Поэтому угловой коэффициент касательной равен
Определение производной; ее механический и геометрический смысл. Уравнение касательной и нормали к кривой Пусть функция - аргументу
- найдем соответствующее приращение функции: - составим отношение приращения функции к приращению аргумента: - найдем предел этого отношения при Если этот предел существует, то его называют производной функции Производной функции Итак, по определению
Функция Значение производной функции В задаче про скорость прямолинейного движения было получено
Это равенство перепишем в виде Обобщая, можно сказать, что если функция В задаче про касательную к кривой был найден угловой коэффициент касательной
Это равенство перепишем в виде Если точка касания М имеет координаты
Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой. Так как нормаль перпендикулярна касательной, то ее угловой коэффициент
Экономический смысл производной. Использование понятия производной в экономике Производительность труда есть производная объема произведенной продукции по времени. Рассмотрим еще одно понятие, иллюстрирующее экономический смысл производной. Издержки производства Предельные издержки зависят от уровня производства (количества выпускаемой продукции) Предельные величины характеризуют не состояние (как суммарная или средняя величины), а процесс, изменение экономического объекта. Таким образом, производная выступает как скорость изменения некоторого экономического объекта (процесса) по времени или относительного другого исследуемого фактора. Следует учесть, однако, что экономика не всегда позволяет использовать предельные величины в силу неделимости многих объектов экономических расчетов и прерывности (дискретности) экономических показателей во времени (например, годовых, квартальных, месячных и т.д.). Вместе с тем в ряде случаев можно отвлечься от дискретности показателей и эффективно использовать предельные величины.
Производная суммы, разности, произведения и частного функций Нахождение производной функции непосредственно по определению часто связано с определенными трудностями. На практике функции дифференцируют с помощью ряда правил и формул. Пусть функции Теорема. Производная суммы (разности) двух функций равна сумме (разности) производных этих функций:
Теорема справедлива для любого конечного числа слагаемых. Теорема. Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго: Можно показать, что:
Теорема. Производная частного двух функций Производная сложной и обратной функций Пусть Теорема. Если функция По условию
Отсюда, по теореме о связи функции, ее предела и бесконечно малой функции, имеем
где Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Таблица производных Выведенные правила дифференцирования, формулы производных основных элементарных функций запишем в виде таблицы. На практике чаще всего приходится находить производные от сложных функций. Поэтому в приведенной ниже таблице формул дифференцирования аргумент « Правила дифференцирования 1. 2. 3. 4. 5. Таблица производных 1. 3. 5. 7. 9. 11. 13. Для вычисления производных надо знать лишь правила дифференцирования и таблицу производных основных элементарных функций, строго соблюдать эти правила при выполнении упражнений.
Определение. Функция Определение. Функция Теорема. Пусть Определение. Точка Аналогично определяется точка минимума. Точка минимума или максимума называется точкой экстремума. Определение. Точка Теорема. 1) если 2) если 3) если Определение. а) функция б) функция Теорема. Пусть функция a) 6) Cхема исследования функции 1. Область определения 2. Точки пересечения с осями координат. 3. Промежутки знакопостоянства функции. 4. Исследование по первой производной – промежутки убывания, возрастания, экстремумы. Для удобства строится таблица первой производной. 5. Исследование по второй производной – промежутки выпуклости вверх и вниз. Строится таблица второй производной. 6. Специальные свойства – четность, нечетность, периодичность. Если какого-либо или нескольких свойств из перечисленных нет, то о них упоминать не следует; 7. Исследование завершается построением графика функции.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 918; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.100.186 (0.016 с.) |

 называется монотонно возрастающей, если для любого
называется монотонно возрастающей, если для любого  :
:  .
.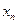 .
.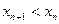 .
. .
. , где
, где  – диаметр окружности, или по формуле
– диаметр окружности, или по формуле , где
, где  – радиус окружности.
– радиус окружности. .
. .
. .
. равна
равна ,
, ,... равна
,... равна .
. с областью определения
с областью определения  и пусть
и пусть  – предельная точка множества
– предельная точка множества  непрерывна в точке
непрерывна в точке  ;
;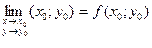 , т.е.
, т.е. 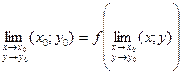 .
. и
и  .
. .
. и
и  непрерывны в точке
непрерывны в точке  , то этим же свойством обладают функции
, то этим же свойством обладают функции  , а если
, а если 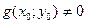 , то и функция
, то и функция  .
. точка занимает положение М, то в момент времени
точка занимает положение М, то в момент времени  (
( – приращение времени) точка займет положение
– приращение времени) точка займет положение  , где
, где  (
( – приращение расстояния). Таким образом, перемещение точки
– приращение расстояния). Таким образом, перемещение точки  за время
за время  .
. – выражает среднюю скорость движения точки за время
– выражает среднюю скорость движения точки за время 
 или
или 


 невертикальную касательную. Найдем ее угловой коэффициент
невертикальную касательную. Найдем ее угловой коэффициент  , где
, где  — угол касательной с осью
— угол касательной с осью  .
. секущую (см. рис. 129). Обозначим через
секущую (см. рис. 129). Обозначим через  — угол между секущей ММ1 и осью Ох. На рисунке видно, что угловой коэффициент секущей равен
— угол между секущей ММ1 и осью Ох. На рисунке видно, что угловой коэффициент секущей равен
 в силу непрерывности функции приращение
в силу непрерывности функции приращение 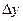 тоже стремится к нулю; поэтому точка М1 неограниченно приближается по кривой к точке М, а секущая ММ1, поворачиваясь около точки М, переходите касательную. Угол
тоже стремится к нулю; поэтому точка М1 неограниченно приближается по кривой к точке М, а секущая ММ1, поворачиваясь около точки М, переходите касательную. Угол  , т. е.
, т. е. 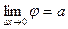 .
.
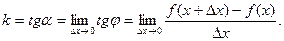
 определена на некотором интервале
определена на некотором интервале  . Проделаем следующие операции:
. Проделаем следующие операции: дадим приращение
дадим приращение  ;
; ;
;
 :
: и обозначают одним из символов
и обозначают одним из символов 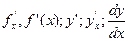 .
.
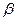 точке
точке  называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
 обозначается одним из символов:
обозначается одним из символов:  или
или  .
.
 , т. е. скорость прямолинейного движения материальной точки в момент времени
, т. е. скорость прямолинейного движения материальной точки в момент времени  описывает какой-либо физический процесс, то производная у' есть скорость протекания этого процесса. В этом состоит физический смысл производной.
описывает какой-либо физический процесс, то производная у' есть скорость протекания этого процесса. В этом состоит физический смысл производной.
 т. е. производная
т. е. производная 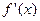 в точке
в точке  равна угловому коэффициенту касательной к графику функции
равна угловому коэффициенту касательной к графику функции  . Пользуясь уравнением прямой, проходящей через заданную точку в заданном направлении
. Пользуясь уравнением прямой, проходящей через заданную точку в заданном направлении  , можно записать уравнение касательной:
, можно записать уравнение касательной:  .
.

 будем рассматривать как функцию количества выпускаемой продукции
будем рассматривать как функцию количества выпускаемой продукции  . Пусть
. Пусть  – прирост продукции, тогда
– прирост продукции, тогда  – приращение издержек производства и
– приращение издержек производства и  – среднее приращение издержек производства на единицу продукции. Производная
– среднее приращение издержек производства на единицу продукции. Производная  выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции.
выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции. и
и  – две дифференцируемые в некотором интервале
– две дифференцируемые в некотором интервале  функции.
функции.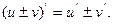 Обозначим
Обозначим  . По определению производной и основным теоремам о пределах получаем:
. По определению производной и основным теоремам о пределах получаем: т.е.
т.е. 
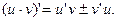
 где
где 

 , если
, если  равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя:
равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя: 
 , тогда
, тогда  сложная функция с промежуточным аргументом
сложная функция с промежуточным аргументом  и независимым аргументом х.
и независимым аргументом х. в точке
в точке  имеет производную
имеет производную  в соответствующей точке
в соответствующей точке 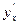 в точке
в точке 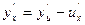 .
. .
. ,
, при
при  .
. .
.
 , в частности,
, в частности, 
 , в частности
, в частности 

 , если
, если  .
. ; 2.
; 2.  ;
; ; 4.
; 4.  ;
; ; 6.
; 6.  ;
;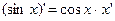 ; 8.
; 8.  ;
; ; 10.
; 10.  ;
; ; 12.
; 12.  ;
; ; 14.
; 14.  ;
; , если для любых
, если для любых  имеет место:
имеет место:  .
. .
.
 .
. такая, что
такая, что 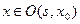
 .
. не определена в этой точке или
не определена в этой точке или  .
. , а для
, а для 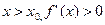 в некоторой окрестности
в некоторой окрестности  , а для
, а для 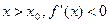 в некоторой окрестности
в некоторой окрестности  в точке
в точке  для любого
для любого  для любого
для любого  .
.



