
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства пределов функции в точке.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Предел функции в точке. Пусть дана функция f(х) с областью определения Х. Определение 1. (по Коши). Число А называется пределом функции f(x) при х→х0, если для любого сколь угодно малого числа e>0 можно указать такое число δ>0 (зависящее от e, δ=δ(e)), что для всех хÎХ таких, что 0<|x-x0|<δ выполняется неравенство |f(х)-A|<e. Т.е.
Замечание. 1) Неравенство (1) не поверяется при х=х0. 2) Принципиальны лишь малые e и d. Пример. 1) f(x)=
|
Геометрический смысл. Неравенство |x-x0|<δ равносильно неравенству х0-δ<x<x0+δ Неравенство |f(х)-A|<E равносильно неравенству A-E<f(x)<A+E Т.е. для всех значений х, попадающих в дельта-окрестность точки х0, соответствующие значения функции попадают в Е-окрестность величины А. Получаем топологическое определение 2. Число А называется пределом функции f(x) при х→х0, если для любого сколь угодно малого числа Е>0 найдется такое число δ>0 (зависящее от Е, δ=δ(Е)), что для всех х, попадающих в дельта-окрестность точки х0, соответствующие значения функции попадают в Е-окрестность величины А.
Принципиальное значение имеют малые окрестности. Определение 3. (по Гейне). Число А называется пределом функции f(x) при х→х0 (в точке х0), если для любой последовательности {xn}, сходящейся к х0 (xn≠x0 Теорема (определение по Гейне, в терминах последовательности). Определения 1 и 3 равносильны, т.е. Для того, чтобы число А было пределом функции f при х→х0 необходимо и достаточно, чтобы для любой последовательности {xn}, сходящейся к х0 (xn≠x0 Доказательство. Необходимость. Пусть Показать, что Т.к. хn→x0, то для d
Достаточность. Дано Допустим противное, что число А не является пределом функции f(x) при х→х0. Т.е. Возьмем dn= Получим, Свойства пределов функции в точке. Теорема 1. Если функция f(x) имеет предел при х→х0 , то этот предел определяется единственным образом. Доказательство. Допустим противное, f(x) имеет 2 предела А≠В при х→х0. Выберем последовательность {xn}→х0 (xn≠x0 Теорема 2. Если функция f(x) имеет предел при х→х0, то на некоторой окрестности V(x0) точки х0 функция f(x) ограничена, т.е. существует число С>0: Доказательство. Пусть Возьмем С=1+çАç. ч.т.д. Предел функции и арифметические операции. Теорема. Пусть 1) 2) 3) 4) Доказательство. Докажем равенство 2. Пусть xn→x0, n→¥, тогда f(xn)→n, n→¥, φ(xn)→n, n→¥. По свойствам предела последовательностей Это равенство доказано для любой переменной xn→x0, n→¥,(xn≠x0), поэтому
Остальные равенства доказываются аналогично. Предел функции и неравенства. Теорема 1. (б.д.) Пусть Теорема 2. Пусть (Т.е. в функциональном неравенстве можно переходить к пределу). Доказательство 1. Допустим, А>B, тогда в некоторой окрестности V(x0) точки х0 Доказательство 2. Через последовательности (сам-но). (Возьмем последовательность xn→x0, n→¥, тогда f(xn)®A, φ(xn)®B и для достаточно больших n f(xn)<φ(xn) (или f(xn)£φ(xn)). По свойствам пределов последовательностей A£B) Следствие. Пусть
Односторонние пределы. Определение. Число А называется правым пределом функции f(x) при х→х0, если для любого сколь угодно малого числа e>0 можно указать такое число δ>0 (зависящее от e, δ=δ(e)), что для всех хÎХ таких, что х0<х<х0+δ выполняется неравенство |f(х)-A|<e. (при попадании точки х в правую полуокрестность точки х0).
f(х0+0)= Определение. Число А называется левым пределом функции f(x) при х→х0, если для любого сколь угодно малого числа e>0 можно указать такое число δ=δ(e), что для всех хÎХ таких, что х0-d<х<х0 выполняется неравенство |f(х)-A|<e. (при попадании точки х в левую полуокрестность точки х0).
f(a-0)= Утверждения. 1) Если у функции f(x) при при х→х0 существует предел А в обычном смысле (т.е. двусторонний), то существуют оба односторонних предела f(х0+0) и f(х0+0) и они оба равны А. 2) Если у функции f(x) при при х→х0 существуют оба односторонних предела f(х0+0) и f(х0+0) и они оба равны А, то у f(x) при при х→х0 существует двусторонний предел, равный числу А. Пример. Расширение понятия предела функции (Понятие предела функции на бесконечности. Бесконечные пределы.) (пример на каждый случай) Определение 1. Число А называется пределом функции f(x) при х→+∞, если для любого сколь угодно малого числа e>0 найдется такое число Т (зависящее от e, Т=Т(e)), что для всех х таких, что x>Т выполняется неравенство |f(х)-A|<e. Т.е.
Определение 2. Число А называется пределом функции f(x) при х→-∞, если для любого сколь угодно малого числа e>0 найдется такое число Т (зависящее от e, Т=Т(e)), что для всех х таких, что x<Т выполняется неравенство |f(х)-A|<e. Т.е. Определение 3. Пределом функции f(x) при х→х0 является +¥, если для любого сколь угодно большого числа С>0 найдется такое число d=d(С), что для всех х таких, что 0<|x-x0|<δ выполняется неравенство f(х)>C. Т.е. Определение 4. Пределом функции f(x) при х→х0 является -¥, если для любого числа С<0 найдется такое число d=d(С), что для всех х таких, что 0<|x-x0|<δ выполняется неравенство f(х)<C. Т.е. Пример. f(x)= Определение 5. Пределом функции f(x) при х→+¥ является +¥, если для любого сколь угодно большого числа С>0 найдется такое число T=T(С), что для всех х таких, что x>T выполняется неравенство f(х)>C. Т.е. Определение 6. Пределом функции f(x) при х→+¥ является -¥, если для любого числа С<0 найдется такое число T=T(С), что для всех х таких, что x>T выполняется неравенство f(х)<C. Т.е. Определение 7. Пределом функции f(x) при х→-¥ является +¥, если для любого сколь угодно большого числа С>0 найдется такое число T=T(С), что для всех х таких, что x<T выполняется неравенство f(х)>C. Т.е. Определение 8. Пределом функции f(x) при х→-¥ является -¥, если для любого числа С<0 найдется такое число T=T(С), что для всех х таких, что x<T выполняется неравенство f(х)<C. Т.е. Свойства пределов. 1. +¥+(+¥)=+¥ -¥+(-¥)=-¥ 2. +¥×+¥=+¥ -¥×(-¥)=+¥ ±¥×А=
±¥×0=0 3. [ Предел композиции функции. Теорема. Пусть даны функции f и φ: 1) 2) То Доказательство. Возьмем произвольную последовательность {xn}, xnÎX, xn≠x0. xn→x0,n→¥. Покажем, что f(φ(xn))→A, n→¥. Т.к. xn→x0,n→¥, φ(х)→ u0, х→х0, то φ(хn)→u0, n→¥. Т.к. f(u)→A, u→u0, то возьмем последовательность un=φ(хn)→u0, n→¥, т.е. f(un)=f(φ(xn))→A, n→¥. А это и означает, что Свойства б/б величин. 1. Если одна из трех функций f(x), -f(x), çf(x)ç является б.б. при х→х0, то и две другие функции также являются б.б. при х→х0. 2. Произведение б/б функции на функцию, предел которой отличен от нуля, есть б/б величина. 3. Сумма б/б величины и ограниченной функции есть б/б величина. 4. Частное от деления б/б функции на функцию, имеющую предел, есть б/б функция. Например, функция f(x)= Доказательство св-ва 2. (остальные – аналогично). Пусть f(x) – б.б. функция при х→х0, т.е. Докажем, что f(x)×j(х) - б.б. функция при х→х0. Рассмотрим последовательность хn→x0, n→¥ (предполагается, что xn берутся из окрестности x0 и xn≠x0) По условию По условию f(x) – б.б. функция при х→х0, но тогда и f(xn) – б.б. функция при n→¥. Следовательно, f(xn)×j(хn) - б.б. последовательность, как произведение б.б. последовательности и последовательности, имеющей конечный, отличный от 0 предел. Т.к. последовательность хn – любая сходящаяся к х0, то заключаем, что
Это означает, что функция f(x)×j(х) - б.б. функция при х→х0. ч.т.д. Алгебраические методы. а) Разложение на множители. б) Устранение иррациональности. в) Выделение главного члена. Пределы монотонных функций. Теорема 1. (б.д.?)Пусть функция f(x) монотонно возрастает (строго возрастает) на множестве Х. Пусть в любой левой полуокрестности точки х0 (х0-d;х0) существуют точки множества Х, отличные от х0. (Число х0 может быть как конечным, так и равным +¥, в этом случае левая полуокрестность это 1) Если при этом функция f(x) ограничена сверху, т.е. существует число С такое, что f(x)£С 2) Если f(x) сверху не ограничена, то Доказательство. 1) Т.к. функция f(x) ограничена сверху, тогда существует точная верхняя граница множества {f(x)}, xÎX. Пусть m=
Возьмем сколь угодно малое e>0 и рассмотрим число m-e. Т.к. m-e<m, то по свойству супремума на множестве {f(x)}, xÎX, обязательно найдется элемент Т.к. функция f(x) монотонно возрастает на множестве Х, то Т.о. m-e<f(x)£m, значит, m-e<f(x)£m+e Ûçf(x)-mç<e. а) Положим d=а- б) Положим D= 2) (б.д.?) Допустим, что функция f(x) не ограничена сверху, т.е. не ограничено сверху множество {f(x)}, xÎX. Это значит, что какое бы большое число М>0 ни взять на множестве {f(x)}, xÎX, обязательно найдется хотя бы один элемент Т.к. функция f(x) монотонно возрастает на множестве Х, то а) Положим d=а- б) Положим D= Теорема 2. Пусть функция f(x) монотонно убывает (строго убывает) на множестве Х. Пусть в любой левой полуокрестности точки х0 (х0-d;х0) существуют точки множества Х, отличные от х0. (Число х0 может быть как конечным, так и равным +¥, в этом случае левая полуокрестность это 1) Если при этом функция f(x) ограничена снизу, т.е. существует число М, такое, что f(x)³М 2) Если f(x) снизу не ограничена, то Предел функции в точке. Пусть дана функция f(х) с областью определения Х. Определение 1. (по Коши). Число А называется пределом функции f(x) при х→х0, если для любого сколь угодно малого числа e>0 можно указать такое число δ>0 (зависящее от e, δ=δ(e)), что для всех хÎХ таких, что 0<|x-x0|<δ выполняется неравенство |f(х)-A|<e. Т.е.
Замечание. 1) Неравенство (1) не поверяется при х=х0. 2) Принципиальны лишь малые e и d. Пример. 1) f(x)=
|
Геометрический смысл. Неравенство |x-x0|<δ равносильно неравенству х0-δ<x<x0+δ Неравенство |f(х)-A|<E равносильно неравенству A-E<f(x)<A+E Т.е. для всех значений х, попадающих в дельта-окрестность точки х0, соответствующие значения функции попадают в Е-окрестность величины А. Получаем топологическое определение 2. Число А называется пределом функции f(x) при х→х0, если для любого сколь угодно малого числа Е>0 найдется такое число δ>0 (зависящее от Е, δ=δ(Е)), что для всех х, попадающих в дельта-окрестность точки х0, соответствующие значения функции попадают в Е-окрестность величины А.
Принципиальное значение имеют малые окрестности. Определение 3. (по Гейне). Число А называется пределом функции f(x) при х→х0 (в точке х0), если для любой последовательности {xn}, сходящейся к х0 (xn≠x0 Теорема (определение по Гейне, в терминах последовательности). Определения 1 и 3 равносильны, т.е. Для того, чтобы число А было пределом функции f при х→х0 необходимо и достаточно, чтобы для любой последовательности {xn}, сходящейся к х0 (xn≠x0 Доказательство. Необходимость. Пусть Показать, что Т.к. хn→x0, то для d Достаточность. Дано Допустим противное, что число А не является пределом функции f(x) при х→х0. Т.е. Возьмем dn= Получим, Свойства пределов функции в точке. Теорема 1. Если функция f(x) имеет предел при х→х0 , то этот предел определяется единственным образом. Доказательство. Допустим противное, f(x) имеет 2 предела А≠В при х→х0. Выберем последовательность {xn}→х0 (xn≠x0 Теорема 2. Если функция f(x) имеет предел при х→х0, то на некоторой окрестности V(x0) точки х0 функция f(x) ограничена, т.е. существует число С>0: Доказательство. Пусть Возьмем С=1+çАç. ч.т.д.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 2777; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.185.6 (0.011 с.) |

 e>0
e>0 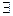 δ=δ(E)
δ=δ(E)  |f(х)-A|<e (1)
|f(х)-A|<e (1) , f(x)→A, x→x0
, f(x)→A, x→x0 . Покажем, что
. Покажем, что 
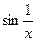 ½£|2х|=2½х½<e Þd=
½£|2х|=2½х½<e Þd=  , тогда
, тогда V(x0)\{x0}
V(x0)\{x0} 



 , тогда
, тогда 
 , то
, то  не стремиться к А при n→¥. Получили противоречие. Следовательно,
не стремиться к А при n→¥. Получили противоречие. Следовательно, 
 , тогда
, тогда =А±В
=А±В

 (если φ(x)≠0, B≠0)
(если φ(x)≠0, B≠0)
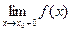 =
=  = А+ или f(x0+0)=A
= А+ или f(x0+0)=A
 =А-. или f(x0-0)=A
=А-. или f(x0-0)=A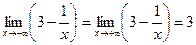 (График).
(График). =А
=А

 =А
=А =+¥
=+¥ - график.
- график.
 =0
=0  =0 (А≠0)
=0 (А≠0) ], [
], [ 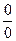 ], [∞-∞], [1∞] - неопределенности
], [∞-∞], [1∞] - неопределенности , х0 – предельная точка множества Х, u0– предельная точка множества U. Если выполнено условие:
, х0 – предельная точка множества Х, u0– предельная точка множества U. Если выполнено условие: =u0 (φ(х)≠х0)
=u0 (φ(х)≠х0) =А,
=А, =А (х0 и u0 могут совпадать с ±¥)
=А (х0 и u0 могут совпадать с ±¥) - является частным от деления б/б функции tg x при х→П/2 на функцию 2х+5 имеющую предел П+5 при х→П/2.
- является частным от деления б/б функции tg x при х→П/2 на функцию 2х+5 имеющую предел П+5 при х→П/2. =∞ и
=∞ и  =с (с≠0).
=с (с≠0). =с (с≠0).
=с (с≠0).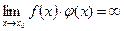
 =
=  = 10. ([
= 10. ([  ( [
( [  ( [
( [  .
. . Тогда
. Тогда  >m-e.
>m-e. будет f(x)³
будет f(x)³ 
 =+¥.
=+¥. .
.


