Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бесконечно малые функции (величины) и их свойства.Содержание книги
Поиск на нашем сайте
Определение. Функция α (х) называется бесконечно малой (б/м) функцией при х → х0, или при х → ∞, если: Т.е. Аналогично можно сформулировать определение бесконечно малой при х → ∞
Например, y=cos x - б/м при х→П/2, у= Связь бесконечно малых величин с пределами функций. Теорема. Функция f(x) имеет при х→х0 (х → ∞) предел, равный А, тогда и только тогда, когда ее можно представить как сумму числа A и бесконечно малой функции α(х) при х → х0 (х → ∞).
Доказательство.Необходимость. Докажем теорему для любого случая х→х0. По условию Достаточность. □ По условию α(х)=f(x)–A есть бесконечно малая при х→х0, то для любого числа ε>0 существует такое число δ>0, что при всех х≠х0 и удовлетворяющих условию |х–х0|<δ верно неравенство |α(х)|=|f(x)–A|<ε. Это и означает, что Доказательство через последовательности. Необходимость. Возьмем последовательность х1,x2,…,xn,… значений х любую, но такую, что xnÎ По условию Т.к. последовательность х1,x2,…,xn,…-любая, сходящаяся к х0, то Û Достаточность. Возьмем последовательность х1,x2,…,xn,… значений х любую, но такую, что xnÎ По условию a(х)=f(x)–A – б.м. при х®х0, т.е. α(хn)®0 при n®¥Û(f(xn)-A)®0 при n®¥. Т.к. последовательность х1,x2,…,xn,…-любая, сходящаяся к х0, то Свойства бесконечно малых величин: 1. Если одна из трех функций f(x), -f(x), çf(x)ç является б.м. при х→х0, то и две другие функции также являются б.м. при х→х0. 2. Алгебраическая сумма конечного числа б/м величин есть величина б/м. 3. Произведение б/м величины на ограниченную функцию (в том числе на постоянную, на другую б/м) есть величина б/м.
4. Частное от деления б/м величины на функцию, предел которой отличен от нуля, есть величина б/м. Доказательство через последовательности или через определение предела функции при А=0. Пример. Доказать, что функция f(x)=(х-1)sin Т.к. Бесконечно большие функции (величины). Определение. Функция β(х) называется бесконечно большой величиной (б/б) при х→х0, если либо При этом в случае, когда Например, функция у=tg x при х→П/2 – б/б; Функция у=х2+5 при х→∞ - б/б; у= Замечание. х0 может означать и конечное число, и один из символов ¥, +¥, -¥. Любая б/б функция является неограниченной. Обратное неверно. Так, например, функция у=хcos х – неограниченная функция, но б/б не является, т.к. при х→∞ функция колеблется, переходя от отрицательных значений к положительным и наоборот, принимая значения 0. Свойства б/б величин. 1. Если одна из трех функций f(x), -f(x), çf(x)ç является б.б. при х→х0, то и две другие функции также являются б.б. при х→х0. 2. Произведение б/б функции на функцию, предел которой отличен от нуля, есть б/б величина. 3. Сумма б/б величины и ограниченной функции есть б/б величина. 4. Частное от деления б/б функции на функцию, имеющую предел, есть б/б функция. Например, функция f(x)= Доказательство св-ва 2. (остальные – аналогично). Пусть f(x) – б.б. функция при х→х0, т.е. Докажем, что f(x)×j(х) - б.б. функция при х→х0. Рассмотрим последовательность хn→x0, n→¥ (предполагается, что xn берутся из окрестности x0 и xn≠x0) По условию По условию f(x) – б.б. функция при х→х0, но тогда и f(xn) – б.б. функция при n→¥. Следовательно, f(xn)×j(хn) - б.б. последовательность, как произведение б.б. последовательности и последовательности, имеющей конечный, отличный от 0 предел.
Т.к. последовательность хn – любая сходящаяся к х0, то заключаем, что
Это означает, что функция f(x)×j(х) - б.б. функция при х→х0. ч.т.д.
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.230.170 (0.008 с.) |

 α (х)=0. х0 может быть как число, так и -¥,+¥,¥.
α (х)=0. х0 может быть как число, так и -¥,+¥,¥. ε > 0
ε > 0 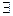 δ=δ(ε)> 0
δ=δ(ε)> 0  |α(х)|<ε
|α(х)|<ε б/м при х→∞.
б/м при х→∞.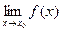 =А
=А 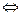 f(x)-A=α(x)
f(x)-A=α(x) f(x) = A. Это означает, что для любого ε > 0 существует такое число δ>0, что для всех х≠х0 и удовлетворяющих условию |х–х0|<δ будет верно неравенство |f(x)–A|<ε, или, обозначив α(х)=f(x)–A, справедливо неравенство |α(х)|<ε. Это и означает, что α(х) есть бесконечно малая при х→ х0. ■
f(x) = A. Это означает, что для любого ε > 0 существует такое число δ>0, что для всех х≠х0 и удовлетворяющих условию |х–х0|<δ будет верно неравенство |f(x)–A|<ε, или, обозначив α(х)=f(x)–A, справедливо неравенство |α(х)|<ε. Это и означает, что α(х) есть бесконечно малая при х→ х0. ■ и xn®x0 при n®¥.
и xn®x0 при n®¥.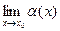 = 0Û
= 0Û = 0. А последнее и означает, что разность f(x)–A – б.м. при х®х0.
= 0. А последнее и означает, что разность f(x)–A – б.м. при х®х0.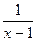 является бесконечно малой при х→1.
является бесконечно малой при х→1. =0, т.е. (х-1) – б.м. при х→1, а функция sin
=0, т.е. (х-1) – б.м. при х→1, а функция sin 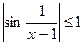 ), то функция f(x) является произведением б.м. функции на ограниченную. Следовательно, функция f(x)=(х-1)sin
), то функция f(x) является произведением б.м. функции на ограниченную. Следовательно, функция f(x)=(х-1)sin 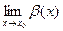 =∞, либо
=∞, либо  - является частным от деления б/б функции tg x при х→П/2 на функцию 2х+5 имеющую предел П+5 при х→П/2.
- является частным от деления б/б функции tg x при х→П/2 на функцию 2х+5 имеющую предел П+5 при х→П/2. =∞ и
=∞ и  =с (с≠0).
=с (с≠0). =с (с≠0).
=с (с≠0).