
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь между б/б и б/м функциями.Содержание книги Поиск на нашем сайте
Теорема. Если функция α(х) – б/м величина при х→х0 (х→∞), то функция β(х)= Доказательство. Пусть α(х) – б/м величина при х→х0 (х→∞), тогда
Последнее неравенство равносильно неравенству Сравнение бесконечно малых величин. Пусть при х→х0 функции α(х) и β(х) являются б.м., и пусть β(х)≠0 1. если Пишут a(х)=о(b(х)) при х→х0 (о малое) Пример. Покажем, что при х→0 функция хk (k>1) – б.м. более высокого порядка, чем х. Действительно, 2. если Пример. Покажем, что при х→0 функции sin kx и mx (k≠0,m≠0)- б.м. одного порядка. Действительно, 3. если Пример. Покажем, что при х→0 функции sin x и tg x (k≠0,m≠0)- б.м. одного порядка. Действительно, 4. если 5. если отношение Пример. Функции a(х)= 6. если Из предыдущих пунктов следует, что 1) Если n=1, то функция α(х) б.м. одного порядка с β(х) при х→х0. 2) Если n>1, то функция α(х) б.м. более высокого порядка по сравнению с β(х) при х→х0. 3) Если n<1, то функция α(х) б.м. более низкого порядка по сравнению с β(х) при х→х0. Теорема 1. Произведение двух б.м. величин является б.м. величиной более высокого порядка по сравнению с каждым из сомножителей. Доказательство. Пусть при х→х0 функции α(х) и β(х) являются б.м., γ(х)=α(х)×β(х). Докажем, что γ(х)=о(α(х)) и γ(х)=о(β(х)) при х→х0. Имеем
Аналогично, Теорема 2. Разность двух эквивалентных бесконечно малых функций является бесконечно малой функцией по сравнению с каждой из них. Доказательство. Пусть при х→х0 функции α(х) и β(х) являются б.м., и α(х)~β(х). Положим γ(х)=α(х)-×β(х). Докажем, что γ(х)=о(α(х)) и γ(х)=о(β(х)) при х→х0. Имеем
Аналогично, Теорема 3 (о замене бесконечно малых при отыскании предела отношения). Пусть функции α(х) и β(х) являются б.м. при х→х0, и α(х)~
То к этому же пределу стремится при х→х0 и отношение Доказательство. 1) Пусть По условию, каждый из сомножителей в правой части имеет конечный предел при х→х0. Тогда 2) Пусть По доказанному в пункте 1), Значит, и в этом случае Замечание 1. Применение теоремы 3 требует знания б.м. функций 1) sin x~x при х→0 (т.к. 2) tg x~x, при х→0 3) 1-cos x~ 4) ln(1+x) ~x, при х→0 5) ex-1~x, при х→0 6)ax-1~xlna, при х→0 (a>0, a≠0) 7) (1+x)a-1~ax, при х→0 8) arcsin x~x, при х→0 9) arctg x~x, при х→0 Покажем, что ln(1+x) ~x, т.е.
Замечание 2. Теорему 3 можно также применять в следующих случаях: Если выражение под знаком предела содержит б/м величину в виде множителя, в виде отношения или в виде показателя степени, то ее можно заменить на эквивалентную ей б/м.
α(х)~β(х) Раскрытие неопределенностей. Если при подстановке предельного значения х в выражение под знаком предела получается величина вида [ Способы устранения неопределенностей.
Алгебраические методы. а) Разложение на множители. б) Устранение иррациональности. в) Выделение главного члена. Применение замечательных пределов. а) при тригонометрических выражениях б) при неопределенности [1∞]. Метод эквивалентных б/м функций. Примеры. С помощью замены эквивалентных найти пределы: 1) 2) 3) =
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.126.111 (0.009 с.) |

 является б/б при х→х0 (х→∞). И наоборот, если функция β(х) – б/б величина при х→х0 (х→∞), то функция α(х)=
является б/б при х→х0 (х→∞). И наоборот, если функция β(х) – б/б величина при х→х0 (х→∞), то функция α(х)=  является б/м при х→х0 (х→∞).
является б/м при х→х0 (х→∞). ε > 0
ε > 0 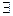 δ=δ(ε)> 0
δ=δ(ε)> 0  |α(х)|<ε
|α(х)|<ε >
> 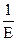 или |β(х)|>M, где М=
или |β(х)|>M, где М=  тогда
тогда , то α(х) называется б.м. более высокого порядка, чем β(х) (α(х) имеет более высокий порядок малости, чем β(х) при х→х0)
, то α(х) называется б.м. более высокого порядка, чем β(х) (α(х) имеет более высокий порядок малости, чем β(х) при х→х0)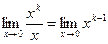 =0, т.к. по условию k>1.
=0, т.к. по условию k>1. =А≠0, то α(х) и β(х) называются б.м. одного порядка (имеют одинаковую «скорость» стремления к 0).
=А≠0, то α(х) и β(х) называются б.м. одного порядка (имеют одинаковую «скорость» стремления к 0).
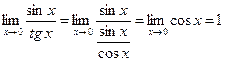
 и b(х)=х – б.м. при х→0. Имеем
и b(х)=х – б.м. при х→0. Имеем  , но
, но 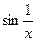 не имеет предела при х→0. Значит, α(х) и β(х) не сравнимы при х→0.
не имеет предела при х→0. Значит, α(х) и β(х) не сравнимы при х→0. =А≠0, то α(х) называется б.м. n –го порядка относительно β(х) при х→х0. (n>0, не обязательно целое).
=А≠0, то α(х) называется б.м. n –го порядка относительно β(х) при х→х0. (n>0, не обязательно целое). , а это означает, что γ(х)=о(α(х)) при х→х0.
, а это означает, что γ(х)=о(α(х)) при х→х0. , а это означает, что γ(х)=о(β(х)) при х→х0. ч.т.д.
, а это означает, что γ(х)=о(β(х)) при х→х0. ч.т.д. , По условию, т.к. α(х)~β(х), то
, По условию, т.к. α(х)~β(х), то  =1. Следовательно,
=1. Следовательно,  =1-1=0. Значит, γ(х)=о(α(х)) при х→х0.
=1-1=0. Значит, γ(х)=о(α(х)) при х→х0. , По условию, т.к. α(х)~β(х), то
, По условию, т.к. α(х)~β(х), то  =1-1=0. Значит, γ(х)=о(β(х)) при х→х0. ч.т.д.
=1-1=0. Значит, γ(х)=о(β(х)) при х→х0. ч.т.д. (х), β(х) ~
(х), β(х) ~  (х) при х→х0. Тогда если существует конечный или бесконечный предел
(х) при х→х0. Тогда если существует конечный или бесконечный предел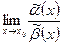 ,
, .
.
 =
= 

 =1×с×1=с. Т.е.
=1×с×1=с. Т.е.  =0 (считаем, что
=0 (считаем, что 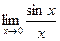 =0),
=0), , при х→0
, при х→0 =1
=1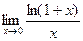 =
= 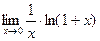 =
=  =ln
=ln  (т.к. функция ln x непрерывна)=ln e=1. Ч.т.д.
(т.к. функция ln x непрерывна)=ln e=1. Ч.т.д.
 ], [
], [ 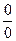 ], [∞-∞], [1∞], то говорят, что имеет место соответствующая неопределенность.
], [∞-∞], [1∞], то говорят, что имеет место соответствующая неопределенность. =
=  = 10. ([
= 10. ([  ( [
( [  ( [
( [ 
 . Имеем ln(1+3x) ~3x, sin 5x~5x. Поэтому
. Имеем ln(1+3x) ~3x, sin 5x~5x. Поэтому 
 . Имеем
. Имеем 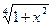 ~
~  x2, ln(cosx)=ln(1+(cosx-1))~cosx-1. Поэтому
x2, ln(cosx)=ln(1+(cosx-1))~cosx-1. Поэтому  =-2
=-2 =
=  =
=  =
= 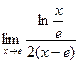 =
=  =
= =
= 



