
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комплексные числа. Свойства. Формы записи.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
БИЛЕТ1 Комплексные числа. Свойства. Формы записи. Комплексным числом называется выражение вида Свойства комплексных чисел: 1) комплексные числа коммутативны по сложению и по умножению.
3) комплексные числа дистрибутивны.
Для комплексных чисел операция деления определена как операция обратная операции умножения. Если
Формы записи: Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи. Алгебраическая форма - это такая форма записи комплексных чисел, при которой комплексное число z, заданное парой вещественных чисел (x, y), записывается в виде
где использован символ i, называемый мнимой единицей. Тригонометрическая форма записи комплексного числа Из формулы
где r и φ - модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству Формула Эйлера. Экспоненциальная форма записи комплексного числа Формула Эйлера: cos φ + i sin φ = e i φ. Из формулы Эйлера и тригонометрической формы записи комплексного числа вытекает, что любое отличное от нуля комплексное число
где r и φ - модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству БИЛЕТ 2. Интегрирование простейших рациональных функций Для интегрирования рациональной функции
1)Если дробь неправильная (т.е. степень P (x) больше степени Q (x)), преобразовать ее в правильную, выделив целое выражение;
4)Вычислить интегралы от простейших дробей. Рассмотрим указанные шаги более подробно.
Шаг 1. Преобразование неправильной рациональной дроби Если дробь неправильная (т.е. степень числителя P (x) больше степени знаменателя Q (x)), разделим многочлен P (x) на Q (x). Получим следующее выражение:
Шаг 2. Разложение знаменателя на простейшие дроби Запишем многочлен знаменателя Q (x) в виде
Шаг 3. Разложение рациональной дроби на сумму простейших дробей. Запишем рациональную функцию в следующем виде:
Затем умножим обе части полученного уравнения на знаменатель Q (x) и приравняем коэффициенты при слагаемых с одинаковыми степенями x. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов Ai, Bi, Ki, Li, Mi, Ni,.... Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов.
Шаг 4. Интегрирование простейших рациональных дробей. Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул: 1) 2)
У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат:
где 3) 4) 5) Интеграл 6.
БИЛЕТ 3 БИЛЕТ4 БИЛЕТ5 5. Интегрирование иррациональных функций Пусть
Если заменить в
Этот интеграл рационализируется с помощью подстановки
В самом деле, так как подкоренное выражение представляет собой дробно-линейную относительно
Тогда
Замечание. Если под знаком интеграла содержатся корни с разными показателями, но с одним и тем же дробно-линейным относительно х подкоренным выражением, то сначала следует привести их к одному показателю, после чего использовать указанный прием.
БИЛЕТ6 6. Интегрирование диф. бинома (теорема Чебышёва) Дифференциальным биномом называют выражение вида
где a и b — любые константы, а показатели степеней m, n и p — рациональные числа. Изучим вопрос об интегрируемости в элементарных функциях дифференциальных биномов.
Подынтегральная функция в правой части является дробно-линейной иррациональностью следующего вида вида
3. Третьему случаю соответствует целому число
БИЛЕТ7 7.Специальные функции- функции которые выражаются через элементарные функции, представляются в виде рядов или интегралов. Интеграл неберущийся –если подынтегральная функция не является элементарной. Эти интегралы не выражают через элементарные функции, поэтому для них вычисляют вероятности для нормальной распределенной случайной величины этой функции. 3 метода вычислений:1приближенный метод Симсона 2.разложение подынтегральной функции в ряд Маклорена 3.с помощью таблицы значений функций Лапласа Примеры: 1.
БИЛЕТ8 8. Пусть функция у=ƒ(х) определена на отрезке [а; b], а < b. Выполним следующие действия. 1. С помощью точек х0=а, x1, х2,..., хn = В (х0 <x1 <...< хn) разобьем отрезок [а, b] на n частичных отрезков [х0;х1], [x1; х2],..., [хn-1,хn] (см. рис. 167).
2. В каждом частичном отрезке [xi-1;xi], i = 1,2,...,n выберем произвольную точку сi є [xi-1; xi] и вычислим значение функции в ней, т. е. величину ƒ(сi). 3. Умножим найденное значение функции ƒ (сi) на длину ∆xi=xi-xi-1 соответствующего частичного отрезка: ƒ (сi) • ∆хi. 4. Составим сумму Sn всех таких произведений:
Сумма вида (35.1) называется интегральной суммой функции у = ƒ(х) на отрезке [а; b]. Обозначим черезλ длину наибольшего частичного отрезка: λ = max ∆xi(i = 1,2,..., n). БИЛЕТ9 9. Физический смысл: 1) если задана скорость как функция от времени, то путь за время Т равен интегралу от скорости по времени;
2) если задано ускорение как функция от времени, то изменение скорости равно интегралу от ускорения по времени; Геометрический смысл: если функция y(x) больше нуля на промежутке [a;b], то площадь криволинейной трапеции, ограниченной графиком функции, осью ОХ и двумя прямыми х=а и х=b, равна интегралу от этой функции по переменной х на данном промежутке. БИЛЕТ10 10. Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x), вычислить ее значения в точках a и b и найти разность F(b) – F(a). БИЛЕТ11
БИЛЕТ12 12. Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий. · Область интегрирования является бесконечной. Например, является бесконечным интервалом · Функция f(x) неограничена в области интегрирования. Если интервал [a,b] конечный, и функция интегрируема по Риману, то значение несобственного интеграла совпадает с значением определённого интеграла. Несобственные интегралы I рода Пусть 1. Если 2. Если не существует конечного Пусть
1. Если 2. Если не существует конечного Если функция
Примеры
БИЛЕТ13 БИЛЕТ15 БИЛЕТ16 БИЛЕТ17 17. Вычисление дуги плоской кривой Пусть известна функция
БИЛЕТ18 18. Вычисление площади поверхности и объёма тела вращения Указанную площадь можно получить вычислением определенного интеграла:
-Тело образованно вращением вокруг оси абсцисс криволинейной трапеции, расположенно в верхней полуплоскости и ограниченной осью абсцисс, прямыми
БИЛЕТ19 Вопрос 19
БИЛЕТ20 Вопрос 20 БИЛЕТ21 Вопрос 21 Формула метода трапеций.
Формула метода Симпсона (парабол) имеет вид Графическая иллюстрация метода парабол (Симпсона). Красной линией изображен график функции y=f(x), синей линией показано приближение графика функции y=f(x) квадратичными параболами на каждом элементарном отрезке разбиения.
БИЛЕТ22 Исследование пределов и непрерывности в многомерных пространствах приводит ко многим нелогичным и патологическим результатам, не свойственным функциям одной переменной. Например, существуют скалярные функции двух переменных, имеющих точки в области определения, которые при приближении вдоль произвольной прямой дают специфический предел, и дают другой предел при приближении вдоль параболы. Функция
стремится к нулю по любой прямой, проходящей через начало координат. Однако, когда к началу координат приближаются вдоль параболы
Функция Функция Функция
БИЛЕТ23 Вопрос 23 Частная производная обобщает понятие производной на случай нескольких измерений. Частная производная функции нескольких переменных — это производная относительно одной переменной, все другие переменные при нахождении считаются константами. Для упрощения ограничимся случаем функций от трех переменных; все дальнейшее, однако, справедливо и для функций любого числа переменных. Пусть в некоторой области Аналогично определяются и частные производные функции Дифференциальные уравнения, содержащие частные производные, называют дифференциальными уравнениями в частных производных или (Д)УЧП. Эти уравнения как правило сложнее для решения чем обычные дифференциальные уравнения, которые содержат производные относительно только одной переменной.
БИЛЕТ24 Вопрос 24 Пусть задана функция f(x, y). Тогда каждая из ее частных производных(если они, конечно, существуют)
и, аналогично,
Производные
БИЛЕТ25 25. Дифференцируемость и полный дифференциал функции двух переменных. Теорема о равенстве смешанных производных высших порядков. Пусть функция Функция
где Главная часть приращения функции
Выражения
Теорема 1 (необходимое условие дифференцируемости функции). Если функция Так как функция дифференцируема в точке М, то имеет место равенство (1). Отсюда вытекает, что Это означает, что функция непрерывна в точке М. Положив
Равенство (1) можно записать в виде
где
Отметим, что обратное утверждение не верно, т. е. из непрерывности функции или существования частных производных не следует дифференцируемость функции. Так, непрерывная функция Как следствие теоремы получаем формулу для вычисления полного дифференциала. Формула (3) принимает вид:
или
где Теорема 2 (достаточное условие дифференцируемости функции).Если функция Отметим, что для функции Чтобы функция Арифметические свойства и правила исчисления дифференциалов функции одной переменной сохраняются и для дифференциала функции двух (и большего числа) переменных. Из определения дифференциала функции
Так как полное приращение
Формулой (7) пользуются в приближенных расчетах. Отметим, что с помощью полного дифференциала можно найти: границы абсолютной и относительной погрешностей в приближенных вычислениях; приближенное значение полного приращения функции и т. д. Теорема: Если в некоторой окрестности точки
БИЛЕТ26 26. Пусть функция
Аналогично определяются дифференциалы более высоких порядков. Определение: Дифференциалом
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1924; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.101.107 (0.015 с.) |

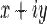 , где
, где  — действительные числа
— действительные числа  ;
; 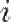 — число, квадрат которого равен минус единице
— число, квадрат которого равен минус единице 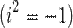 ; число обозначается
; число обозначается 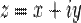 .
.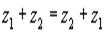
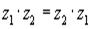
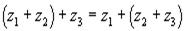
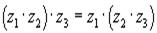
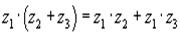
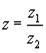 , то z является решением уравнения
, то z является решением уравнения 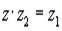 . Решим это уравнение, домножив левую и правую часть на
. Решим это уравнение, домножив левую и правую часть на 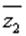 и разделив обе части на квадрат модуля. Получим, что
и разделив обе части на квадрат модуля. Получим, что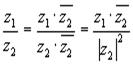
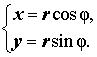 вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде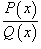 , где P (x) и Q (x) - полиномы, используется следующая последовательность шагов:
, где P (x) и Q (x) - полиномы, используется следующая последовательность шагов: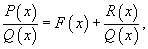
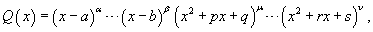
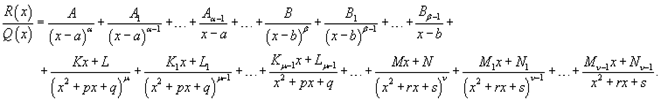
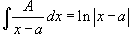
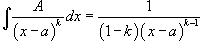

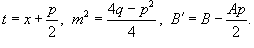 Затем применяются следующие формулы:
Затем применяются следующие формулы: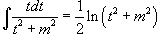
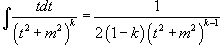
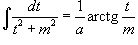
 может быть вычислен за k шагов с помощью формулы редукции
может быть вычислен за k шагов с помощью формулы редукции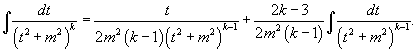
 — рациональная функция от
— рациональная функция от 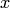 и
и 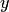 , т. е. функция, получаемая из
, т. е. функция, получаемая из 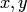 и чисел с помощью конечного числа арифметических операций (сложения, умножения и деления). Примерами таких функций могут служить
и чисел с помощью конечного числа арифметических операций (сложения, умножения и деления). Примерами таких функций могут служить , то получим функцию
, то получим функцию 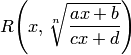 от одной переменной
от одной переменной 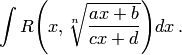
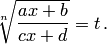
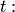
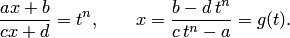
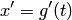 — рациональная функция. Заменяя теперь переменную в данном интеграле, получим интеграл от рациональной функции новой переменной
— рациональная функция. Заменяя теперь переменную в данном интеграле, получим интеграл от рациональной функции новой переменной 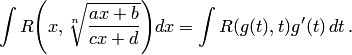
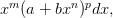
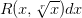 , где r — наименьшее общее кратное знаменателей рациональных чисел m и n. Стало быть, интеграл от дифференциального бинома в этом случае рационализируется подстановкой
, где r — наименьшее общее кратное знаменателей рациональных чисел m и n. Стало быть, интеграл от дифференциального бинома в этом случае рационализируется подстановкой 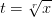 .
.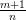 . Сделаем подстановку
. Сделаем подстановку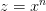 и положим для краткости
и положим для краткости 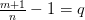 , получим
, получим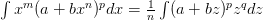
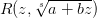 , где s — знаменатель рационального числа p.
, где s — знаменатель рационального числа p.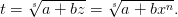
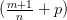 . Подынтегральная функция в правой части является дробно-линиейной иррациональностью вида
. Подынтегральная функция в правой части является дробно-линиейной иррациональностью вида 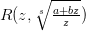 , так что интеграл от дифференциального бинома рационализируется подстановкой вида
, так что интеграл от дифференциального бинома рационализируется подстановкой вида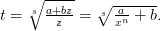
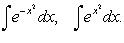 2.
2.  3.
3. 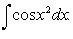 4.
4. 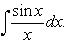
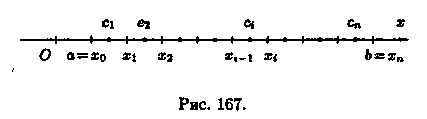
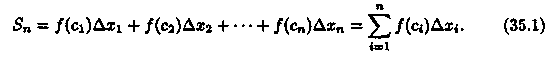
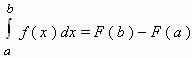
 , где
, где  непрерывна на
непрерывна на 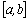 . Введем новую переменную
. Введем новую переменную  , связанную с
, связанную с  равенством
равенством  . Если
1)
. Если
1)  2)
2)  и
и  непрерывны на
непрерывны на  ,
3) при изменении z от α до β значения
,
3) при изменении z от α до β значения  то
то

 –первообразная для функции
–первообразная для функции  . Тогда по формуле Ньютона–Лейбница
. Тогда по формуле Ньютона–Лейбница
 является первообразной для функции
является первообразной для функции  :
:  =[по правилу дифференцирования сложной функции] =
=[по правилу дифференцирования сложной функции] =  Тогда по формуле Ньютона–Лейбница
Тогда по формуле Ньютона–Лейбница

 при x = ln 2
при x = ln 2 
 =
= 
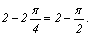

 Пример.
Пример.

 .
. определена и непрерывна на множестве от
определена и непрерывна на множестве от 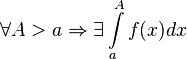 . Тогда:
. Тогда: , то используется обозначение
, то используется обозначение  и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае  (
( или
или  ), то интеграл
), то интеграл  называется расходящимся к
называется расходящимся к  , или просто расходящимся.
, или просто расходящимся. и
и  . Тогда:
. Тогда: , то используется обозначение
, то используется обозначение  и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае  (
( называется расходящимся к
называется расходящимся к  , где с — произвольное число.
, где с — произвольное число.
 и требуется найти длину дуги, заданной функцией
и требуется найти длину дуги, заданной функцией  .
. , где
, где 
 и
и  и графиком непрерывной функции
и графиком непрерывной функции  .
.
 . (1)
. (1)
 . (2)
. (2)
 . (3)
. (3)
 . (4)
. (4)
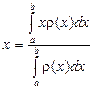 . (5)
. (5)
 . (6)
. (6)
 . (7)
. (7)

 .
.
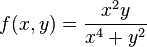
 , предел = 0.5. Так как пределы по разным траекториям не совпадают, предела не существует.
, предел = 0.5. Так как пределы по разным траекториям не совпадают, предела не существует. имеет пределом число A при стремлении переменных
имеет пределом число A при стремлении переменных  , соответственно, к
, соответственно, к  , если для каждого число
, если для каждого число  найдется такое число
найдется такое число  , что
, что  , то есть
, то есть  .
. называется непрерывной в точке
называется непрерывной в точке  , если предельное значение этой функции в точке
, если предельное значение этой функции в точке  .
. , если она непрерывна в каждой точке этого множества.
, если она непрерывна в каждой точке этого множества. имеем функцию
имеем функцию  ; возьмем точку
; возьмем точку  в этой области. Если мы будем считать
в этой области. Если мы будем считать  и
и  за постоянные значения
за постоянные значения  и
и  , и будем менять
, и будем менять  , то
, то 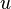 будет функцией от одной переменной
будет функцией от одной переменной  ); можно поставить вопрос о вычислении ее производной в точке
); можно поставить вопрос о вычислении ее производной в точке  . Придадим этому значению
. Придадим этому значению  , тогда функция получит приращение
, тогда функция получит приращение 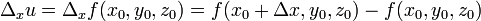 , которое можно было бы назвать ее частным приращением (по
, которое можно было бы назвать ее частным приращением (по  . Эта производная называется частной производной функции
. Эта производная называется частной производной функции  по
по  .
. ) используется для определения понятий градиента, дивергенции, и ротора с точки зрения частных производных. Матрица частных производных — матрица Якоби — может использоваться для представления производной функции (отображения) между двумя пространствами произвольной размерности. Таким образом производная может быть представлена как линейное преобразование, которое изменяется в зависимости от точки из области определения функции.
) используется для определения понятий градиента, дивергенции, и ротора с точки зрения частных производных. Матрица частных производных — матрица Якоби — может использоваться для представления производной функции (отображения) между двумя пространствами произвольной размерности. Таким образом производная может быть представлена как линейное преобразование, которое изменяется в зависимости от точки из области определения функции. и
и  , которые называются также частными производными первого порядка, снова являются функцией независимых переменных x, y и может, следовательно также иметь частные производные. Частная производная
, которые называются также частными производными первого порядка, снова являются функцией независимых переменных x, y и может, следовательно также иметь частные производные. Частная производная 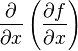 обозначается через
обозначается через  или
или  , а
, а  через
через  или
или  . Таким образом,
. Таким образом,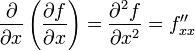 ,
, 
 ,
,  .
. и
и  называются частными производными второго порядка. Определение: Частной производной второго порядка от функции z=f(x;y) дифференцируемой в области D,называется первая производная от соответствующей частной производной. Рассматривая частные производные от них, получим всевозможные частные производные 3 порядка:
называются частными производными второго порядка. Определение: Частной производной второго порядка от функции z=f(x;y) дифференцируемой в области D,называется первая производная от соответствующей частной производной. Рассматривая частные производные от них, получим всевозможные частные производные 3 порядка:  ,
,  ,
,  и т. д.
и т. д. определена в некоторой окрестности точки
определена в некоторой окрестности точки  . Составим полное приращение функции в точке М:
. Составим полное приращение функции в точке М: 
 (1)
(1)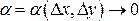 и
и  при
при  . Сумма первых двух слагаемых в равенстве (1) представляет собой главную часть приращения функции..
. Сумма первых двух слагаемых в равенстве (1) представляет собой главную часть приращения функции.. и
и  :
: (2)
(2) и
и  называют частными дифференциалами. Для независимых переменных х и у полагают
называют частными дифференциалами. Для независимых переменных х и у полагают  и
и  . Поэтому равенство (2) можно переписать в виде
. Поэтому равенство (2) можно переписать в виде (3)
(3) и
и  , причем
, причем 


 в равенстве (1), получим:
в равенстве (1), получим:  Отсюда находим
Отсюда находим  Переходя к пределу при
Переходя к пределу при  т. е.
т. е.  Таким образом, в точке М существует частная производная
Таким образом, в точке М существует частная производная  Аналогично показывается, что в точке М существует частная производная
Аналогично показывается, что в точке М существует частная производная 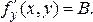
 (4)
(4) при
при  не дифференцируема в точке (0;0).
не дифференцируема в точке (0;0). (5)
(5)

 – частные дифференциалы функции
– частные дифференциалы функции  и
и  в точке М(х, у), то она дифференцируема в этой точке и её полный дифференциал выражается формулой (5).
в точке М(х, у), то она дифференцируема в этой точке и её полный дифференциал выражается формулой (5). одной переменной существование производной
одной переменной существование производной  в точке является необходимым и достаточным условием её дифференцируемости в этой точке.
в точке является необходимым и достаточным условием её дифференцируемости в этой точке. и
и  имеет место приближенное равенство
имеет место приближенное равенство (6)
(6) равенство (6) можно переписать в следующем виде:
равенство (6) можно переписать в следующем виде: (7)
(7) функция
функция  имеет смешанные частные производные
имеет смешанные частные производные  и
и  , причём эти смешанные частные производные непрерывны в точке
, причём эти смешанные частные производные непрерывны в точке  , то они равны в этой точке:
, то они равны в этой точке: 

 зависит от переменной
зависит от переменной  и дифференцируема в точке
и дифференцируема в точке  , рассматриваемый как функция от
, рассматриваемый как функция от  данной функции, который называется дифференциалом второго порядка функции
данной функции, который называется дифференциалом второго порядка функции 
 -го порядка
-го порядка  функции
функции 


