
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комплексное сопротивление и проводимость участков цепиСодержание книги
Поиск на нашем сайте По закону Ома известно что:
Если применить метод комплексных амплитуд при гармоническом воздействии, тогда это отношение можно представить мгновенными комплексными величинами напряжения u(t) и тока i(t):
Физический смысл комплексного сопротивления.
где φu – фаза комплекного напряжения, φi- фаза комплексного тока
-
- алгебраическая форма записи комплексного сопротивления -
- реактивная часть комплексного сопротивления.
- модуль комплексного сопротивления
Векторное представление комплексного сопротивления Для представления комплексного сопротивления на комплексной плоскости можно воспользоваться и алгебраической и показательной формах. Положение точки (сопротивления) зависит от знака действительной и мнимой частей сопротивления, т.е. от аргумента φZ. Угол отсчитывается от действительной оси.
Для третьей четверти
Для четвёртой четверти
Комплексная проводимость участка цепи.
g - резистивная составляющая. b – реактивная составляющая
Схемы замещения комплексного сопротивления и проводимости
Действительную и мнимую части Z и Y можно на схеме изобразить прямоугольником. Сопротивления складываются при последовательном соединении, а проводимости – при параллельном. Следовательно, комплексное сопротивление Z можно представить последовательной схемой, а комплексную проводимость Y – параллельной схемой. Так как между сопротивлением и проводимостью существует однозначная связь, то эти две схемы можно рассматривать как эквивалентные. Можно получить формулы преобразования действительных и мнимых частей Z в Y и наоборот.
Подсчитаем проводимость
Формулы преобразования последовательной схемы в параллельную можно получить на основе принципа дуальности. Дано:
Комплексные сопротивления и проводимости идеализированных элементов (R, L, C) Сопротивление R
Составим цепь из генератора гармонических колебаний (ЭДС) и сопротивления R. Мгновенное комплексное значение тока равно
Таким образом, комплексное сопротивление Z равно самому сопротивлению R, фаза равна нулю.
Вывод: в сопротивлении R ток и напряжение совпадают по фазе. Индуктивность L
Мгновенное комплексное напряжение на индуктивности равно
Вывод: комплексное сопротивление индуктивности является чисто реактивным сопротивлением; сопротивление прямо пропорционально частоте, т.е. зависит от частоты. При ω = 0 => ZL = 0 – индуктивность является короткозамкнутой цепью,
В индуктивности напряжение опережает ток на 900.
Емкость C
Проведем все вычисления, аналогичные индуктивности. К емкости подключен источник гармонического напряжения
При ω = 0 => ZC =¥ т.е ёмкость не пропускает постоянный ток, представляет собой разрыв цепи. При ω = ¥ => ZC =0 т.е ёмкость представляет собой замкнутую цепь т.е. хорошо пропускает высокочастотный ток.
Лекция 7. Резонанс в электрических цепях. Явление резонанса и его значение в радиотехнике и электросвязи. Последовательный колебательный контур. Резонанс напряжений. Частотные характеристики последовательного контура.
Явление резонанса в последовательном колебательном контуре
Рассмотрим цепь, состоящую из генератора гармонического напряжения Ė и последовательного колебательного контура. Цепь линейная, поэтому для определения тока воспользуемся методом комплексных амплитуд.
Решая это уравнение, определим частоту, которую называю резонансной
Она определяется параметрами элементов контура L, C. Ток в контуре на этой частоте достигнет максимальной величины, которая зависит от R.
В радиотехнике такой электрический режим в колебательном контуре называют фазовым резонансом, а частоту ω0 – резонансной частотой. Это название связано с тем, что разность фаз между напряжением и током на этой частоте, т.е. фаза комплексного сопротивления контура равно нулю

Таким образом, условием резонанса в колебательном контуре является x(ω0) = 0. Резонанс возникнет в том случае, если частота сигнала будет равна резонансной частоте контура ω = ω0. Параметры контура. Характеристика резонанса. 1. Резонансное сопротивление контура – сопротивление контура на резонансной частоте. Оно равно сопротивлению потерь и является минимальным
В реальных контурах оно имеет значение от сотен Ом до десятков кОм. 3. Добротность контура
Определяется отношением сопротивления реактивного элемента на резонансной частоте к сопротивлению потерь.
5. Расстройка – это отклонение частоты сигнала от резонансной частоты. Различают три типа расстройки
Обобщенная расстройка
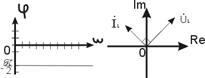
При ω = 0, a( 0) = –¥, ω = ω0, a (ω0) = 0, ω = ¥, a(¥) = ¥. Резонанс в последовательном контуре характеризуется не только разностью фаз между напряжением и током, не только максимальным током, но и величиной напряжения на реактивных элементах.
ÚR = İ·R = E – напряжение на сопротивлении равно ЭДС.
Вывод: амплитуда напряжений на реактивных элементах в Q раз больше ЭДС источника. Поэтому резонанс в последовательном колебательном контуре называют резонансом напряжений. По фазе напряжения ÚC и ÚL противоположны. Основной задачей в радиотехнике является передача информации на расстоянии с помощью радиосигнала. Разделение сигналов т.е каналов связи между собой осуществляется по разным параметрам сигналов. Наиболее часто употребляемым параметром является частота, т.е. по частотному признаку.
S = ω2 - ω1 - ширина канала по частоте. Для разделения каналов между собой в радиотехнике используются устройства “Электрические фильтры ” - цепь, способная пропускать сигналы в заданном диапазоне частот S. (селекция сигналов.) Каждый фильтр должен обладать определённой избирательностью. Избирательность- способность цепи выделить или пропустить сигналы в заданной полосе частот. Полоса частот S, в пределах которой фильтр пропускает сигналы, называется полосой пропускания (ПП).
Электрические фильтры, как правило, выполняются в виде четырёхполюсников. Два полюса 1-1` называются входными, к ним подводится входной сигнал. Клеммы 2-2` называются выходными, к ним подключается нагрузка, на них образуется выходной сигнал после фильтрации.
Он может быть записан в показательной форме, если U 1 и U 2 также записать в показательной форме:
Зависимость модуля от частоты K(ω) называется амплитудно-частотной характеристикой (АЧХ). φk(ω) = φU2 - φU1 - фаза коэффициента передачи или разность фаз напряжений. Зависимость аргумента коэффициента передачи или фазы от частоты называется фазо-частотной характеристикой (ФЧХ).
К частотным характеристикам относится еще одна амплитудно-фазовая характеристика (АФХ) – годограф. Годограф – это геометрическое место точек конца вектора параметра в комплексной плоскости при изменении частоты от 0 до ¥. Годограф можно построить двумя способами, либо в декартовой, либо в полярной системе координат.
На годографе стрелкой показывают изменение частоты. По годографу легко построить АЧХ и ФЧХ. Вывод: АЧХ, ФЧХ, годограф образуют семейство комплексных частотных характеристик.
Принципиальная, упрощённая схемы и схема замещения последовательного колебательного контура
Для изучения свойств контура нужно катушку и конденсатор представить схемами замещения соответственно – (L – RL) и (C – RC). Для упрощения анализа свойств делают преобразования всей схемы в последовательную схему, где R – сопротивление потерь контура, зависящее от сопротивлений RL и RC.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.01 с.) |




 (сократим на
(сократим на  , получим)
, получим) Эту величину называют комплексным сопротивлением.
Эту величину называют комплексным сопротивлением. ,
, - показательная форма комплексного сопротивления.
- показательная форма комплексного сопротивления. - модуль комплексного сопротивления.
- модуль комплексного сопротивления.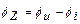 - аргумент комплексного сопротивления.
- аргумент комплексного сопротивления. тригонометрическая форма записи комплексного сопротивления
тригонометрическая форма записи комплексного сопротивления
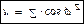 резистивная часть,
резистивная часть,



 Для первой четверти:
Для первой четверти: Для второй четверти
Для второй четверти

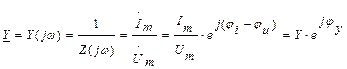 - комплексная проводимость участка цепи.
- комплексная проводимость участка цепи.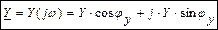 - тригонометрическая форма.
- тригонометрическая форма. -алгебраическая форма
-алгебраическая форма - модуль комплексной проводимости.
- модуль комплексной проводимости.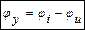 - аргумент комплексной проводимости.
- аргумент комплексной проводимости.
 Необходимо знать связь между комплексным сопротивлением и комплексной проводимостью.
Необходимо знать связь между комплексным сопротивлением и комплексной проводимостью.



 Дано:
Дано:

 Следовательно,
Следовательно,
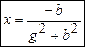
 Получим
Получим


 Комплексное сопротивление Z R равно
Комплексное сопротивление Z R равно


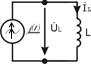
 Пусть индуктивность находится при воздействии гармонического тока (источник тока)
Пусть индуктивность находится при воздействии гармонического тока (источник тока) ,
,  .
. При ω = ¥ => ZL = ¥ - индуктивность является разомкнутой цепью. По формуле Эйлера:
При ω = ¥ => ZL = ¥ - индуктивность является разомкнутой цепью. По формуле Эйлера:  (т.к.
(т.к.  и
и  ).
).

 .
. Подсчитаем комплексное значение тока через емкость
Подсчитаем комплексное значение тока через емкость 

 Вывод: комплексное сопротивление емкости чисто реактивное; оно обратно пропорционально частоте; напряжение на емкости отстает от тока на 900.
Вывод: комплексное сопротивление емкости чисто реактивное; оно обратно пропорционально частоте; напряжение на емкости отстает от тока на 900.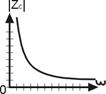
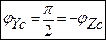


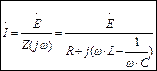

 Мнимая часть сопротивления зависит от частоты и на определенной частоте ω0 она может обратиться в ноль
Мнимая часть сопротивления зависит от частоты и на определенной частоте ω0 она может обратиться в ноль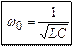
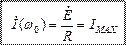


 2. Характеристическое сопротивление - это сопротивление реактивных элементов (индуктивности и емкости) контура на резонансной частоте
2. Характеристическое сопротивление - это сопротивление реактивных элементов (индуктивности и емкости) контура на резонансной частоте
 4. Коэффициент затухания
4. Коэффициент затухания 

 Абсолютная расстройка – Δω = ω – ω0 или Δ f = f – f0.
Абсолютная расстройка – Δω = ω – ω0 или Δ f = f – f0. Относительная расстройка
Относительная расстройка 



 Определим амплитуду напряжения на реактивных элементах на резонансной частоте ω = ω0.
Определим амплитуду напряжения на реактивных элементах на резонансной частоте ω = ω0.
 ω н – несущая частота
ω н – несущая частота
 Основным параметром фильтра является коэффициент передачи по напряжению K u(j ω)
Основным параметром фильтра является коэффициент передачи по напряжению K u(j ω)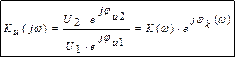
 - модуль коэффициента передачи.
- модуль коэффициента передачи. АЧХ и ФЧХ являются частотными характеристиками параметра, например, коэффициента передачи.
АЧХ и ФЧХ являются частотными характеристиками параметра, например, коэффициента передачи.
 Последовательным колебательным контуром называется цепь, составленная из конденсатора и катушки, соединенные последовательно.
Последовательным колебательным контуром называется цепь, составленная из конденсатора и катушки, соединенные последовательно.


