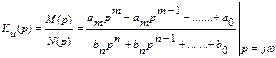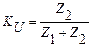Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Избирательность. Полоса пропусканияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
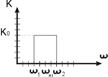
Для чёткого разделения каналов связи между собой, фильтр должен иметь АЧХ прямоугольной формы.Фильтр с такой АЧХ называют идеальным.
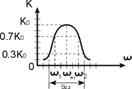
Этот фильтр обладает максимальной избирательностью.Реальный фильтр имеет АЧХ не прямоугольной формы, а колоколообразной. Такой фильтр не обладает максимальной избирательностью. Избирательность количественно можно определить коэффициентом прямоугольности KП, который равен отношению полос пропускания на уровнях 0.3 и 0.7 Коэффициент прямоугольности у идеального фильтра KП.ИД.Ф = 1. Чем больше KП, тем выше избирательность фильтра. В радиотехнике принято полосу пропускания фильтра оценивать на уровне 1/
По полосе пропускания нельзя судить об избирательности фильтра. Классификация фильтров Фильтры можно классифицировать по разным признакам. 1) По положению полосы пропускания фильтра.
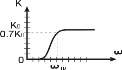
а) Фильтр нижних частот (ФНЧ). Полоса пропускания лежит в пределах 0 ≤ ω ≤ ωгр. ωгр – граничная частота полосы пропускания. б) Фильтр высоких частот (ФВЧ)
Полоса пропускания в пределах ωгр < ω < ¥. в) Полосовой фильтр (ПФ)
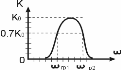
Полоса пропускания лежит между граничными частотами ωгр1 < ω < ωгр2. г) Заградительный (режекторный) фильтр.
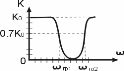
Фильтр не пропускает сигналы с частотами в пределах полосы режекции (не пропускания) ωгр1 < ω < ωгр2. 2) По относительной ширине полосы пропускания. Оценку ведут по сравнению величин полосы пропускания S и средней или заданной частоты ω0. а) Широкополосный фильтр. б) Узкополосный фильтр.
3) По избирательности фильтра. Коэффициент передачи любого фильтра может быть представлен в виде отношения двух полиномов комплексной переменной p = jω.
где m, n – максимальные степени полиномов. Эта форма любого параметра цепи называют операторная форма.
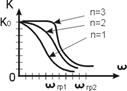
Избирательность зависит от наибольшей степени полинома. Чем выше степень, тем выше избирательность цепи. Чем сложнее цепь, тем выше порядок и выше избирательность. Применение последовательного колебательного контура в качестве режекторного фильтра
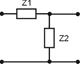
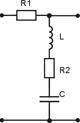
Последовательный контур можно включать в виде двухполюсника в составе Г-образного делителя напряжений.
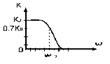
Коэффициент передачи зависит от соотношения величин сопротивлений делителя. Например, если модуль Z2 << Z1, то Ku << 1. Если Z2 >> Z1, то Ku ≈ 1. Если Z2 = Z1, то Ku = 1/2. Включим в качестве Z2 последовательный колебательный контур. Учитывая форму частотной характеристики сопротивления контура и если взять R1 >> R2, то частотная характеристика делителя будет иметь форму, изображенную на рисунке. Такой фильтр называют фильтр пробка.
Вывод: последовательный колебательный контур может быть использован, как полосовой или режекторный фильтр.
Список рекомендуемой литературы
Основная литература
Дополнительная литература
План проведения практических занятий
План проведения лабораторных занятий
Задания для самостоятельной работы обучающихся
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.188.152 (0.005 с.) |

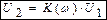
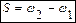
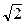 от максимального значения параметра
от максимального значения параметра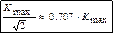

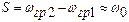 S << ω0
S << ω0