
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение схемы замещения трансформатораСодержание книги
Поиск на нашем сайте
- для первого контура.
- для второго контура.
Запишем уравнения для мгновенных комплексных величин.
Сгруппируем слагаемые следующим образом. Структура уравнений подсказывает структуру схемы цепи, в которой индуктивности контуров равны (L1 –M) и (L2 –M) соответственно, а элементом связи – индуктивность – M. Рассмотрим два одинаковых контура, т.е. R1 = R2 = R, C1 = C2 = C, L1 = L1 = L.
Преобразование формулы. Рассмотрим коэффициент передачи при ω ≈ ω0.
2)
3)
4)
5) Все преобразования подставим в формулу (1):
Лекция 10. Методы расчета индуктивно связанных цепей.
Расчёт, анализ, построение частотных характеристик связанных контуров.
АЧХ коэффициента передачи:
АЧХ – коэффициента передачи зависит от фактора связи А. Выделяют три степени связи: 1) 2) A = 1 - оптимальная; 3) A > 1 - сильная связь. Если ω = ω0, то а = 0. K (0) = K (ω0).
1) A<1 слабая связь, одногорбая кривая
3) A>1 сильная связь, - двугорбая характеристика. Экстремумы характеристики возникают факторах связи:
Нельзя увеличить фактор связи А так, чтобы провал в характеристике достигал уровня
Такая кривая получается при A = 2.41.
Лекция 11. Цепи при периодических несинусоидальных воздействиях. Несинусоидальные воздействия. Разложение в ряд фурье. Действующее, среднее значения и мощность периодического несинусоидального сигнала.
На практике к несинусоидальности напряжений и токов следует подходить двояко: в силовой электроэнергетике несинусоидальные токи обусловливают в общем случае дополнительные потери мощности, пульсации момента на валу двигателей, вызывают помехи в линиях связи; поэтому здесь необходимо «всеми силами» поддержание синусоидальных режимов; в цепях автоматики и связи, где несинусоидальные токи и напряжения лежат в основе принципа действия электротехнических устройств, задача наоборот заключается в их усилении и передаче с наименьшими искажениями. В общем случае характер изменения величин может быть периодическим, почти периодическим и непериодическим. В данном разделе будут рассматриваться цепи только с периодическими переменными. Периодическими несинусоидальными величинами называются переменные, изменяющиеся во времени по периодическому несинусоидальному закону. Причины возникновения несинусоидальных напряжений и токов могут быть обусловлены или несинусоидальностью источника питания или (и) наличием в цепи хотя бы одного нелинейного элемента. Кроме того, в основе появления несинусоидальных токов могут лежать элементы с периодически изменяющимися параметрами. В качестве примера на рис. 1,а представлена цепь с нелинейным резистором (НР), нелинейная вольт-амперная характеристика (ВАХ) которого обусловливает несинусоидальную форму тока i в цепи при синусоидальном напряжении u на ее входе (см. рис. 1,б).
Для характеристики несинусоидальных периодических переменных служат следующие величины и коэффициенты (приведены на примере периодического тока): Максимальное значение - Действующее значение - Среднее по модулю значение - Среднее за период значение (постоянная составляющая) - Коэффициент амплитуды (отношение максимального значения к действующему) - Коэффициент формы (отношение действующего значения к среднему по модулю) - Коэффициент искажений (отношение действующего значения первой гармоники к действующему значению переменной) - Коэффициент гармоник (отношение действующего значения высших гармонических к действующему значению первой гармоники) - Разложение периодических несинусоидальных кривых в ряд Фурье Из математики известно, что всякая периодическая функция
При разложении в ряд Фурье функция представляется следующим образом:
Здесь
В выражении (1)
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.239.0 (0.006 с.) |

 Запишем уравнения контуров по второму закону Кирхгофа для мгновенных значений токов в контурах. Если в первом контуре протекает ток i1, то на зажимах 2-ой катушки трансформатора будет возникать ЭДС взаимной индукции
Запишем уравнения контуров по второму закону Кирхгофа для мгновенных значений токов в контурах. Если в первом контуре протекает ток i1, то на зажимах 2-ой катушки трансформатора будет возникать ЭДС взаимной индукции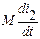 Если во втором контуре протекает i2, то на зажимах 1-ой катушки будет также возникать ЭДС взаимной индукции
Если во втором контуре протекает i2, то на зажимах 1-ой катушки будет также возникать ЭДС взаимной индукции

 Преобразуем уравнения: – в первом прибавим и вычтем
Преобразуем уравнения: – в первом прибавим и вычтем  ; во втором -
; во втором - 



 1)
1)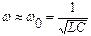
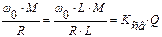





 А < 1 - слабая;
А < 1 - слабая;
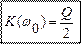 2) A=1 оптимальная связь, одногорбая кривая.
2) A=1 оптимальная связь, одногорбая кривая. a1=0,
a1=0,
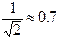
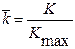 - нормированный коэффициент передачи.
- нормированный коэффициент передачи.
 .
. .
. .
.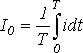 .
. .
. .
.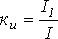 .
. .
. , где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверку на их выполнение проводить не нужно.
, где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверку на их выполнение проводить не нужно.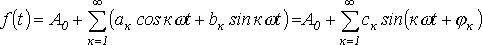
 - постоянная составляющая или нулевая гармоника;
- постоянная составляющая или нулевая гармоника;  - первая (основная) гармоника, изменяющаяся с угловой частотой
- первая (основная) гармоника, изменяющаяся с угловой частотой  , где Т – период несинусоидальной периодической функции.
, где Т – период несинусоидальной периодической функции. , где коэффициенты
, где коэффициенты 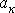 и
и  определяются по формулам
определяются по формулам




