
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центр тяжести плоской фигурыСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Если
БИЛЕТ38 38 тройной интэграл основные определения и свойства Определение. Пусть Как и в случае двойного интеграла, выполняются аналогичные свойства 1-6. Можно доказать, что если Вычисление тройного интеграла производится по следующему правилу. Теорема. Пусть Замечание. Если область Сформулируем общую теорему о замене переменных. Теорема. Пусть отображение БИЛЕТ39 39 вычисление тройного интэграла в декартовых координатах Рассмотрим случай, когда область интегрирования U является элементарной относительно оси O z, т.е. любая прямая, параллельная оси O z, пересекает границу области U не более, чем в двух точках. Пусть область U ограничена снизу поверхностью z = z 1(x,y), а сверху - поверхностью z = z 2(x,y) (рисунок 1). Проекцией тела U на плоскость O xy является область D (рисунок 2). Будем предполагать, что функции z 1(x,y) и z 2(x,y)непрерывны в области D.
Тогда для любой непрерывной в области U функции f (x,y,z) можно записать соотношение
Таким образом, вычисление тройного интеграла сводится к вычислению двойного интеграла, в котором подынтегральной функцией является однократный интеграл. В рассмотренном случае сначала вычисляется внутренний интеграл по переменной z, а затем - двойной интеграл в области D по переменным x и y. Если область D (x,y) является областью типа I (смотрите Повторные интегралы), т.е. ограничена линиями
где f 1(x), f 2(x) - непрерывные функции в интервале [ a,b ] и f 1(x) ≤ f 2(x), то, записывая двойной интеграл в виде повторного, получаем
В другом случае, когда область D (x,y) относится к типу II (является элементарной относительно оси O x) и ограничена линиями
где φ 1(y), φ 2(y) - непрерывные на отрезке [ c,d ] функции, причем φ 1(y) ≤ φ 2(y), тройной интеграл представляется в виде
Формулы (1) и (2) называются формулами сведения тройного интеграла к повторному. В частном случае, когда область интегрирования U представляет собой прямоугольный параллелепипед
Если исходная область интегрирования U более сложная, чем рассмотренная выше, то ее нужно разбить на конечное число более простых областей, в которых уже можно вычислить тройные интегралы методом сведения к повторным. БИЛЕТ40 40 замена переменных в тройном интэграле.цилиндрические координаты Пусть исходный тройной интеграл задан в декартовых координатах x, y, z в области U:
Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями:
Предполагается, что выполнены следующие условия: 1. Функции φ, ψ, χ непрерывны вместе со своими частными производными;
2. Существует взаимно-однозначное соответствие между точками области интегрирования U в пространстве xyz и точками области U' в пространстве uvw;
3. Якобиан преобразования I (u,v,w), равный
отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U. Тогда формула замены переменных в тройном интеграле записывается в виде:
В приведенном выражении Для вычисления тройных интегралов часто используются цилиндрические и сферические координаты. Эти случаи рассматриваются подробно на страницах
· В цилиндрических координатах положение точки M (x,y,z) в пространстве Oxyz определяется тремя числами − ρ, φ, z, где ρ − длина радиуса-вектора проекции точки M на плоскость Oxy, φ − угол, образованный этим радиусом-вектором с осью Ox (рисунок 1), z − проекция на ось Oz (ее значение одинаково в декартовых и цилиндрических координатах).
· Цилиндрические координаты точки связаны с ее декартовыми координатами соотношениями · · Здесь предполагается, что · · Якобиан перехода от декартовых координат к цилиндрическим равен · · Тогда формула замены переменных при данном преобразовании имеет вид: · · Переход к цилиндрическим координатам упрощает вычисление тройного интеграла в случаях, когда область интегрирования образована цилиндрической поверхностью. БИЛЕТ41 41 замена переменных в тройном интэграле.сферические координаты ρ − длина радиуса-вектора точки M;
Обратите внимание, что определения ρ, φ в сферических и цилиндрических координатах отличаются друг от друга. Сферические координаты точки связаны с ее декартовыми координатами соотношениями
Якобиан перехода от декартовых координат к сферическим имеет вид:
Раскладывая определитель по второму столбцу, получаем
Соответственно, абсолютное значение якобиана равно
Следовательно, формула замены переменных при преобразовании декартовых координат в сферические имеет вид:
Тройной интеграл удобнее вычислять в сферических координатах, когда область интегрирования U представляет собой шар (или некоторую его часть) и/или когда подынтегральное выражение имеет вид f (x 2 + y 2 + z 2). Иногда выгодно использовать т.н. обощенные сферические координаты, связанные с декартовыми формулами
В этом случае якобиан равен
БИЛЕТ42 42 приложения тройного интэграла
2. Вычисление массы тела переменной плотности γ (x; y; z):
3. Координаты центра тяжести тела с постоянной плотностью:
4. Координаты центра тяжести тела с переменной плотностью γ (x; y; z):
БИЛЕТ49 Пусть в области D заданы непрерывные функции P(x,y) и Q(х,y) и M0M - гладкая дуга, лежащая в области D. Рассмотрим вопрос о независимости интеграла
от формы пути интегрирования. Имеет место следующая теорема. Теорема 3.3. Пусть функции P, Q, P'y, Q'x определены и непрерывны в односвязной, ограниченной замкнутой области D плоскости Оху. Тогда следующие четыре условия равносильны между собой:
, где L - замкнутый контур в области D; 2) интеграл
не зависит от формы пути интегрирования, а зависит лишь от положения точек M0 и М;
в каждой точке области D. Идея доказательства этой теоремы: показывается, что из условия 1 Пример 3.7. Вычислить
, где контур L не охватывает начало координат. Решение
т. е. выполнено условие 4 теоремы. Значит выполнено и условие 1, т. е.
где L – любой контур, не охватывающий начало координат, так как в точке О(0,0) нарушаются условия теоремы, и её выводы в этом случае было бы нельзя применить. БИЛЕТ50. С помощью криволинейных интегралов вычисляются · Масса кривой; · Центр масс и моменты инерции кривой; · Работа при перемещении тела в силовом поле; · Магнитное поле вокруг проводника с током (Закон Ампера); · Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея). Рассмотрим эти приложения более подробно с примерами. Масса кривой Предположим, что кусок проволоки описывается некоторой пространственной кривой C. Пусть масса распределена вдоль этой кривой с плотностью ρ (x,y,z). Тогда общая масса кривой выражается через криволинейный интеграл первого рода
Если кривая C задана в параметрическом виде с помощью векторной функции
В случае плоской кривой, заданной в плоскости O xy, масса определяется как
или в параметрической форме
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 637; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.44.171 (0.007 с.) |

 , то координаты хc и уc центра С находятся так:
, то координаты хc и уc центра С находятся так:
 . Разбиение
. Разбиение  на части
на части  осуществляется непрерывными поверхностями. Диаметр разбиения определяется аналогично двумерному случаю. Также, по аналогии, можно определить для функции
осуществляется непрерывными поверхностями. Диаметр разбиения определяется аналогично двумерному случаю. Также, по аналогии, можно определить для функции  , разбиения
, разбиения 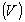 и выбранных точек
и выбранных точек  интегральную сумму
интегральную сумму  , где
, где  обозначает объем области
обозначает объем области  такое число, что
такое число, что 
 . Тогда мы говорим, что
. Тогда мы говорим, что 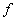 интегрируема на
интегрируема на  есть интеграл
есть интеграл  .
. ,
,  .
.  - квадрируемая область на плоскости,
- квадрируемая область на плоскости,  - непрерывные. Тогда
- непрерывные. Тогда 
 , где
, где  - непрерывные функции, то
- непрерывные функции, то 
 устанавливает взаимно однозначное соответствие между областями
устанавливает взаимно однозначное соответствие между областями  и
и  , причем функции
, причем функции  - непрерывно дифференцируемые и
- непрерывно дифференцируемые и  ни в одной точке
ни в одной точке  . Пусть
. Пусть 







 , тройной интеграл вычисляется по формуле
, тройной интеграл вычисляется по формуле




 означает абсолютное значение якобиана.
означает абсолютное значение якобиана.




 на плоскость Oxy и осью Ox;
на плоскость Oxy и осью Ox;






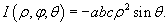







 условие 2
условие 2 



 , то ее масса описывается формулой
, то ее масса описывается формулой





