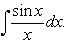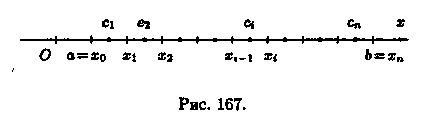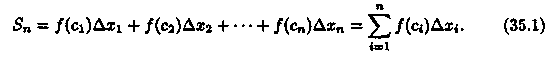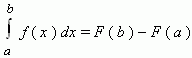Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Второй способ нахождения коэффициентовСодержание книги Поиск на нашем сайте
Второй способ нахождения искомых коэффициентов состоит в том, что в получаемом относительно БИЛЕТ4 Интегрирование тригонометрических функций I Рассмотрим интегралы вида
Такие интегралы всегда рационализируются подстановкой
Выразим далее переменную
Значит
Таким образом, задача свелась к вычислению интеграла от рациональной функции. Поскольку подстановка
БИЛЕТ5 5. Интегрирование иррациональных функций Пусть
Если заменить в
Этот интеграл рационализируется с помощью подстановки
В самом деле, так как подкоренное выражение представляет собой дробно-линейную относительно
Тогда
Замечание. Если под знаком интеграла содержатся корни с разными показателями, но с одним и тем же дробно-линейным относительно х подкоренным выражением, то сначала следует привести их к одному показателю, после чего использовать указанный прием.
БИЛЕТ6 6. Интегрирование диф. бинома (теорема Чебышёва) Дифференциальным биномом называют выражение вида
где a и b — любые константы, а показатели степеней m, n и p — рациональные числа. Изучим вопрос об интегрируемости в элементарных функциях дифференциальных биномов.
Подынтегральная функция в правой части является дробно-линейной иррациональностью следующего вида вида
3. Третьему случаю соответствует целому число
БИЛЕТ7 7.Специальные функции- функции которые выражаются через элементарные функции, представляются в виде рядов или интегралов. Интеграл неберущийся –если подынтегральная функция не является элементарной. Эти интегралы не выражают через элементарные функции, поэтому для них вычисляют вероятности для нормальной распределенной случайной величины этой функции. 3 метода вычислений:1приближенный метод Симсона 2.разложение подынтегральной функции в ряд Маклорена 3.с помощью таблицы значений функций Лапласа Примеры: 1.
БИЛЕТ8 8. Пусть функция у=ƒ(х) определена на отрезке [а; b], а < b. Выполним следующие действия. 1. С помощью точек х0=а, x1, х2,..., хn = В (х0 <x1 <...< хn) разобьем отрезок [а, b] на n частичных отрезков [х0;х1], [x1; х2],..., [хn-1,хn] (см. рис. 167).
2. В каждом частичном отрезке [xi-1;xi], i = 1,2,...,n выберем произвольную точку сi є [xi-1; xi] и вычислим значение функции в ней, т. е. величину ƒ(сi). 3. Умножим найденное значение функции ƒ (сi) на длину ∆xi=xi-xi-1 соответствующего частичного отрезка: ƒ (сi) • ∆хi. 4. Составим сумму Sn всех таких произведений:
Сумма вида (35.1) называется интегральной суммой функции у = ƒ(х) на отрезке [а; b]. Обозначим черезλ длину наибольшего частичного отрезка: λ = max ∆xi(i = 1,2,..., n). БИЛЕТ9 9. Физический смысл: 1) если задана скорость как функция от времени, то путь за время Т равен интегралу от скорости по времени; 2) если задано ускорение как функция от времени, то изменение скорости равно интегралу от ускорения по времени; Геометрический смысл: если функция y(x) больше нуля на промежутке [a;b], то площадь криволинейной трапеции, ограниченной графиком функции, осью ОХ и двумя прямыми х=а и х=b, равна интегралу от этой функции по переменной х на данном промежутке. БИЛЕТ10 10. Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x), вычислить ее значения в точках a и b и найти разность F(b) – F(a).
|
||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.76 (0.008 с.) |

 тождестве аргументу
тождестве аргументу 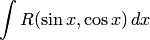 , где
, где 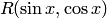 — рациональная функция.
— рациональная функция.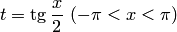 . В самом деле,
. В самом деле,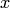 через переменную
через переменную 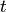 . Так как
. Так как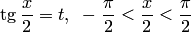 , то
, то 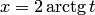 , а поэтому
, а поэтому 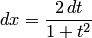 .
.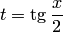 — позволяет рационализировать любой интеграл вида
— позволяет рационализировать любой интеграл вида 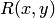 — рациональная функция от
— рациональная функция от  , т. е. функция, получаемая из
, т. е. функция, получаемая из  и чисел с помощью конечного числа арифметических операций (сложения, умножения и деления). Примерами таких функций могут служить
и чисел с помощью конечного числа арифметических операций (сложения, умножения и деления). Примерами таких функций могут служить , то получим функцию
, то получим функцию 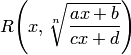 от одной переменной
от одной переменной 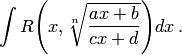
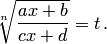
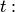
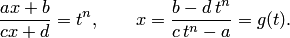
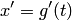 — рациональная функция. Заменяя теперь переменную в данном интеграле, получим интеграл от рациональной функции новой переменной
— рациональная функция. Заменяя теперь переменную в данном интеграле, получим интеграл от рациональной функции новой переменной 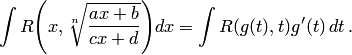
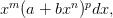
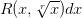 , где r — наименьшее общее кратное знаменателей рациональных чисел m и n. Стало быть, интеграл от дифференциального бинома в этом случае рационализируется подстановкой
, где r — наименьшее общее кратное знаменателей рациональных чисел m и n. Стало быть, интеграл от дифференциального бинома в этом случае рационализируется подстановкой 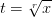 .
.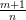 . Сделаем подстановку
. Сделаем подстановку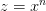 и положим для краткости
и положим для краткости 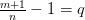 , получим
, получим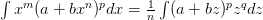
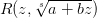 , где s — знаменатель рационального числа p.
, где s — знаменатель рационального числа p.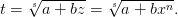
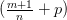 . Подынтегральная функция в правой части является дробно-линиейной иррациональностью вида
. Подынтегральная функция в правой части является дробно-линиейной иррациональностью вида 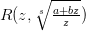 , так что интеграл от дифференциального бинома рационализируется подстановкой вида
, так что интеграл от дифференциального бинома рационализируется подстановкой вида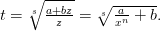
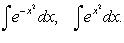 2.
2.  3.
3. 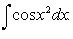 4.
4.