
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предельные признаки сравнения рядов
Пусть даны два ряда
Так называемый обобщенный гармонический ряд 32 Признак Даламбера Перед тем как сформулировать сам признак, рассмотрим важный вопрос: Сначала начнем с повторения. Вспомним случаи, когда нужно применять самый ходовой предельный признак сравнения. Предельный признак сравнения применяется тогда, когда в общем члене ряда: Основные же предпосылки для применения признака Даламбера следующие: 1) В общий член ряда («начинку» ряда) входит какое-нибудь число в степени, например, 2) В общий член ряда входит факториал. С факториалами мы скрестили шпаги ещё на уроке Числовая последовательность и её предел. Впрочем, не помешает снова раскинуть скатерть-самобранку: ! При использовании признака Даламбера нам как раз придется расписывать факториал подробно. Как и в предыдущем пункте, факториал может располагаться вверху или внизу дроби. 3) Если в общем члене ряда есть «цепочка множителей», например, Вместе со степенями или (и) факториалами в начинке ряда часто встречаются многочлены, это не меняет дела – нужно использовать признак Даламбера. Кроме того, в общем члене ряда может встретиться одновременно и степень и факториал; может встретиться два факториала, две степени, важно чтобы там находилось хоть что-то из рассмотренных пунктов – и это как раз предпосылка для использования признака Даламбера. Признак Даламбера: Рассмотрим положительный числовой ряд
Признак Коши Радикальный признак Коши — признак сходимости числового ряда:
Условие радикального признака равносильно следующему:
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
Доказательство 1. Пусть
Раскрыв модуль, получаем:
Поскольку 2. Пусть
Раскрыв модуль, получаем:
Поскольку
33Интегральный признак
Определить, сходится или расходится ряд Решение. Вычислим соответствующий несобственный интеграл:
Таким образом, данный ряд расходится. 34 Знакочередующиеся ряды Что такое знакочередующийся ряд? Это понятно или почти понятно уже из самого названия. Сразу простейший пример. Рассмотрим ряд
А сейчас будет убийственный комментарий. У членов знакочередующегося ряда чередуются знаки: плюс, минус, плюс, минус, плюс, минус и т.д. до бесконечности.
Знакочередование обеспечивает множитель В практических примерах знакочередование членов ряда может обеспечивать не только множитель
Подводным камнем являются «обманки»: Как исследовать знакочередующийся ряд на сходимость? Использовать признак Лейбница. Про немецкого гиганта мысли Готфрида Вильгельма Лейбница я рассказывать ничего не хочу, так как помимо математических трудов, он накатал несколько томов по философии. Опасно для мозга. Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится. Или в два пункта: 1) Ряд является знакочередующимся. 2) Члены ряда убывают по модулю: Если выполнены оба условия, то ряд сходится. Что значит «по модулю»? Модуль, как мы помним со школы, «съедает» знак «минус». Вернемся к ряду – Члены ряда без учёта знака убывают. Конец справки Теперь немного поговорим про монотонность. Монотонность – это скучное постоянство. Члены ряда строго монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю МЕНЬШЕ, чем предыдущий: Члены ряда нестрого монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю НЕ БОЛЬШЕ предыдущего: В условиях теоремы Лейбница должна выполняться монотонность убывания (неважно, строгая или нестрогая). При этом члены ряда могут даже некоторое время возрастать по модулю, но «хвост» ряда обязательно должен быть монотонно убывающим. Абсолютная и условная сходимость числового ряда. Признак Лейбница Для знакочередующихся рядом действует достаточный признак сходимости Лейбница. 1. an +1 < an для всех n; 2. Тогда знакочередующиеся ряды
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.243.41 (0.011 с.) |
 и
и  , у которых члены an и bn положительны для всех n. Тогда справедливы следующие предельные признаки:
, у которых члены an и bn положительны для всех n. Тогда справедливы следующие предельные признаки: , то оба ряда
, то оба ряда 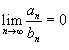 , то ряд
, то ряд  , то ряд
, то ряд  сходится при p > 1 и расходится при 0 < p ≤ 1.
сходится при p > 1 и расходится при 0 < p ≤ 1. ,
, 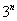 ,
,  и так далее. Причем, совершенно не важно, где эта штуковина располагается, в числителе или в знаменателе – важно, что она там присутствует.
и так далее. Причем, совершенно не важно, где эта штуковина располагается, в числителе или в знаменателе – важно, что она там присутствует.
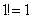
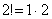




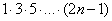 . Этот случай встречается редко, но! При исследовании такого ряда часто допускают ошибку – см. Пример 6.
. Этот случай встречается редко, но! При исследовании такого ряда часто допускают ошибку – см. Пример 6. . Если существует предел отношения последующего члена к предыдущему:
. Если существует предел отношения последующего члена к предыдущему:  , то:
, то: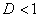 ряд сходится. В частности, ряд сходится при
ряд сходится. В частности, ряд сходится при 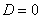 .
.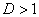 ряд расходится. В частности, ряд расходится при
ряд расходится. В частности, ряд расходится при 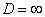 .
.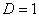 признак не дает ответа. Нужно использовать другой признак. Чаще всего единица получается в том случае, когда признак Даламбера пытаются применить там, где нужно использовать предельный признак сравнения.
признак не дает ответа. Нужно использовать другой признак. Чаще всего единица получается в том случае, когда признак Даламбера пытаются применить там, где нужно использовать предельный признак сравнения.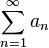 с неотрицательными членами существует такое число
с неотрицательными членами существует такое число 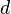 ,
, 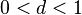 , что, начиная с некоторого номера, выполняется неравенство
, что, начиная с некоторого номера, выполняется неравенство  , то данный ряд сходится.
, то данный ряд сходится.
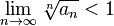
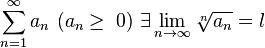 , то
если
, то
если 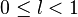 ряд сходится,
если
ряд сходится,
если  ряд расходится,
если
ряд расходится,
если 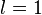 вопрос о сходимости ряда остается открытым.
вопрос о сходимости ряда остается открытым.
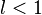 . Очевидно, что существует такое
. Очевидно, что существует такое 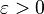 , что
, что  . Поскольку существует предел
. Поскольку существует предел 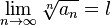 , то, подставив в определение предела выбранное
, то, подставив в определение предела выбранное  , получим:
, получим: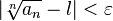
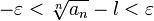
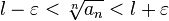
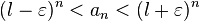
 сходится. Следовательно, по признаку сравнения ряд
сходится. Следовательно, по признаку сравнения ряд 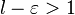 . Поскольку существует предел
. Поскольку существует предел 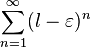 расходится. Следовательно, по признаку сравнения ряд
расходится. Следовательно, по признаку сравнения ряд 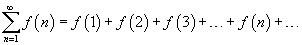 сходится, если сходится несобственный интеграл
сходится, если сходится несобственный интеграл  , и расходится, если
, и расходится, если  .
.
 .
Решение.
Используем интегральный признак Коши. Вычислим соответствующий несобственный интеграл:
.
Решение.
Используем интегральный признак Коши. Вычислим соответствующий несобственный интеграл:
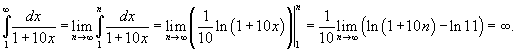 Таким образом, данный ряд расходится.
Таким образом, данный ряд расходится.
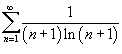 .
.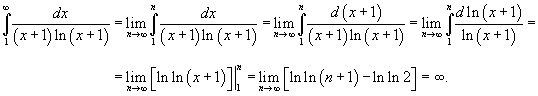
 и распишем его подробнее:
и распишем его подробнее:
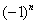 : если
: если 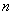 чётное, то будет знак «плюс», если нечётное – знак «минус» (как вы помните ещё с урока о числовых последовательностях, эта штуковина называется «мигалкой»). Таким образом, знакочередующийся ряд «опознается» по минус единичке в степени «эн».
чётное, то будет знак «плюс», если нечётное – знак «минус» (как вы помните ещё с урока о числовых последовательностях, эта штуковина называется «мигалкой»). Таким образом, знакочередующийся ряд «опознается» по минус единичке в степени «эн».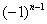 ,
, 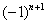 ,
, 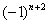 , …. Например:
, …. Например: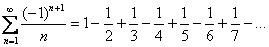
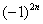 ,
, 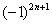 ,
, 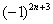 и т.п. – такие множители не обеспечивают смену знака. Совершенно понятно, что при любом натуральном
и т.п. – такие множители не обеспечивают смену знака. Совершенно понятно, что при любом натуральном 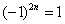 ,
, 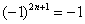 ,
,  . Ряды с обманками подсовывают не только особо одаренным студентам, они время от времени возникают «сами собой» в ходе решения функциональных рядов.
. Ряды с обманками подсовывают не только особо одаренным студентам, они время от времени возникают «сами собой» в ходе решения функциональных рядов.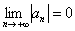 . Причём, убывают монотонно.
. Причём, убывают монотонно.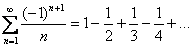 . Мысленно сотрём ластиком все знаки и посмотрим на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий. Таким образом, следующие фразы обозначают одно и то же:
. Мысленно сотрём ластиком все знаки и посмотрим на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий. Таким образом, следующие фразы обозначают одно и то же: . Для ряда
. Для ряда 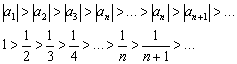
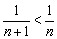 .
.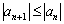 . Рассмотрим ряд с факториалом:
. Рассмотрим ряд с факториалом: 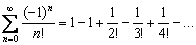 Здесь имеет место нестрогая монотонность, так как первые два члена ряда одинаковы по модулю. То есть, каждый следующий член ряда по модулю не больше предыдущего:
Здесь имеет место нестрогая монотонность, так как первые два члена ряда одинаковы по модулю. То есть, каждый следующий член ряда по модулю не больше предыдущего:  .
. .
.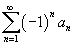 и
и 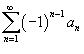 сходятся.
сходятся.


