
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточное условие экстремума ФНП, критерий СильвестраСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть функция Рассмотрим случай двух переменных. Пусть функция
Тогда на основе вышесказанного и критерия Сильвестра знакоопределенности квадратичной формы,, следуют такие выводы: 1) если 2) если 3) если Теорема 2 (достаточные условия экстремума). Пусть в некоторой окрестности точки М0 (х0, у0), являющейся стационарной точкой функции Z = F (X, Y), эта функция имеет непрерывные частные производные до 3-го порядка включительно. Обозначим
Тогда: 1) F (X, Y) имеет в точке М0 максимум, если AC – B ² > 0, A < 0; 2) F (X, Y) имеет в точке М0 минимум, если AC – B ² > 0, A > 0; 3) экстремум в стационарной точке отсутствует, если AC – B ² < 0; 4) если AC – B ² = 0, необходимо дополнительное исследование . Доказательство. Напишем формулу Тейлора второго порядка для функции F (X, Y), помня о том, что в стационарной точке частные производные первого порядка равны нулю:
Если угол между отрезком М0М, где М (х0+ D Х, у0+ D У), и осью О Х обозначить J, то D Х = D R cos J, D Y = D R Sin J. При этом формула Тейлора примет вид:
Пусть
Достаточное условие экстремума 1) Первое достаточное условие: Если: а) f(x) непрерывная функция и определена в некоторой окрестности точки такой, что первая производная в данной точке равна нулю или не существует. б) f(x) имеет конечную производную в окрестности задания и непрерывности функции в) производная сохраняет определенный знак справа от точки и слева от этой же точки, тогда точку можно охарактеризовать следующим образом Это условие не очень удобное, так как нужно проверять множество условий и запоминать таблицу, однако если ничего не сказано о производных высших порядках, то это единственный способ найти экстремум функции. 2) Второе достаточное условие Если функция g(x) обладает второй производной 3) Третье достаточное условие Пусть функция g(x) имеет в некоторой окрестности точки N производных, причем значение первых (N - 1)- ой и самой функции в этой точке равно нулю, а значение N-ой производной отлично от нуля. В таком случае: а) Если N - четно, то точка экстремум функции: б) Если N - нечетно, то в точке у функции g(x) экстремуманет. Критерий Сильвестра: Пусть квадратичная форма записана в виде матрицы
Эта форма является положительно определенной тогда и только тогда, когда все его главные миноры положительны.
Форма является отрицательно определенной, если ее главные миноры имеют чередующиеся знаки, начиная с отрицательного:
Задача: Исследовать функцию многих переменных Необходимое условие экстремума. Необходимым условием экстремума функции является равенство нулю первых частных производных (все то же самое, что и для случая двух переменных, только уравнений в системе столько же, сколько переменных в функции). Точки
называются стационарными точками функции F.
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.008 с.) |

 дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки  и дважды дифференцируема в самой точке
и дважды дифференцируема в самой точке  , причем точка
, причем точка  – точка возможного экстремума данной функции, т. е.
– точка возможного экстремума данной функции, т. е.  . Тогда если второй дифференциал
. Тогда если второй дифференциал  является положительно определенной (отрицательно определенной) квадратичной формой от переменных
является положительно определенной (отрицательно определенной) квадратичной формой от переменных 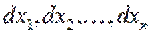 , то функция
, то функция  имеет в точке
имеет в точке  локальный минимум(максимум). Если же
локальный минимум(максимум). Если же  является знакопеременной квадратичной формой, то в точке
является знакопеременной квадратичной формой, то в точке  функция не имеет локального экстремума.
функция не имеет локального экстремума. дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки  и дважды дифференцируема в самой точке
и дважды дифференцируема в самой точке  , причем точка
, причем точка  . Введем обозначения:
. Введем обозначения: .
. , то в точке
, то в точке 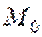 функция
функция  имеет локальный экстремум, причем максимум, если
имеет локальный экстремум, причем максимум, если  и минимум, если
и минимум, если  ;
; , то в точке
, то в точке  функция
функция  не имеет локального экстремума;
не имеет локального экстремума;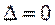 , то в точке
, то в точке 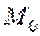 функция
функция  может иметь локальный экстремум, а может и не иметь его.
может иметь локальный экстремум, а может и не иметь его.


 Тогда можно разделить и умножить выражение в скобках на А. Получим:
Тогда можно разделить и умножить выражение в скобках на А. Получим:



 причем в некоторой точке первая производная равна нулю, а вторая производная отлично от нуля. Тогда точка экстремум функции g(x), причем если
причем в некоторой точке первая производная равна нулю, а вторая производная отлично от нуля. Тогда точка экстремум функции g(x), причем если  , то точка является максимумом; если
, то точка является максимумом; если  , то точка является минимумом.
, то точка является минимумом. у функции точка максимума,
у функции точка максимума,  у функции точка минимума.
у функции точка минимума.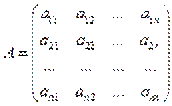

 .
. на экстремум и вычислить экстремальное значение функции. Решение:
на экстремум и вычислить экстремальное значение функции. Решение: , являющиеся решением системы:
, являющиеся решением системы:



