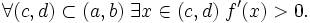Монотонная функция. Условие монотонности функций.

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда отрицательная, либо всегда положительная. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

 

Функция возрастает, если большему значению аргумента соответствует большее значение функции. • Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

Условия монотонности функции:

(Критерий монотонности функции, имеющей производную на интервале) Пусть функция

непрерывна на (a,b), и имеет в каждой точке

 

производную f'(x). Тогда

f возрастает на (a,b) тогда и только тогда, когда

 

 

f убывает на (a,b) тогда и только тогда, когда

 

 

Достаточное условие другой монотонности функции, имеющей производную на интервале) Пусть функция

непрерывна на (a,b), и имеет в каждой

 

 

производную f'(x). Тогда

 

если

 

то f строго возрастает на (a,b);

 

если

то f строго убывает на (a,b).

 

 

Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале (a,b). Точнее имеет место

(Критерий строгой монотонности функции, имеющей производную на интервале) Пусть

 

 

и всюду на интервале определена производная f'(x). Тогда f строго возрастает на интервале (a,b) тогда и только тогда, когда выполнены следующие два условия:

 

 

 

Аналогично, f строго убывает на интервале (a,b) тогда и только тогда, когда выполнены следующие два условия:

 

 

 

 

24. Экстремум функции. Необходимое условие экстремума (теорема Ферма). Достаточное условие экстремума.

 

Достаточное условие возрастания (убывания) функции на промежутке. Понятие экстремума функции. Необходимое условие экстремума функции (теорема Ферма).

Если производная некоторой непрерывной функции f(x) на некотором промежутке положительна (f'(x)>0), то на этом промежутке функция возрастает.

 

Если производная некоторой непрерывной функции f(x) на некотором промежутке отрицательна (f'(x)<0), то на этом промежутке функция убывает.

 

Эти условия являются достаточными условиями возрастания (убывания функции).

Постараемся понять, почему так происходит (строгое доказательство рассматривается в программе высших учебных заведений). Известно, что геометрический смысл производной - тангенс угла наклона касательной. Значит, если производная положительна, то угол будет острым.

 

И получается, что график идет «в гору». Если производная отрицательна, то угол наклона будет тупым и получается, что график идет «под гору».

 

 

 

Промежутки возрастания и убывания называют промежутками монотонности функции.

Точка x0 называется точкой максимума функции f(x), если существует положительное число E, такое, что для любой точки x из промежутка

 

 

 

, выполняется неравенство

 

 

Иными словами, значение функции f(x0) самое большое в некоторой окрестности точки x0.

 

Точка x0 называется точкой минимума функции f(x), если существует положительное число E, такое, что для любой точки x из промежутка

 

 

выполняется неравенство

Иными словами значение функции f(x0) самое маленькое в некоторой окрестности точки x0.

 

На следующем графике точки -9 и 3 являются точками максимума, а точка -2 является точкой минимума.

 

 

 

 

Точки максимума или минимума называются точками экстремума.

 

Теорема Ферма: Если x0 - точка экстремума непрерывной функции f(x), то f'(x0)=0.

 

Геометрически это выглядит так: в точке экстремума касательная параллельна оси ОХ и, поэтому угол наклона равен 0.

 

Это условие является необходимым, но не достаточным условием экстремума.