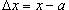Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рассмотрим односторонние пределыСодержание книги
Поиск на нашем сайте
Пусть
Отложим этот угол на единичной окружности (R = 1).
Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.
Очевидно, что:
(где SsectOKA — площадь сектора OKA)
(из
: | LA | = tgx) Подставляя в (1), получим:
Так как при
Умножаем на sinx:
Перейдём к пределу:
Найдём левый односторонний предел:
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия:
Понятие непрерывности функций. Непрерывность элементарных функций. Основные свойства непрерывных функций: существование наименьших и наибольших значений, существование промежуточных значений. Примеры разрывных функций. Непрерывная функция — функция без «скачков», то есть такая у которой малые изменения аргумента приводят к малым изменениям значения отображения.
Непрерывная функция вообще говоря, — синоним понятия непрерывное отображение, тем не менее, чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающих вещественные значения.
Определение непрерывности по Гейне Говорят, что функция действительного переменного f (x) является непрерывной в точке
(
множество действительных чисел), если для любой последовательности
такой, что
выполняется соотношение
На практике удобно использовать следующие 3 условия непрерывности функции f (x) в точке x = a:
Функция f (x) определена в точке x = a; 2. Предел
3. Выполняется равенство
Определение непрерывности по Коши (нотация
Рассмотрим функцию f (x), которая отображает множество действительных чисел
на другое подмножество B действительных чисел. Говорят, что функция f (x) является непрерывной в точке
если для любого числа
существует число
такое, что для всех
удовлетворяющих соотношению
выполняется неравенство
Определение непрерывности в терминах приращений аргумента и функции Определение непрерывности можно также сформулировать, используя приращения аргумента и функции. Функция является непрерывной в точке x = a, если справедливо равенство
где
Приведенные определения непрерывности функции эквивалентны на множестве действительных чисел.
Функция является непрерывной на данном интервале, если она непрерывна в каждой точке этого интервала.
Асимптоты графика функции. Асимптоты графика функции Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные. Определение 7. 1 Вертикальной асимптотой графика функции
называется вертикальная прямая
, если
или
при каком -либо из условий
Заметим, что мы при этом не требуем, чтобы точка принадлежала области определения функции
однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки:
или
где
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.113.135 (0.005 с.) |

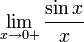


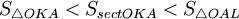




















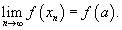
 существует;
существует;