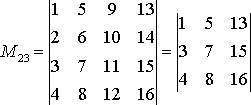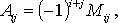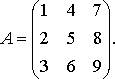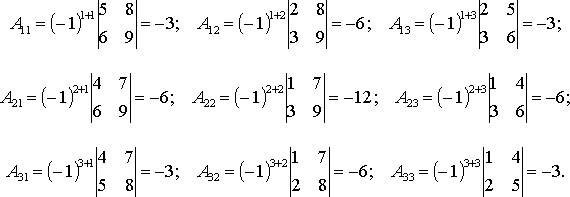Определители квадратных матриц. Миноры и алгебраические дополнения элементов квадратных матриц. Вычисление определителей. Свойства определителей.

Определители 2-го и 3-го порядков.

 

Будем рассматривать квадратные матрицы

 

Определители являются основными числовыми характеристиками квадратных матриц.

Определителем (детерминантом) матрицы,

 

состоящей из одного числа, называется само это число.

Определителем матрицы А= второго порядка называется число, равное разности произведений элементов главной и побочной диагоналей:

 

Рассмотрим матрицу третьего порядка:

Определителем матрицы A третьего порядка называется число

Минором элемента матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-й строки и j-го столбца.

 

 

ри выписывании определителя (n-1)-го порядка, в исходном определителе элементы находящиеся под линиями в расчет не принимаются.

 

Пример 1. Составить минор, полученную из исходной матрицы:

Решение

Алгебраические дополнения

 

Алгебраическим дополнением Аij элемента аij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:

 

 

то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.

 

Пример 1. Найти алгебраические дополнения всех элементов матрицы

Решение

Обратная матрица.

Обра́тная ма́трица — такая матрица A-1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

 

 

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Свойства обратной матрицы.

, где det обозначает определитель.

(AB) − 1 = B − 1A − 1 для любых двух обратимых матриц A и B.

(AT) − 1 = (A − 1)T где * T обозначает транспонированную матрицу.

(kA) − 1 = k − 1A − 1 для любого коэффициента.

Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A - 1 существует, то x = A − 1b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

 

Системы линейных уравнений. Основные понятия.

Многие теоретические и практические вопросы приводят не к одному уравнению, а к целой системе уравнений с несколькими неизвестными. Особенно важен случай системы линейных уравнений, т.е. системы m уравнений 1ой степени с n неизвестными:

 

a11x1 + … + a1n xn = b1;

 

a21x1 + … + a2n x n = b2;

 

………………………………

 

am1x1+ … + amnxn = bm.

 

Здесь x1, …, xn - неизвестные, а коэффициенты записаны так, что индексы при них указывают на номер уравнения и номер неизвестного. Значение систем 1-й степени определяется не только тем, что они простейшие. На практике часто имеют дело с заведомо малыми величинами, старшими степенями которых можно пренебречь, так что уравнения с такими величинами сводятся в первом приближении к линейным. Не менее важно, что решение систем линейных уравнений составляет существенную часть при численном решении разнообразных прикладных задач.

 

Способы решения систем линейных уравнений - очень интересная и важная тема. Системы уравнений и методы их решения рассматриваются в школьном курсе математики, но недостаточно широко. А для того, чтобы перейти к исследованию данной темы, также нужно было познакомиться с темой матриц и определителей. Этот же материал вообще в школьной программе не изучается. В процессе знакомства с данной работой приобретаются навыки, с помощью которых в последующем решение систем линейных уравнений станет намного проще, понятнее и быстрее.

 

6. Решение системы из п уравнений с п неизвестными по формуле Крамера и методом обратной матрицы.

a11x1 + a12x2 + …+ a1n xn = b1;

 

a21x1 + a22x2 + …+ a2n xn = b2; (2)

 

……………………………………

 

an1x1 + an2x2 + …+ annxn = bn;

 

Определителем системы (2) называется определитель, составленный из коэффициентов аij.

 

a11 a12 … a1n

 

? = a21 a22 … a2n

 

…………………………

 

an1 an2 … ann

Рассмотрим случай, когда?? 0. Докажем, что в этом случае система (2) является определенной, т.е. имеет одно единственное решение. Как и ранее, через Аij будем обозначать алгебраическое дополнение элемента аij в определителе?.

 

Умножим каждое уравнение системы (2) на алгебраические дополнения элементов i-го столбца определителя?, т.е. первое уравнение умножим на А1i, второе - на А2i и т.д., наконец, последнее уравнение - на Аni, а затем все полученные уравнения системы сложим. В результате будем иметь

 

(a11x1 + a12x2 + …+ a1ixi + …+ a1nxn) A1i + (a21x1 + a22x2 + …+ a2ixi +

+ …+ a2nxn) A2i + …+ (an1x1 + an2x2 + …+ anixi + …+ anxnn) Ani = b1A1i + b2A2i + …+ bnAni

 

 

или, сгруппировав члены относительно известных x1, x2, …, xn, получим

 

(a11A1i + a21A2i + …+ an1Ani) x1 + … +

 

 

+ (a1iA1i + a2iA2i + …+ aniAni) xi + … +

 

+ (a1nA1i + a2nA2i + …+ annAni) xn =

 

= b1A1i + b2A2i + …+ bnAni. (3)

 

Коэффициент при неизвестной хi равен определителю?, а коэффициенты при всех других неизвестных равны нулю. Свободный член уравнения (3) отличается от коэффициента при х1 тем, что коэффициенты а1i, а2i, …, аni заменены свободными членами b1, b2, …, bn уравнения (2). Следовательно, выражение b1A1i + b2A2i + …+ bnAni есть определитель i-го порядка, отличающийся от определителя только i-м столбцом, который заменен столбцом свободных членов. Обозначив этот определитель?xi, будем иметь

a11 a12 … b1 … a1n

?xi = a21 a22 … b2 … a2n. (3)

………………………………

an1 an2 … bn … ann

Таким образом, уравнение (3) можно записать в виде

?х =?xi,

откуда при?? 0

х = ----

Придавая индексу i значения 1, 2, …, n, получаем:

х1 = ----;

х2 = ----;

(4)

………………

хn = ----.

Рассмотренный метод решения системы уравнений называется правилом Крамера, а формулы (4) - формулами Крамера.

 

 

Метод Гаусса.

Практическое значение правила Крамера для решения системы n линейных уравнений с п неизвестными невелико, так как при его применении приходится вычислять п +1 определителей n-го порядка:, x1, x2, …,xn. Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.

Итак, пусть дана система, содержащая m линейных уравнений с п неизвестными:

а11х1 + а12х2 + …+ а1nхn = b1;

а21х1 + а22х2 + …+ а2nхn = b2; (6)

. ……………………………………

аm1х1 + аm2х2 + …+ аmnхn = bm

Требуется найти все решения системы уравнений (6). Будем производить над системой элементарные преобразования: исключение из системы уравнения вида

 

0х1 + 0х2 + …+ 0хn = 0 (7)

 

и прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое число.

 

Очевидно, что если мы проделаем над уравнениями системы (6) любое из приведенных выше преобразований, то получим систему, равносильную исходной. При необходимости систему (6) будем подвергать еще одному виду преобразований - перенумерации переменных и уравнений. Идея этого преобразования заключается в следующем. Если, например, возникает необходимость, чтобы в каком-то уравнении системы (например, в k -м) неизвестная x1 стояла на первом месте, то в результате перенумерации соответствующее уравнение запишется в виде

 

akix1 +... + ak2x2 + … + ak1xi+... + aknxn = bk,

 

 

т. е. вместо прежней неизвестной хi мы будем писать х1, а вместо x1 - хi Метод Гаусса решения системы (6) заключается в последовательном исключении переменных.

 

Если среди уравнений системы есть хотя бы одно уравнение вида

 

0xl + 0x2+... + 0xn= b, (8)

 

причем b 0, то совершенно очевидно, что ни одна система значений х1, х2..., хп не удовлетворяет этому уравнению, а следовательно, и системе в целом, поэтому система несовместна.

 

Пусть теперь система (6) не содержит уравнений вида (7) или (8). Это значит, что в каждом уравнении системы хотя бы один из коэффициентов отличен от нуля. Пусть a110 (в противном случае, применив элементарные преобразования, мы сможем добиться, чтобы первый коэффициент первого уравнения был отличен от нуля). Оставив первое уравнение без изменения, исключим из всех уравнений системы (6), начиная со второго, неизвестную х1. Для этого из второго уравнения вычтем первое, умноженное на a21/a11, затем из третьего уравнения вычтем также первое, но уже умноженное на a31/a11, и так до последнего уравнения. В результате этих преобразований мы получим равносильную систему

 

а11х1 + а12х2 + … + а1nхn = b1;

 

а?22х2 + …+ а?2nхn = b?2;

 

………………………… (9)

 

а?m2х2 + …+ а?mnхn = b?m

 

 

Заметим, что в системе (9) число уравнений может быть и меньше m, так как среди них могут оказаться уравнения вида (7), которые, как мы условились ранее, можно отбросить.

 

Пусть а22 0. Применим те же самые рассуждения и исключим из последних п - 2 уравнений системы (9) неизвестную х2 путем вычитания из третьего уравнения второго, умноженного на a?32/a?22, из четвертого уравнения -- второго, умноженного на a?34/a?22 и т. д. В результате получим систему

 

а11х1 + а12х2 + а13х3 + …+ а1nхn = b1;

 

а?22х2 + а?23х3 + …+ а?2nхn = b?2;

а?22х2 + а?23х3 + …+ а?2nхn = b?2;

 

а??33х3 + …+ а?3хn = b?3;

 

……………………………

 

а?m3х3 +…+а?mnхn = b?m

 

.

 

Продолжая этот процесс, систему (6) приведем к равносильной системе вида

 

c11х1 + c12х2 + c13х3 + …+ c1kхk + …+ c1nхn = d1;

 

c22х2 + c23х3 + …+ c2kхk + …+ c2nхn = d2;

 

c33х3 + …+ c3kхk + …+ c3nхn = d3; (10)

 

………………………………………

 

ckkхk + …+cknхn = dk.

 

в которой коэффициенты c11, c22,..., ckk отличны от нуля.

 

Может оказаться, что в процессе преобразования на каком-то шаге в полученной системе окажется уравнение вида (8). В этом случае система (7) не имеет решений. Предположим теперь, что среди уравнений полученной системы нет уравнения вида (8). Тогда для решения системы (6) необходимо решить систему (9), что не составляет особого труда. Рассмотрим два возможных случая.

 

1. k = n (это частный случай, когда число уравнений совпадает с числом неизвестных). Тогда последнее уравнение системы (10) имеет вид сппхп = dn, откуда хп = dn /cnn. Подставив это значение в предпоследнее уравнение системы (7), имеющее вид

 

cn-1n-1xn-1 + cn-1nxn= dn-1, найдем значение неизвестной xn-1 и т. д.; наконец, из первого уравнения найдем неизвестную x1 Таким образом, в случае k = п система уравнений (6) имеет единственное решение.

 

2. k < n. Тогда из последнего уравнения системы (10), найдем неизвестную xk, выраженную через неизвестные хk+1, хk+2,... xn:

 

xk = (dkk - ck k+1xk+1 - … - cknxn)

Подставив это значение неизвестной в предпоследнее уравнение системы (10), найдем выражение для неизвестной хk-1,и т. д.; наконец, подставив значения неизвестных хk, хk-1,... x2 в первое уравнение системы (10), получим выражение для неизвестной x1. В результате указанная система уравнений (6) приводится к виду

 

x1 = d?1 + c?1 k+1xk+1 + …+ c?1nxn;

 

x2 = d?2 + c?2 k+1xk+1 + …+ c?2nxn; (11)

 

………………………………………

 

xk = d?k + c?k k+1 xk+1 + …+ cknxn.

 

 

Неизвестные хk+1, хk+2, …, хп называются свободными. Им можно придать различные значения и затем из системы (6) найти значения неизвестных х1, х2, …, хk. Таким образом, в случае k < п совместная система уравнений (6) имеет бесчисленное множество решений.

 

Заметим, что если в процессе приведения системы (6) к системе (11) была произведена перенумерация неизвестных, то в системе (11) необходимо вернуться к их первоначальной нумерации.

 

На практике процесс решения системы уравнений облегчается тем, что указанным выше преобразованиям подвергают не саму систему, а матрицу, составленную из коэффициентов уравнений системы (6) и их свободных членов. При этом каждому элементарному преобразованию, проведенному над системой (6), соответствует преобразование над матрицей (12): вычеркивание строки, все элементы которой состоят из нулей, прибавление к элементам некоторой строки соответствующих элементов другой строки, умноженных на некоторое число, и перестановка двух столбцов матрицы (12).

 

Пример 1. Решить методом Гаусса систему уравнений

x1 - 2x2 + x3 + x4 = -1;

 

3x1 + 2x2 - 3x3 - 4x4 = 2;

 

2x1 - x2 + 2x3 - 3x4 = 9;

 

x1 + 3x2 - 3x3 - x4 = -1